Digitale Werkzeuge in der Schule/Rund ums Dreieck/Besondere Dreiecke

Info

In diesem Lernpfadkapitel entdeckst du, wie du Dreiecke vergleichen kannst. Dabei lernst du die verschiedenen Dreiecksarten kennen.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

 

Teste dein Vorwissen

Aufgabe 1: Winkelarten

Erinnerst du dich noch an die verschiedenen Winkelarten? Teste dein Vorwissen mithilfe der folgenden Aufgabe.

Je nach der Weite des Winkels werden Winkel in verschiedene Kategorien eingeteilt. Ordne die Winkel der entsprechenden Kategorie zu.

Info

Solltest du dich nicht an die verschiedenen Winkelarten erinnern können, kannst du dir die Winkelarten im folgenden Merksatz noch einmal anschauen.

 

Erinnerung: Winkelarten

Man unterscheidet Winkel nach ihrer Größe:

• spitzer Winkel: kleiner als 90° (0° < a < 90°)
• rechter Winkel: exakt 90° (a = 90°)
• stumpfer Winkel: zwischen 90° und 180° (90° < a < 180°)
• überstumpfer Winkel: über 180° (180° < a < 360°)

Erkundung von Dreiecken

Aufgabe 2: Erkundung von Dreiecken

In der Abbildung siehst du verschiedene Dreiecke. Tim hat bei den Dreiecken schon eine Gemeinsamkeit entdeckt. Findest du weitere?

zurück zum Arbeitsblatt

Gib Dreiecke an die Gemeinsamkeiten haben und beschreibe diese Gemeinsamkeiten in wenigen Sätzen auf deinem Arbeitsblatt. (Hinweis: Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form)

Datei:Tim entdeckt rechte Winkel.jpg

Du kannst Dreiecke vergleichen, indem du ihre Winkel oder ihre Seitenlängen vergleichst.

Charakterisierungen von Dreiecken

Unterscheidung von Dreiecken mit Winkeln

Aufgabe 3: Unterscheidung von Dreiecken mithilfe von Winkeln

Finde durch Verschieben des Punktes alle Arten von Dreiecken heraus.

zurück zum Arbeitsblatt

Notiere dir ihre Eigenschaften auf deinem Arbeitsblatt.

Merksatz: Unterscheidung von Dreiecken mithilfe von Winkeln

Fülle den folgenden Merksatz aus.

Ein spitzwinkliges Dreieck hat drei spitze Winkel (<90°). Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel. Ein rechtwinkliges Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel.

zurück zum Arbeitsblatt

Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt.

Unterscheidung von Dreiecken mit Seitenlängen

Aufgabe 4: Unterscheidung von Dreiecken mithilfe der Seitenlängen

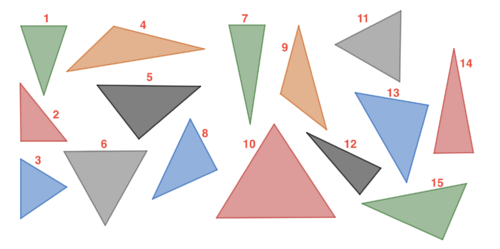
Ordne den Bildern einen richtigen Zettel zu, indem du die verschiedenen Dreiecke zählst. (Hinweis: Klicke auf die Bilder um die Abbildungen größer zu sehen)

zurück zum Arbeitsblatt

Überlege dir mithilfe der Zuordnungen, wann ein Dreieck gleichschenklig oder gleichseitig ist. Notiere deine Überlegungen auf deinem Arbeitsblatt.

Merksatz: Unterscheidung von Dreiecken mithilfe von Seitenlängen

Fülle den folgenden Merksatz aus.

Hat ein Dreieck zwei gleich lange Seiten, nennt man es auch gleichschenkliges Dreieck. Sind alle Seiten gleich lang heißt das Dreieck gleichseitiges Dreieck.

zurück zum Arbeitsblatt

Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt.

Weiterführende Aufgaben

Info

Du hast nun gelernt, wie man Dreiecke mithilfe von Winkeln und Seitenlängen unterscheiden kann. Die folgenden Aufgaben kombinieren nun diese beiden Unterscheidungen. Die folgenden Aufgaben haben unterschiedliche Schwierigkeitsgrade. Du kannst frei entscheiden, welche der Aufgaben du bearbeiten möchtest.

 

Aufgabe 4: Zuordnung von Dreiecksarten

Entscheide, ob es sich bei dem gezeigten Dreieck um ein gleichschenkliges Dreieck, ein gleichseitiges Dreieck, ein rechtwinkliges Dreieck oder ein allgemeines Dreieck handelt.

Wenn du dir unsicher bist, schaue die Bezeichnungen noch einmal im Merksatz nach. (Hinweis: Es können mehrere Antworten richtig sein.)

Aufgabe 4: Eigenschaften von Dreiecken

Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung.

1. Ein rechtwinkliges Dreieck kann gleichschenklig sein.
2. Jedes gleichseitige Dreieck ist immer spitzwinklig.
3. Ein stumpfwinkliges Dreieck kann rechtwinklig sein.

1. Ja, es kann gleichschenklig sein. Es ist ein Dreieck mit zweimal 45° Winkeln und einem rechten Winkel.

2. Ja, das stimmt. In einem gleichseitiges Dreieck sind alle Winkel 60°.

3. Das ist nicht wahr. Versuche mal ein Dreieck zu zeichnen, das einen stumpfen Winkel und einen rechten Winkel hat. Dann fällt dir vielleicht auf, dass das nicht möglich ist.

Kapitel 4 Aufgabe

Aufgabe zu besonderen Dreiecken

Löse das Kreuzworträtsel, indem du die fehlenden Wörter zum Thema Dreiecke findest.