|
|
| Zeile 31: |
Zeile 31: |
| Bewege die verschiedenen Punkte und schaue dir an, wie sich die Winkel und Seiten sich verändern. | | Bewege die verschiedenen Punkte und schaue dir an, wie sich die Winkel und Seiten sich verändern. |
|
| |
|
| <ggb_applet id="zskfsssd" width="1000" height="611" border="888888" />|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} | | <ggb_applet id="gbscAC4x" width="1000" height="611" border="888888" />|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} |
|
| |
|
| {{Box|1= Aufgabe 2: Grundlagen zu Scheitelwinkeln|2= '''1.''' Untersuche das folgende GeoGebra-Applet, indem du dir die Winkel anzeigen lässt und die Position der Geraden veränderst. Verschiebe hierfür die Punkte '''A''' und '''B'''.
| |
|
| |
|
| '''2.''' Beschreibe danach deine Beobachtungen, indem du den unten stehenden Lückentext ausfüllst.
| |
|
| |
|
| <ggb_applet id="XXAVyaqp" width="1000" height="1000" border="888888" />
| |
| (Applet von I. Schwalbe)
| |
|
| |
|
| <div class="lueckentext-quiz">
| |
| Wenn ich die Lage der Geraden zueinander verändere, so verändern sich auch '''die Winkel''' am Schnittpunkt. Außerdem bleiben die Winkel <math>\alpha</math> und <math>\beta</math> '''gleich groß''', genau so wie die Winkel <math>\gamma</math> und <math>\delta</math>. Zwei nebeneinander liegende Winkel addieren sich immer zu '''<math>180^\circ</math>'''. Deshalb ergibt <math>\alpha +\beta +\gamma +\delta=</math> '''<math>360^\circ</math>'''.
| |
| </div>
| |
|
| |
|
|
| |
|
| <br /><br />
| | {{Box|1= Aufgabe 3|2= |
| |3= Arbeitsmethode | Farbe={{Farbe|orange}} }}
| |
| | |
| | |
| | |
| | |
| {{Box|1= Aufgabe 3: Erarbeitung|2= | |
| Wieviele Dreiecke kannst du in den Bildern zählen? Ordne die richtige Antwort dem entsprechenden Bild zu. | | Wieviele Dreiecke kannst du in den Bildern zählen? Ordne die richtige Antwort dem entsprechenden Bild zu. |
| <iframe src="https://learningapps.org/watch?v=pm6g8en6a22" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|3=Merksatz| Farbe={{Farbe|orange}}}} | | <iframe src="https://learningapps.org/watch?v=pm6g8en6a22" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|3=Merksatz| Farbe={{Farbe|orange}}}} |
Version vom 29. April 2022, 12:41 Uhr
Info
In diesem Lernpfadkapitel entdeckst du, wie du Dreiecke vergleichen kannst. Dabei lernst du die verschiedenen Dreiecksarten kennen.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Teste dein Vorwissen
Wiederholungsaufgabe
Erinnerst du dich noch an die verschiedenen Winkelarten? Teste dein Vorwissen mithilfe der folgenden Aufgabe.
{{Box|1=Erinnerung: Winkelarten|
{{{1}}}
Aufgabe 1
In der Abbildung siehst du verschiedenste Dreiecke.
Gib Dreiecke an, die Gemeinsamkeiten haben, und beschreibe diese Gemeinsamkeiten kurz auf dem Arbeitsblatt.
(Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form.)
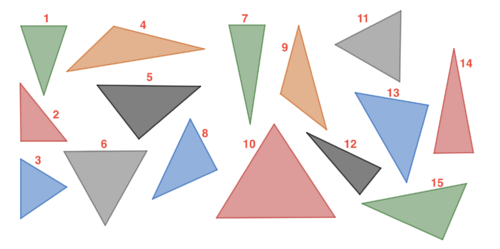
Hier sind verschiedene Arten von Dreiecke dargestellt.
Du kannst Dreiecke vergleichen, indem du ihre Winkel oder ihre Seitenlängen vergleichst.
Merksatz: Winkelgrößen
Aufgabe zur Unterscheidung von Dreiecken mithilfe von Winkeln:
Bewege die verschiedenen Punkte und schaue dir an, wie sich die Winkel und Seiten sich verändern.
Aufgabe 3
Wieviele Dreiecke kannst du in den Bildern zählen? Ordne die richtige Antwort dem entsprechenden Bild zu.
Merksatz
Merksatz: Unterscheidung von Dreiecken
Ein spitzwinkliges Dreieck hat drei spitze Winkel (<90°).
Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel.
Ein rechtwinkliges Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel.
Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel.
In der Abbildung kannst du noch einmal alle verschiedenen Arten von Dreiecken sehen. Miteinander verbundene Dreiecksarten haben immer eine Gemeinsamkeit.
Vertiefung
Aufgabe 4: Vertiefung
Ordne die Dreiecke ihren Bezeichnungen zu. Wenn du dir unsicher bist, schaue die Bezeichnungen noch einmal im Merksatz nach.
Aufgabe 4: Vertiefung
Zeichne die folgenden Dreiecke:
- ein rechtwinkliges Dreieck
- ein gleichschenkliges Dreieck
- ein gleichseitiges Dreieck
- ein stumpfes Dreieck
- ein gleichschenkliges, rechtwinkliges Dreieck
Aufgabe 4: Vertiefung
Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung.
- Ein rechtwinkliges Dreieck kann gleichschenklig sein.
- Jedes gleichseitige Dreieck ist immer spitzwinklig.
- Ein stumpfwinkliges Dreieck kann rechtwinklig sein.
1. Ja, es kann gleichschenklig sein. Es ist ein Dreieck mit zweimal 45° Winkeln und einem rechten Winkel.
2. Ja, das stimmt. In einem gleichseitiges Dreieck sind alle Winkel 60°.
3. Das ist nicht wahr. Versuche mal ein Dreieck zu zeichnen, das einen stumpfen Winkel und einen rechten Winkel hat. Dann fällt dir vielleicht auf, dass das nicht möglich ist.
Kapitel 4 Aufgabe
Noch zu erledigen
- Ideen für die Aufgaben entwickeln
- Merksatz schreiben
- Kapitel 4 Aufgaben suchen/erfinden
- Info-Boxen erstellen (als Wiederholung Klasse 6)






