|
|
| Zeile 41: |
Zeile 41: |
| {{Box|1=Aufgabe 2: Erarbeitung|2=Aufgabe zur Unterscheidung von Dreiecken mithilfe von Winkeln: | | {{Box|1=Aufgabe 2: Erarbeitung|2=Aufgabe zur Unterscheidung von Dreiecken mithilfe von Winkeln: |
|
| |
|
| Bewege den Punkt C von links nach rechts und finde heraus welche drei verschiedene Dreiecke es gibt. Notiere ihren Namen und ihre Besonderheiten dazu. Kontrolliere später mit dem Merksatz, ob du richtig lagst. | | Bewege die verschiedenen Punkte und schaue dir an, wie sich die Winkel und Seiten verändern. |
|
| |
|
| <ggb_applet id="SANyzFbu" width="1000" height="611" border="888888" />|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} | | <ggb_applet id="wqqeqk9b" width="1000" height="611" border="888888" />|3=Arbeitsmethode |Farbe={{Farbe|orange}}}} |
|
| |
|
|
| |
|
Version vom 10. April 2022, 19:32 Uhr
Info
Auf dieser Seite lernst du verschiedene Dreiecksarten kennen.
Fachdidaktische Analyse
Leitfrage
Wie können wir Dreieck vergleichen?
- Symmetrien werden ausgelassen (erhöht Komplexität unnötig) - Fokus: Seitenmessung
- notwendiges Vorwissen: Winkelarten, Winkel- und Seitenmessung - sollte vorhanden sein (evtl. mit Infokästen wiederholt)
- Aufgaben eher mit Geogebra als händisch - Zeitersparnis, Erdkundungsmöglichkeit
- prozeduales Wissen: Dreieckskonstruktionen mit Geogebra
- konzeptuelles Wissen: Dreiecksunterscheidungen (Lernziel)
- anspruchsvollere Aufgaben: Verknüpfung von Dreiecksaufgaben - Transferaufgaben (gleichseitig => nicht rechtwinklig)
- Infoboxen als Wiederholung aus der sechsten Klasse (z.B. spitzer Winkel)
Wiederholungseinheit
Wiederholungsaufgabe
Du hast bereits verschiedene Winkelarten kennengelernt. Teste dein Wissen mithilfe der folgenden Aufgabe.
Merksatz: Winkelarten (Wiederholung)
Man unterscheidet Winkel nach ihrer Größe.
Spitze Winkel sind kleiner als 90°, rechte Winkel sind 90°, stumpfe Winkel sind größer als 90°, aber kleiner als 180°.
Einen Winkel, der größer ist als 180°, nennt man überstumpf.
Erkundungsaufgabe zum Einstieg (Aktivierung)
Aufgabe 1: Aktivierung
In der Abbildung siehst du verschiedenste Dreiecke. Es gibt in der Abbildung Dreiecke, die Gemeinsamkeiten haben.
Gib Dreiecke an, die Gemeinsamkeiten haben, und beschreibe diese Gemeinsamkeiten kurz auf dem Arbeitsblatt.
(Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form.)
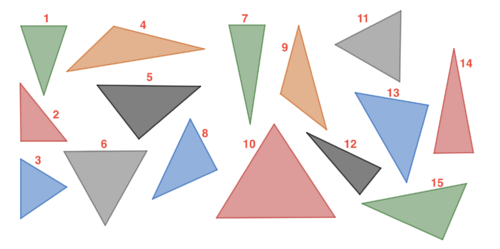
Hier sind verschiedene Arten von Dreiecke dargestellt.
Du kannst Dreiecke vergleichen, indem du ihre Winkel oder ihre Seitenlängen vergleichst.
Erarbeitung
Aufgabe 2: Erarbeitung
Aufgabe zur Unterscheidung von Dreiecken mithilfe von Winkeln:
Bewege die verschiedenen Punkte und schaue dir an, wie sich die Winkel und Seiten verändern.
Aufgabe 3: Erarbeitung
Aufgabe zur Unterscheidung von Dreiecken mithilfe von Seiten.
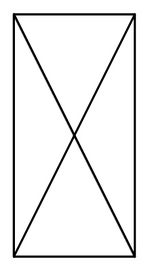
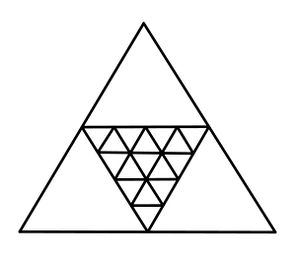
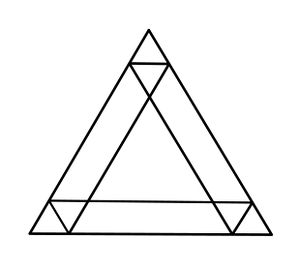
Zähle wie viele gleichschenklige Dreiecke in der Figur enthalten sind. Wie viele davon sind sogar gleichseitig?
To-Do: Lösung zum ausklappen, evtl. Tipp bei 2 und 3
Merksatz
Merksatz: Unterscheidung von Dreiecken
Ein spitzwinkliges Dreieck hat drei spitze Winkel (<90°).
Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel.
Ein rechtwinkliges Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel.
Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel.
In der Abbildung kannst du noch einmal alle verschiedenen Arten von Dreiecken sehen. Miteinander verbundene Dreiecksarten haben immer eine Gemeinsamkeit.
Vertiefung
Aufgabe 4: Vertiefung
Ordne die Dreiecke ihren Bezeichnungen zu. Wenn du dir unsicher bist, schaue die Bezeichnungen noch einmal im Merksatz nach.
Aufgabe 4: Vertiefung
Zeichne die folgenden Dreiecke:
- ein rechtwinkliges Dreieck
- ein gleichschenkliges Dreieck
- ein gleichseitiges Dreieck
- ein stumpfes Dreieck
- ein gleichschenkliges, rechtwinkliges Dreieck
Aufgabe 4: Vertiefung
Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung.
- Ein rechtwinkliges Dreieck kann gleichschenklig sein.
- Jedes gleichseitige Dreieck ist immer spitzwinklig.
- Ein stumpfwinkliges Dreieck kann rechtwinklig sein.
1. Ja, es kann gleichschenklig sein. Es ist ein Dreieck mit zweimal 45° Winkeln und einem rechten Winkel.
2. Ja, das stimmt. In einem gleichseitiges Dreieck sind alle Winkel 60°.
3. Das ist nicht wahr. Versuche mal ein Dreieck zu zeichnen, das einen stumpfen Winkel und einen rechten Winkel hat. Dann fällt dir vielleicht auf, dass das nicht möglich ist.
Kapitel 4 Aufgabe
Noch zu erledigen
- Ideen für die Aufgaben entwickeln
- Merksatz schreiben
- Kapitel 4 Aufgaben suchen/erfinden
- Info-Boxen erstellen (als Wiederholung Klasse 6)