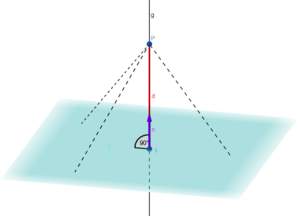
Der Abstand zweier windschiefer Geraden  und
und  ist die kürzeste Verbindung zwischen einem Punkt der Geraden
ist die kürzeste Verbindung zwischen einem Punkt der Geraden  und einem Punkt der Geraden
und einem Punkt der Geraden  . Diese kürzeste Verbindungsstrecke
. Diese kürzeste Verbindungsstrecke  zwischen den beiden Geraden ist sowohl orthogonal zu
zwischen den beiden Geraden ist sowohl orthogonal zu  als auch orthogonal zu
als auch orthogonal zu  und heißt gemeinsames Lot der windschiefen Geraden
und heißt gemeinsames Lot der windschiefen Geraden  und
und  .
.
Für die Bestimmung des Abstandes  berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst:
Seien
berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst:
Seien  und
und  die windschiefen Geraden.
die windschiefen Geraden.
Verfahren Gemeinsames Lot
- Bestimme die Geradenpunkte
 und
und  in Abhängigkeit von dem jeweiligen Geradenparameter.
in Abhängigkeit von dem jeweiligen Geradenparameter.
- Stelle den Verbindungsvektor
 in Abhängigkeit von den Geradenparametern auf.
in Abhängigkeit von den Geradenparametern auf.
- Bestimme nun die Parameter
 und
und  so, dass der Verbindungsvektor
so, dass der Verbindungsvektor  orthogonal zu den Richtungsvektoren von
orthogonal zu den Richtungsvektoren von  und
und  ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen
ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen  und
und  .
.
- Mit diesen Parametern erhältst du die Lotfußpunkte
 und
und  und kannst den Abstand
und kannst den Abstand  bestimmen.
bestimmen.
Verfahren Hilfsebene
Es gibt eine Ebene  , sodass
, sodass  in
in  liegt und
liegt und  parallel zu
parallel zu  ist. Für diese Ebene
ist. Für diese Ebene  ist dann der Abstand zwischen den Geraden
ist dann der Abstand zwischen den Geraden  gleich dem Abstand zwischen
gleich dem Abstand zwischen  und einem beliebigen Punkt
und einem beliebigen Punkt  auf
auf  .
.
1. Stelle die Ebenengleichung in Koordinatenform der Ebene  auf, sodass die GErade
auf, sodass die GErade  in
in  liegt und die Gerade
liegt und die Gerade  parallel zu
parallel zu  ist:
ist:
Jeder Normalenvektor von dieser Ebene  ist orthogonal zu den Richtungsvektoren von den Geraden
ist orthogonal zu den Richtungsvektoren von den Geraden  und
und  . Bestimme also aus den Gleichungen
. Bestimme also aus den Gleichungen  und
und  einen Normalenvektor
einen Normalenvektor  .
Die Ebenengleichung in Koordinatenform ist dann
.
Die Ebenengleichung in Koordinatenform ist dann  .
.
Die Gerade  soll in
soll in  liegen. Bestimme also
liegen. Bestimme also  , indem du einen Punkt der Geraden
, indem du einen Punkt der Geraden  in die Ebenengleichung einsetzt.
in die Ebenengleichung einsetzt.
2. Wähle einen beliebigen Punkt  auf der Geraden
auf der Geraden  . (Da
. (Da  parallel zu
parallel zu  ist, haben alle Punkte von
ist, haben alle Punkte von  den gleichen Abstand zu
den gleichen Abstand zu  .)
.)
3. Bestimme mit der Formel für den Abstand eines Punktes von einer Ebene oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand  . So, wie wir die Ebene
. So, wie wir die Ebene  konstruiert haben, ist nun der Abstand zwischen den windeschiefen Geraden
konstruiert haben, ist nun der Abstand zwischen den windeschiefen Geraden  .
.
Beispiel:
Wir bestimmen den Abstand der windschiefen Geraden  und
und  .
.
Mit dem Verfahren Gemeinsames Lot:
1. Geradenpunkte  und
und  in Abhängigkeit von dem jeweiligen Geradenparameter:
in Abhängigkeit von dem jeweiligen Geradenparameter:
 und
und 
2. Verbindungsvektor  in Abhängigkeit von den Geradenparametern
in Abhängigkeit von den Geradenparametern  und
und  :
:

3.  und
und  so bestimmen, dass
so bestimmen, dass  orthogonal zu den Richtungsvektoren von
orthogonal zu den Richtungsvektoren von  und
und  ist, also das lineare Gelichungssystem
ist, also das lineare Gelichungssystem  und
und  lösen:
lösen:
 und
und  liefert
liefert  und
und  .
.
4. Damit erhält man die Lotfußpunkte  und
und  .
Also ist
.
Also ist  .
.
Mit dem Verfahren Hilfsebene:
1. Ebenengleichung der Ebene  , sodass
, sodass  in
in  liegt und
liegt und  parallel zu
parallel zu  ist, aufstellen:
ist, aufstellen:
Der Normalenvektor ist orthogonal zu den Richtungsvektoren von  und
und  , also gilt:
, also gilt:
 und
und 
bzw.  und Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 0=4n_1-5_n_2+2n_3}
.
und Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 0=4n_1-5_n_2+2n_3}
.
Dieses Gleichungssystem ergibt  als möglichen Normalenvektor.
als möglichen Normalenvektor.
Also ist  .
.
Einen Punkt der Geraden  einsetzen, um
einsetzen, um  zu erhalten (denn die Gerade
zu erhalten (denn die Gerade  soll in der Ebene
soll in der Ebene  liegen):
liegen):
Wir nehmen den Punkt  auf
auf  . Also ist
. Also ist  und insgesamt
und insgesamt  .
.
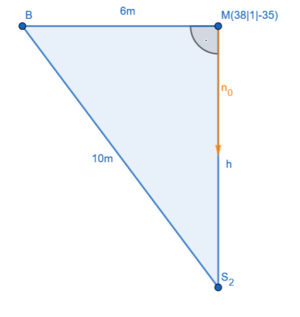
2. Einen beliebigen Punkt  auf der Geraden
auf der Geraden  wählen: Wir nehmen
wählen: Wir nehmen  .
.
3. Abstand mit der Formel zur Berechnung des Abstandes zwischen einem Punkt und einer Ebene bestimmen:
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle d(g;h)=d(E;H)=\frac {|-\frac{7}{4}\cdot 7 + (-1)\cdot 7 + 1\cdot 0-1|}{\sqrt{(-\frac{7}{4)^2+(-1)^2+1^2}}=9}