Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 318: | Zeile 318: | ||
{{Box | {{Box | ||
|Aufgabe 6: Spurpunkte einer Geraden | |Aufgabe 6: Spurpunkte einer Geraden (Besonderheiten) | ||
|Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du | |Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du den Aufpunktvektor <math>vec{a}</math> und den Richtungsvektor <math>vec{u}</math> mit den Schiebereglern entsprechend anpassen. Anschließend kannst du dir die drei Spurpunkte und ggf. auch die Ebenen anzeigen lassen, indem du das entsprechende Feld ankreuzt. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen: | ||
<ggb_applet id=" | <ggb_applet id="ynkzgreu" width="100%" height="100%" /> | ||
{{ | Untersuche die Geraden, die aus folgenden Aufpunkt- und Richtungsvektoren hervorgehen, auf Spurpunkte und schreibe die Spurpunkte auf. Was sagt die Lage der Geraden über die Anzahl der Spurpunkte aus? | ||
'''a)''' <math>vec{a} = \begin{pmatrix} 3 \\ 1 \\ -1 \end{pmatrix}, vec{u} = \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}</math> | |||
'''b)''' <math>vec{a} = \begin{pmatrix} 1,5 \\ 3 \\ -2 \end{pmatrix}, vec{u} = \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}</math> | |||
'''c)''' <math>vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, vec{u} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}</math> | |||
'''d)''' <math>vec{a} = \begin{pmatrix} 5 \\ 0 \\ 1 \end{pmatrix}, vec{u} = \begin{pmatrix} 3 \\ 0 \\ 1,5 \end{pmatrix}</math> | |||
{{Lösung versteckt | |||
|Betrachte mal ggf. vorhandene Parallelitäten der Geraden zu den Koordinatenebenen. Fällt dir nun etwas auf? | |||
|Tipp für alle Aufgaben anzeigen | |||
|Tipp für alle Aufgaben verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Die drei Spurpunkte lauten <math>S_{12}(4,5|0,5|0)</math>, <math>S_{13}(6|0|1)</math> und <math>S_{23}(0|2|{-}3)</math>. Da die Gerade nicht parallel zu den Koordinatenebenen verläuft, besitzt sie drei Spurpunkte. | |||
|Lösung Aufgabe a) anzeigen | |||
|Lösung Aufgabe a) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Die zwei Spurpunkte lauten <math>S_{12}(4,5|3|0)</math> und <math>S_{23}(0|3|{-}3)</math>. Da die Gerade parallel zur <math>x_1x_3</math>-Ebene verläuft, hat sie keinen Schnittpunkt mit dieser und besitzt folglich nur zwei Spurpunkte. | |||
|Lösung Aufgabe b) anzeigen | |||
|Lösung Aufgabe b) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Der einzige Spurpunkt lautet <math>S_{23}(0|2|3)</math>. Da die Gerade sowohl parallel zur <math>x_1x_2</math>-Ebene als auch parallel zur <math>x_1x_3</math>-Ebene verläuft, hat sie keine Schnittpunkte mit diesen und besitzt folglich nur einen Spurpunkt. | |||
|Lösung Aufgabe c) anzeigen | |||
|Lösung Aufgabe c) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Die zwei Spurpunkte lauten <math>S_{12}(3|0|0)</math> und <math>S_{23}(0|0|{-}1,5)</math>. Da die Gerade innerhalb der <math>x_1x_3</math>-Ebene verläuft, hat sie unendlich viele Schnittpunkte mit dieser. | |||
|Lösung Aufgabe c) anzeigen | |||
|Lösung Aufgabe c) verbergen | |||
}} | |||
|Arbeitsmethode | |Arbeitsmethode | ||
|Farbe={{Farbe|orange}} | |Farbe={{Farbe|orange}} | ||
}} | }} | ||
{{Box | {{Box | ||
|Aufgabe 7: Spurpunkte einer Geraden | |Aufgabe 7: Spurpunkte einer Geraden | ||
|Berechne die Spurpunkte der Geraden <math>g</math>. | |Berechne die Spurpunkte der Geraden <math>g</math>. | ||
Version vom 1. Juni 2021, 11:21 Uhr
Geraden und ihre Darstellungsformen
Parameterdarstellung einer Geraden
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, kannst du hier noch einmal nachvollziehen.
Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.
Punktprobe
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du hier noch einmal nachschauen.
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:
Spurpunkte einer Geraden
Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du hier noch einmal nachvollziehen.
Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen:
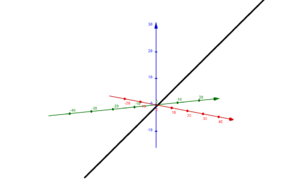
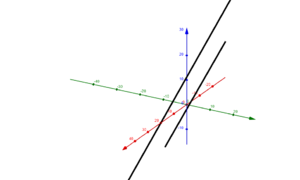
Die -Ebene ist die Ebene, die von der - und -Achse aufgespannt wird (im Bild genannt). Entsprechendes gilt für die - (im Bild ) und -Ebene (im Bild ).
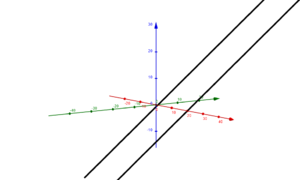
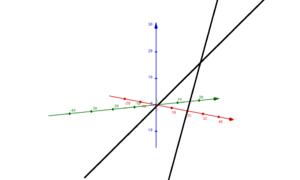
Lagebeziehungen von Geraden
Parallele und identische Geraden