Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum

Info

In diesem Lernpfadkapitel beschäftigst du dich mit Geraden im Raum. Du lernst, Geraden im Raum durch Vektoren zu beschreiben, Parameterdarstellungen und Spurpunkte von Geraden zu bestimmen, die Lage von Geraden im Raum und zueinander zu bestimmen sowie Geradenscharen zu bestimmen.

Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit und
• Aufgaben mit grünem Streifen sind Knobelaufgaben.

Wir wünschen dir viel Erfolg!

Geraden und ihre Darstellungsformen

Parameterdarstellung einer Geraden

Definition

Jede Gerade lässt sich durch eine Gleichung der Form $g \colon \vec{x} = \vec{OA} + k \cdot \vec{v}$ mit $k \in \mathbb{R}$ beschreiben.

• Diese Vektorgleichung bezeichnet man als Parameterdarstellung oder Parametergleichung der Geraden $g$ mit dem Parameter $k$.
• Setzt man für $k$ irgendeine Zahl in die Parameterdarstellung der Geraden $g$ ein, so ergibt sich der Ortsvektor $\vec{x}$ (auch $\vec{OX}$ genannt) eines Punktes $X$ der Geraden $g$.
• Der Vektor $\vec{OA}$ heißt Stützvektor. Er ist der Ortsvektor zu einem Punkt $A$ (auch Aufpunkt genannt), der auf der Geraden $g$ liegt.
• Der Vektor $\vec{v} \neq \vec{o}$ heißt Richtungsvekor.

Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, kannst du hier noch einmal nachvollziehen.

Aufgabe 1: Geradengleichung aufstellen (zwei gegebene Punkte)

Im Folgenden kannst du sehen, wie die Gerade vom Stützpunkt $A$, Richtungsvektor $\vec{v}$ und Parameter $t$ abhängt. Wähle verschiedene Stützpunkte und Richtungsvektoren und verändere den Parameter. Wo liegt der Punkt $P$, wenn du $t < 0$, $t = 0$ und $t > 0$ wählst? Was bedeutet dies anschaulich? Dazu kannst du dir auch die Gerade $g$ anzeigen lassen.

• Für $t < 0$ liegt der Punkt $P$ hinter dem Punkt $A$, d.h. man geht auf der Gerade vom Stützpunkt aus gesehen rückwärts.
• Für $t = 0$ liegt der Punkt $P$ genau auf dem Punkt $A$, d.h. sie sind identisch, man befindet sich also genau auf dem Stützpunkt.
• Für $t > 0$ liegt der Punkt $P$ vor dem Punkt $A$, d.h. man geht auf der Gerade vom Stützpunkt aus gesehen vorwärts.

Bearbeite nun entweder die analoge Aufgabe (I) oder die digitale Aufgabe (II):

(I) Die Gerade $g$ geht durch die Punkte $A$ und $B$. Gib zwei Gleichungen für $g$ an.

a) $A(1|2|2), B(5|{-}4|7)$

b) $A(-3|{-}2|9), B(0|0|3)$

Wie du im obigen Video gesehen hast, gibt es unendlich viele Lösungen, denn es sind immer Vielfache des Richtungsvektors möglich. Daher ist es möglich, dass deine Lösung hier zwar nicht aufgefürt, aber dennoch korrekt ist. Dazu überprüfe, ob dein Richtungsvektor ein Vielfaches einer der angegeben Richtungsvektoren ist. Beachte das auch bei allen folgenden Aufgaben!

Zwei mögliche Geraden sind $g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -6 \\ 5 \end{pmatrix}, s \in \mathbb{R}$ und $g \colon \vec{x} = \begin{pmatrix} 5 \\ -4 \\ 7 \end{pmatrix} + t \cdot \begin{pmatrix} -4 \\ 6 \\ -5 \end{pmatrix}, t \in \mathbb{R}$.

Zwei mögliche Geraden sind $g \colon \vec{x} = \begin{pmatrix} -3 \\ -2 \\ 9 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}, s \in \mathbb{R}$ und $g \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \\ 6 \end{pmatrix}, t \in \mathbb{R}$.

(II) Ordne jeweils die zwei Punkte A und B der Parametergleichung der Geraden durch A und B zu.

Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt $P$ verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.

Aufgabe 2: Geradengleichung aufstellen auf Punkt und Richtungsvektor

Stelle jeweils eine Geradengleichung auf.

a) Die Gerade $g$ geht durch den Punkt $P(1|{-}1|2)$ und hat den Richtungsvektor $\vec{v} = \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}$.

Überlege dir wie der Stützvektor der Geraden lauten muss und stelle dann die passende Geradengleichung mit dem Richtungsvektor auf.

b) Stelle eine Geradengleichung für die $x_1$-Achse auf.

Überlege dir einen geschickten Aufpunkt; wie muss dann der Richtungsvektor aussehen?

c) Die Gerade $g$ geht durch den Punkt $P(2|{-}2|4)$ und verläuft parallel zur Geraden $h: \vec{x} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, r \in \mathbb{R}$.

Wann verlaufen zwei Vektoren parallel zueinander? Übertrage diese Kenntniss auf Geraden.

d) Die Gerade $g$ geht durch den Punkt $P(1|{-}1|{-}2)$ und verläuft parallel zur $x_1$-Achse.

e) Die Gerade $g$ geht durch den einen beliebigen Punkt $P(p_1|p_2|p_3)$ und verläuft parallel zur $x_3$-Achse.

Diese Aufgabe funktioniert ähnlich zu d).

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}, s \in \mathbb{R}$.

Eine mögliche Gerade ist $x_1 \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R}$ oder noch einfacher $x_1 \colon \vec{x} = s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R}$

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, s \in \mathbb{R}$.

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R}$.

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, s \in \mathbb{R}$.

Punktprobe

Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du hier noch einmal nachschauen.

Merksatz: Punktprobe

Liegt ein Punkt $P$ auf der Geraden g definiert durch $g: \vec{x} = \vec{a} + k \cdot \vec{v}$ mit $k \in \mathbb{R}$, so gibt es genau ein $k$, welches die Gleichung $\vec{p} = \vec{a} + k \cdot \vec{v}, r \in \mathbb{R}$ erfüllt. Erfüllt kein $k$ diese Gleichung, liegt der Punkt nicht auf der Geraden.

Aufgabe 3: Punktprobe mit einer Geraden I

Überprüfe, ob der Punkt $P$ auf der Geraden $g$ liegt.

a) $P(2|3|{-}1), g \colon \vec{x} = \begin{pmatrix} 7 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 5 \\ -3 \\ 5 \end{pmatrix}, r \in \mathbb{R}$

b) $P(2|{-}1|{-}1), g \colon \vec{x} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 3 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die Punktprobe ist erfüllt, denn:

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \begin{pmatrix} 2 \\ 3 \\ -1 \end{pmatrix} = \begin{pmatrix} 7 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 5 \\ -3 \\ 5 \end{pmatrix} \Leftrightarrow\left\vert\begin{alignat}{7} 2 &&\; = \;&& 7 &&\; + \;&& 5r \\ 3 &&\; = \;&& 0 &&\; - \;&& 3r \\ -1 &&\; = \;&& 4 &&\; + \;&& 5r \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& -1 \\ r &&\; = \;&& -1 \\ r &&\; = \;&& -1 \end{alignat}\right\vert}

Somit liegt der Punkt $P$ auf der Geraden $g$.

Die Punktprobe ist nicht erfüllt, denn:

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \begin{pmatrix} 2 \\ -1 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 3 \\ 3 \end{pmatrix} \Leftrightarrow\left\vert\begin{alignat}{7} 2 &&\; = \;&& 1 &&\; + \;&& r \\ -1 &&\; = \;&& 0 &&\; + \;&& 3r \\ -1 &&\; = \;&& 1 &&\; + \;&& 3r \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& 1 \\ r &&\; = \;&& -\frac{1}{3} \\ r &&\; = \;&& -\frac{2}{3} \end{alignat}\right\vert}

Es ergibt sich ein Widerspruch. Somit liegt der Punkt $P$ nicht auf der Geraden $g$.

Aufgabe 4: Punktprobe mit einer Geraden II

Für welche Werte $s, r \in \mathbb{R}$ liegt der Punkt $P$ auf der Geraden $g: \vec{x} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}$?

a) $P(13|3|0)$

b) $P(5|{-}2|0)$

Berechne zunächst mithilfe der ersten Gleichung einen Wert für $r$. Was könnte man nun machen?

Setze nun den ausgerechneten Wert für $r$ in die beiden anderen Gleichungen ein und berechne $s$.

Die Punktprobe ist erfüllt, denn:

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \begin{pmatrix} 13 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \Leftrightarrow\left\vert\begin{alignat}{7} 13 &&\; = \;&& 9 &&\; + \;&& 2r \\ 3 &&\; = \;&& -s &&\; + \;&& r \\ 0 &&\; = \;&& 2s &&\; + \;&& r \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& 2 \\ 3 &&\; = \;&& -s &&\; + \;&& 2 \\ 0 &&\; = \;&& 2s &&\; + \;&& 2 \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& 2 \\ s &&\; = \;&& -1 \\ s &&\; = \;&& -1 \end{alignat}\right\vert}

Somit liegt der Punkt $P$ für $r = 2$ und $s = -1$ auf der Geraden $g$.

Es gibt keine Lösung, denn:

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \begin{pmatrix} 5 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \Leftrightarrow\left\vert\begin{alignat}{7} 5 &&\; = \;&& 9 &&\; + \;&& 2r \\ -2 &&\; = \;&& -s &&\; + \;&& r \\ 0 &&\; = \;&& 2s &&\; + \;&& r \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& -2 \\ -2 &&\; = \;&& -s &&\; + \;&& -2 \\ 0 &&\; = \;&& 2s &&\; + \;&& -2 \end{alignat}\right\vert \Leftrightarrow\left\vert\begin{alignat}{7} r &&\; = \;&& 2 \\ s &&\; = \;&& 0 \\ s &&\; = \;&& 1 \end{alignat}\right\vert}

Es ergibt sich ein Widerspruch, weshalb keine Werte für Punkt $s, r$ gibt, sodass der Punkt $P$ auf der Geraden $g$ liegt.

Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:

Aufgabe 5: Besondere Geraden im Raum

Kreuze alle(!) richtigen Antworten an!

Spurpunkte einer Geraden

Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du hier noch einmal nachvollziehen.

Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen:

Die $x_1x_2$-Ebene ist die Ebene, die von der $x_1$- und $x_2$-Achse aufgespannt wird (im Bild $E_{12}$ genannt). Entsprechendes gilt für die $x_1x_3$- (im Bild $E_{13}$) und $x_2x_3$-Ebene (im Bild $E_{23}$).

Aufgabe 6: Besondere Geraden im Raum

Kreuze alle(!) richtigen Antworten an!

Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du die Punkte $A$ und $B$ anpassen, durch die die Gerade verlaufen soll. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen:

Aufgabe 7: Spurpunkte einer Geraden

Berechne die Spurpunkte der Geraden $g$.

a) $g \colon \vec{x} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, r \in \mathbb{R}$

b) $g \colon \vec{x} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}, r \in \mathbb{R}$

c) $g \colon \vec{x} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix}, r \in \mathbb{R}$

1. Für den Schnittpunkt $S_{12}$ der Geraden $g$ mit der $x_1x_2$-Ebene setze die $x_3$-Koordinate $= 0$ und forme nach $r$ um: $0 = 7 + r \cdot 1 \Leftrightarrow r = -7$. Setze nun $r = -7$ in der Geradengleichung ein, um den Schnittpunkt $S_{12}$ zu erhalten: $\vec{S_{12}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + (-7) \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ -7 \\ 0 \end{pmatrix}$.
2. Für den Schnittpunkt $S_{13}$ der Geraden $g$ mit der $x_1x_3$-Ebene setze die $x_2$-Koordinate $= 0$ und forme nach $r$ um: $0 = r$. Setze nun $r = 0$ in der Geradengleichung ein, um den Schnittpunkt $S_{13}$ zu erhalten: $\vec{S_{13}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + 0 \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix}$
3. Für den Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene setze die $x_1$-Koordinate $= 0$ und forme nach $r$ um: $0 = 7 + r \cdot 1 \Leftrightarrow r = -7$. Setze nun $r = -7$ in der Geradengleichung ein, um den Schnittpunkt $S_{12}$ zu erhalten: $\vec{S_{12}} = \begin{pmatrix} 7 \\ 0 \\ 7 \end{pmatrix} + (-7) \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ -7 \\ 0 \end{pmatrix}$. Hinweis (war nicht in der Aufgabe gefordert): Man erkennt, dass es sich um den selben Schnittpunkt handelt wie der Schnittpunkt der Gerade mit der $x_1x_2$-Ebene, also: $S_{12} = S_{23}$.

1. Für den Schnittpunkt $S_{12}$ der Geraden $g$ mit der $x_1x_2$-Ebene setze die $x_3$-Koordinate $= 0$ und forme nach $r$ um: $0 = 2 + r \cdot 1 \Leftrightarrow r = -2$. Setze nun $r = -2$ in der Geradengleichung ein, um den Schnittpunkt $S_{12}$ zu erhalten: $\vec{S_{12}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -8 \\ 0 \end{pmatrix}$.
2. Für den Schnittpunkt $S_{13}$ der Geraden $g$ mit der $x_1x_3$-Ebene setze die $x_2$-Koordinate $= 0$ und forme nach $r$ um: $0 = -4 + r \cdot 2 \Leftrightarrow r = 2$. Setze nun $r = 2$ in der Geradengleichung ein, um den Schnittpunkt $S_{13}$ zu erhalten: $\vec{S_{13}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix}$
3. Für den Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene setze die $x_1$-Koordinate $= 0$ und forme nach $r$ um: $0 = 1 + r \cdot 0 \Leftrightarrow 0 = 1$. Es ergibt sich ein Widerspruch, weshalb es keinen Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene gibt. Somit verläuft $g$ parallel zur $x_2x_3$-Ebene.

1. Für den Schnittpunkt $S_{12}$ der Geraden $g$ mit der $x_1x_2$-Ebene setze die $x_3$-Koordinate $= 0$ und forme nach $r$ um: $0 = 4 + r \cdot (-4) \Leftrightarrow r = 1$. Setze nun $r = 1$ in der Geradengleichung ein, um den Schnittpunkt $S_{12}$ zu erhalten: $\vec{S_{12}} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + 1 \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix}$.
2. Für den Schnittpunkt $S_{13}$ der Geraden $g$ mit der $x_1x_3$-Ebene setze die $x_2$-Koordinate $= 0$ und forme nach $r$ um: $0 = 0 + r \cdot 0 \Leftrightarrow 0 = 0$. Man erhält keine Lösung für den Parameter $r$, aber auch keinen Widerspruch. Somit hat die Gerade unendlich viele Spurpunkte mit er $x_1x_2$-Ebene, da sie innerhalb dieser Ebene verläuft.
3. Für den Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene setze die $x_3$-Koordinate $= 0$ und forme nach $r$ um: $0 = 1 + r \cdot 2 \Leftrightarrow r = -\frac{1}{2}$. Setze nun $r = -\frac{1}{2}$ in der Geradengleichung ein, um den Schnittpunkt $S_{23}$ zu erhalten: $\vec{S_{23}} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} + (-\frac{1}{2}) \cdot \begin{pmatrix} 2 \\ 0 \\ -4 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 6 \end{pmatrix}$.

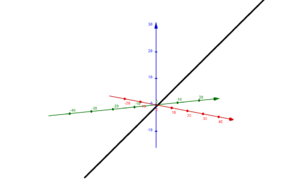
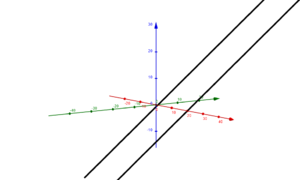
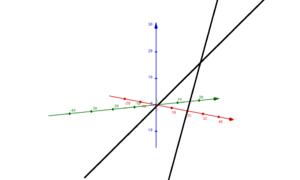
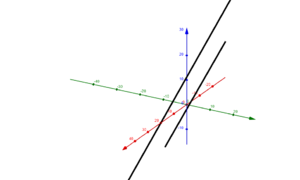
Lagebeziehungen von Geraden

Parallele und identische Geraden

Infobox zur Lagebeziehung zweier Geraden Teil 1

Wir unterscheiden die Lage zweier Geraden in identisch, parallel, sich schneidend und windschief zueinander.

Zwei identische Geraden

Zwei parallele Geraden

Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander kollinear (sind Vielfache voneinander), so können die Geraden lediglich identisch oder parallel sein.

Um nun zu untersuchen, ob die Geraden parallel oder identisch sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden identisch. Andernfalls sind die Geraden parallel zueinander.

Zwei Geraden schneiden sich

Zwei windschiefe Geraden

Sind die Richtungsvektoren nicht kollinear, so können die Geraden sich lediglich schneiden oder windschief zueinander verlaufen. Unter sich schneidene Geraden verstehen wir Geraden, die sich in einem Punkt schneiden. Windschiefe Geraden hingegen sind Geraden, die sich wie die parallelen Geraden zwar nicht schneiden, ihre Richtungsvektoren sind jedoch nicht kollinear.

Um nun zu untersuchen, ob sich die Geraden schneiden oder zueinader winschief zueinander sind, müssen wir schauen, ob sich ein Schnittpunkt berechnen lässt. Hierzu setzen wir die Geradengleichungen gleich und formen um. Erhalten wir einen Schnittpunkt, so schneiden sich die Geraden im Punkt. Andernfalls sind diese Geraden windschief zueinander.

Aufgabe 8: Lage erkennen

Löse das Quiz und mache dir deinen eigenen Lernzettel.

Aufgabe 9: Lage zweier Geraden

Löse den Lückentext und mache dir deinen eigenen Lernzettel.

Aufgabe 10: Lage erkennen

Betrachte die folgenden Geraden $g$ und $h$. Wie verlaufen die Geraden zueinander. Entscheide ohne Nutzung des GTR.

a) $g \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, r \in \mathbb{R}$

b) $g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h \colon \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

c) $g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 4 \\ 4 \end{pmatrix}, r \in \mathbb{R}$ und $h \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} 4 \\ 5 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Hier brauchst du kaum rechnen. Schaue dir die Aufpunkte nochmal genau an.

d) $g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h \colon \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

e) $g \colon \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h \colon \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die erste Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren mit $2\cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}$ ein Vielfaches voneinander (=kollinear) sind. Da beide Stützvektoren identisch sind, weißt du, dass der Punkt $(2|2|5)$ auf beiden Geraden liegt und somit die beiden Geraden identisch sind.

Die zweite Antwort lautet parallel. Die beiden Geraden sind parallel. Während die beiden Richtungsvektoren kollinear, sogar identisch, sind liegt der Aufpunkt $(2|2|2)$ von der Gerade $h$ nicht auf der Geraden von $h \colon \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$, mit

$\left\vert\begin{alignat}{7} 2 &&\; = \;&& 1 &&\; +\;&& r\cdot1\\ 2 &&\; =\;&& 1 &&\; +\;&& r\cdot2\\ 2 &&\; =\;&& 1 &&\; +\;&& r\cdot3 \end{alignat}\right\vert$

Formen wir dies um zu r erhalten wir

$\left\vert\begin{alignat}{7} 1 &&\; = \;&& r\cdot1\\ 1 &&\; =\;&& r\cdot2\\ 1 &&\; =\;&& r\cdot3 \end{alignat}\right\vert$

Formen wir weiter zu $r$ um, erhalten wir

$r=\begin{pmatrix} 1 \\ 0.5 \\ 0.333 \end{pmatrix}$ und damit liegt der Punkt nicht auf der Geraden.

Die dritte Antwort lautet schneiden. Die Richtungsvektoren sind nicht kollinear und damit schneiden sich die beiden Geraden sich im Aufpunkt $(1|2|3)$ selbst.

Die vierte Antwort lautet windschief. Die beiden Geraden sind windschief zueinander. Dies kannst du wie folgt berechnen.

$\left\vert\begin{alignat}{7} 1 &&\; +\;&& r\cdot1 &&\; =\;&& 2 &&\; +\;&& t\cdot1\\ 1 &&\; +\;&& r\cdot2 &&\; =\;&& 3 &&\; +\;&& t\cdot4\\ 1 &&\; +\;&& r\cdot3 &&\; =\;&& 4 &&\; +\;&& t\cdot3 \end{alignat}\right\vert$

Dies formen wir um: $\left\vert\begin{alignat}{7} r\cdot1 &&\; -\;&& t\cdot1 &&\; = \;&& 1 \\ r\cdot2 &&\; -\;&& t\cdot4 &&\; = \;&& 2 \\ r\cdot3 &&\; -\;&& t\cdot3 &&\; = \;&& 3 \end{alignat}\right\vert$

Wenn die erste Zeile mit $2$ multipliziert wird

$\left\vert\begin{alignat}{7} r\cdot2 &&\; -\;&& t\cdot2 &&\; = \;&& 2 \\ r\cdot2 &&\; -\;&& t\cdot4 &&\; = \;&& 2 \\ r\cdot3 &&\; -\;&& t\cdot3 &&\; = \;&& 3 \end{alignat}\right\vert$

und dann von der ersten Zeile die zweite Zeile subtrahiert wird,

$\left\vert\begin{alignat}{7} t\cdot2 &&\; =\;&& 2 \\ r\cdot2 &&\; -\;&& t\cdot4 &&\; =\;&& 2 \\ r\cdot3 &&\; -\;&& t\cdot3 &&\; =\;&& 3 \end{alignat}\right\vert$

erhälst du $t=1$. Wenn du dies in die zweite Zeile einsetzt, erhälst du für $r=3$. Setzt du dies in die letzte Zeile ein, erhälst du $6=3$, eine falsche Aussage. Damit sind die beiden Geraden windschief zueinander.

Die fünfte Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren identisch sind ($\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$) und der Aufpunkt $(2|3|4)$ der Geraden h auf der Geraden g liegt: $\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$.

Aufgabe 11: Flugerlaubnis erteilen?

Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen zwei Flugzeuge starten. Hierzu gehört das Flugzeug der Fluglinie Aer. Es befindet sich bei $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}$ und fliegt innerhalb von 5 Sekunden zum Punkt $\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix}$. Ebenfalls ist das Flugzeug der Fluglinie Amadeus in die Luft. Dies befindet sich in $\begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix}$. Pro Sekunde legt es eine Strecke von $175{,}49$ m zurück und besitzt einen Richtungsvektor von $\begin{pmatrix} 120{,}2 \\ 96{,}4 \\ z \end{pmatrix}$.

Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher. Nutze deinen GTR und hilf ihm die Antworten auf folgende Fragen zu finden:

a) Wie lauten die Geradengleichungen der einzelen Flugzeuge?

Zu Aer: Setze alle gegebenen Daten in eine allgemeine Parameterdarstellung ein und forme um.

Zu Amadeus: Um den Richtungsvektor zu berechnen, benötigst du die Formel zur Berechnung der Länge eines Vektoren:

$L=\sqrt[]{x^{2}+y^{2}+z^{2}}$.

b) Wie schnell (in $\tfrac{km}{h}$) fliegen die einzelnen Flugzeuge?

Geschwindigkeit kann in verschiedene Einheiten angegeben werden, z.B.: $\tfrac{km}{h}$, $\tfrac{m}{s}$ etc.. Nachdem du die Länge der Strecke nach einer Sekunde berechnet hast, musst du dies von $\tfrac{m}{s}$ zu $\tfrac{km}{h}$ umwandeln.

Die Batterien deines GTRs haben den Geist aufgegeben. Es ist immer noch kein Strom vorhanden und der Fluglotse stellt dir die alles entscheidene Frage:

c) Können alle Flugzeuge weiterfliegen, ohne dass es zu einer Kollision kommt?

Nur weil sich zwei Geraden schneiden heißt es noch nicht direkt, dass eine Kollision vorherrscht.

Flugzeug Aer: $f_3\colon \vec{x} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}, t \in \mathbb{R}$ Wobei $t$ für die Zeit in Sekunden steht.

Dies erhälst du, indem du folgendes berechnest: $\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 5\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}, t \in \mathbb{R}$. Dies musst du in ein Gleichugssystem umformen und dies dann zu $x$,$y$ und $z$ auflösen:

$\left\vert\begin{alignat}{7} 510 &&\; =\;&& 10 &&\; +\;&& 5\cdot x\\ 410 &&\; =\;&& 10 &&\; +\;&& 5\cdot y\\ 350 &&\; =\;&& 0 &&\; +\;&& 5\cdot z \end{alignat}\right\vert$

Zunächst bringst du die Zahlen auf die andere Seite: $\left\vert\begin{alignat}{7} 500 &&\; =\;&& 5\cdot x\\ 400 &&\; =\;&& 5\cdot y\\ 350 &&\; =\;&& 5\cdot z \end{alignat}\right\vert$

und formst dann zu $x$,$y$, und $z$ um: $\left\vert\begin{alignat}{7} 100 &&\; =\;&& x\\ 80 &&\; =\;&& y\\ 70 &&\; =\;&& z \end{alignat}\right\vert$

Und erhälst damit direkt den Richtungsvektor.

Flugzeug Amadeus: $f_1\colon \vec{x} = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}, t \in \mathbb{R}$ Wobei $t$ für die Zeit in Sekunden steht.

Dies erhälst du wie folgt: Du kennst den Richtungsvektor: $\begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}$. Nun musst du $z$ berechnen. Im Text steht, dass das Flugzeug pro Sekunde eine Strecke von $175{,}49$ m fliegt. Das bedeutet, dass der Richtungsvektor eine Länge von $175{,}49$ besitzt. Dies kannst du mit der Formel der Länge eines Vektor berechnen:

$175{,}49=\sqrt[]{120{,}2^{2}+96{,}4^{2}+z^{2}}$

Indem du beide Seiten zum quadart nimmst, entfällt die Wurzel und es folgt:

$175{,}49^{2}=120{,}2^{2}+96{,}4^{2}+z^{2}$

Du formst zu $z^{2}$ um und ziehst dann die Wurzel. Du erhälst gerundet $84$.

Du berechnest die Geschwindigkeit, indem du die Länge des Richtungsvektors berechnest. Dies erfolgt mit der Formel:$L=\sqrt[]{x^{2}+y^{2}+z^{2}}$.

Fugzeug Aer:

$L=\sqrt[]{100^{2}+80^{2}+70^{2}}$.

$L=145{,}95$.

Du erhälst also eine Geschwindigkeit von $145{,}95$ $\tfrac{m}{s}$. Es gilt: $3{,}6$ $\tfrac{km}{h}$=1 $\tfrac{m}{s}$. Umgerechnet in $\tfrac{km}{h}$ sind das also:

$145{,}95 \cdot3{,}6= 525{,}42$

also eine Geschwindigkeit von $525{,}42$ $\tfrac{km}{h}$.

Flugzeug Amadeus: Das Flugzeug Amadeus legt in einer Sekunde eine Strecke von $175{,}49$ m zurück. Damit hat es eine Geschwindigkeit von $175{,}49$ $\tfrac{m}{s}$. Umgerechnet in $\tfrac{km}{h}$ sind das also:

$175{,}49\cdot3{,}6= 631{,}76$

also eine Geschwindigkeit von $631{,}76$ $\tfrac{km}{h}$.

Flugzeug Aer und Amadeus: Sie schneiden sich für $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 30 \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}= \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + 25 \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}$. Dies erhälst du, wenn du mit dem GTR die beiden Geraden geleichsetzt. Alternativ wollen wir dir hier noch einmal Lösung ohne GTR zeigen. Du erhälst die Lösung, indem dubeide Funktionen gleichsetzen und in ein Gleichungssystem umformen:

$\left\vert\begin{alignat}{7} 10 &&\; +\;&& t\cdot100 &&\; =\;&& 5 &&\; +\;&& s\cdot120{,}2\\ 10 &&\; +\;&& t\cdot80 &&\; =\;&& 0 &&\; +\;&& s\cdot96{,}4\\ 0 &&\; +\;&& t\cdot70 &&\; =\;&& 0 &&\; +\;&& s\cdot84 \end{alignat}\right\vert$

Dann formst du dieses so um, dass alle Zahlen auf einer Seite sind:

$\left\vert\begin{alignat}{7} 5 &&\; =\;&& s\cdot120{,}2 &&\; -\;&& t\cdot100 \\ 10 &&\; =\;&& s\cdot96{,}4 &&\; -\;&& t\cdot80\\ 0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 \end{alignat}\right\vert$

und du multiplizierst die erste Zeile mit $4$, die zweite Zeile mit $5$:

$\left\vert\begin{alignat}{7} 20 &&\; = \;&& s\cdot480{,}8 &&\; -\;&& t\cdot400 \\ 50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ 0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 \end{alignat}\right\vert$

Nun subtrahiere die zweite Zeile von der ersten Zeile:

$\left\vert\begin{alignat}{7} {-}30 &&\; = \;&& s\cdot{-}1{,}2 \\ 50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ 0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 \end{alignat}\right\vert$

also folgt:

$\left\vert\begin{alignat}{7} 25 &&\; = \;&& s \\ 50 &&\; =\;&& s\cdot482 &&\; -\;&& t\cdot400\\ 0 &&\; =\;&& s\cdot84 &&\; -\;&& t\cdot70 \end{alignat}\right\vert$

Du erhälst also $s=25$. Wenn du dies in die zweite Zeile einsetzt und umformst, erhälst du: $\left\vert\begin{alignat}{7} 25 &&\; = \;&& s \\ 30 &&\; =\;&& t \\ 0 &&\; =\;&& 25\cdot84 &&\; -\;&& t\cdot70 \end{alignat}\right\vert$

Setzen wir nun in die letzte Zeile $t=30$ ein, so erhalten wir dort $0=0$ und wissen damit, dass sich die Geraden schneiden.

Da es jedoch nicht der gleiche Zeitpunkt ist, kommt es zu keiner Kollision.