Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 92: | Zeile 92: | ||
2. Berechne den Abstand, indem du die Koordinaten des Punktes <math>P(p_1|p_2|p_3)</math> in die Formel einsetzt: | 2. Berechne den Abstand, indem du die Koordinaten des Punktes <math>P(p_1|p_2|p_3)</math> in die Formel einsetzt: | ||
<math> | <math>d(P;E)=\frac {|a\cdot p_1+b\cdot p_2+c\cdot p_3-d|}{|\vec{n}|}</math>| Merksatz}} | ||
Die folgenden Aufgaben kannst du entweder mit dem Lotfußpunktverfahren oder der Formel für den Abstand eines Punktes von einer Ebene lösen. Bei der Klapplösung werden jeweils beide Lösungswege aufgeführt. | Die folgenden Aufgaben kannst du entweder mit dem Lotfußpunktverfahren oder der Formel für den Abstand eines Punktes von einer Ebene lösen. Bei der Klapplösung werden jeweils beide Lösungswege aufgeführt. | ||
| Zeile 114: | Zeile 114: | ||
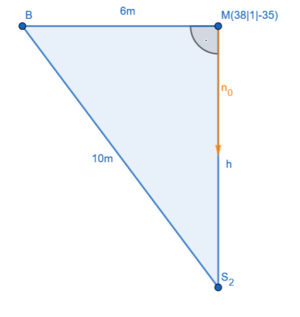
Die Koordinaten von <math>B</math> können in die selbe Formel eingesetzt werden: <math>\frac {|8\cdot(-1)-4\cdot7-1\cdot4-5|}{9}=\frac {|-8-28-4-5|}{9}=\frac {|-45|}{9}=5</math>. | Die Koordinaten von <math>B</math> können in die selbe Formel eingesetzt werden: <math>\frac {|8\cdot(-1)-4\cdot7-1\cdot4-5|}{9}=\frac {|-8-28-4-5|}{9}=\frac {|-45|}{9}=5</math>. | ||
Damit hat die Drohne von Anton einen Abstand von <math>\frac{2}{3} LE</math> zum Schuldach und die Drohne von Bianca einen Abstand von <math>5 | Damit hat die Drohne von Anton einen Abstand von <math>\frac{2}{3} LE</math> zum Schuldach und die Drohne von Bianca einen Abstand von <math>5</math>LE. Antons Drohne ist also näher zum Dach als Biancas Drohne. | ||
|2=Lösungsweg anzeigen|3=Lösungsweg verbergen}} | |2=Lösungsweg anzeigen|3=Lösungsweg verbergen}} | ||
{{Lösung versteckt|1=Der Abstand der Drohne von Anton zum Dach beträgt <math>\frac{2}{3} | {{Lösung versteckt|1=Der Abstand der Drohne von Anton zum Dach beträgt <math>\frac{2}{3}</math>LE und der Abstand von Biancas Drohne zum Dach beträgt <math>5</math>LE. Damit ist der Abstand von Antons Drohne geringer.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Farbe={{Farbe|orange}} }} | | Farbe={{Farbe|orange}} }} | ||
Version vom 30. Mai 2021, 13:38 Uhr
Einstieg
Je nachdem, bei welchem Abstandsproblem du hier noch Schwierigkeiten hattest oder was du einfach noch üben willst, kannst du dir den jeweiligen Abschnitt dieses Lernpfadkapitels anschauen.
Abstand eines Punktes von einer Ebene
Die folgenden Aufgaben kannst du entweder mit dem Lotfußpunktverfahren oder der Formel für den Abstand eines Punktes von einer Ebene lösen. Bei der Klapplösung werden jeweils beide Lösungswege aufgeführt.
Abstand eines Punktes von einer Geraden
Abstand zweier windschiefer Geraden