Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 25: | Zeile 25: | ||
}} | }} | ||
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, | Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, kannst du [https://www.youtube.com/watch?v=cCetvDxbTQk hier] noch einmal nachvollziehen. | ||
{{Box | {{Box | ||
| Zeile 42: | Zeile 40: | ||
'''b)''' <math>A(-3|{-}2|9), B(0|0|3)</math> | '''b)''' <math>A(-3|{-}2|9), B(0|0|3)</math> | ||
Wie du im obigen Video gesehen hast, gibt es unendlich viele Lösungen, denn es sind immer Vielfache des Richtungsvektors möglich. Daher ist es möglich, dass deine Lösung hier zwar nicht aufgefürt, aber dennoch korrekt ist. Dazu überprüfe, ob dein Richtungsvektor ein Vielfaches einer der angegeben Richtungsvektoren ist. Beachte das auch bei allen folgenden Aufgaben! | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ | |Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -6 \\ 5 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g \colon \vec{x} = \begin{pmatrix} 5 \\ -4 \\ 7 \end{pmatrix} + t \cdot \begin{pmatrix} -4 \\ 6 \\ -5 \end{pmatrix}, t \in \mathbb{R} </math>. | ||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 50: | Zeile 50: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} -3 \\ - | |Zwei mögliche Geraden sind <math>g \colon \vec{x} = \begin{pmatrix} -3 \\ -2 \\ 9 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}, s \in \mathbb{R} </math> und <math>g \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \\ 6 \end{pmatrix}, t \in \mathbb{R} </math>. | ||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 64: | Zeile 64: | ||
{{Box | {{Box | ||
|Aufgabe 2: Geradengleichung aufstellen | |Aufgabe 2: Geradengleichung aufstellen auf Punkt und Richtungsvektor | ||
|Stelle jeweils eine Geradengleichung auf. | |Stelle jeweils eine Geradengleichung auf. | ||
'''a)''' Die Gerade <math>g</math> geht durch den Punkt <math>P( | '''a)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(1|{-}1|2)</math> und hat den Richtungsvektor <math>\vec{v} = \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}</math>. | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Überlege dir wie der Stützvektor der Geraden lauten muss und stelle dann die passende Geradengleichung mit dem Richtungsvektor auf. | ||
|Tipp Aufgabe a) anzeigen | |Tipp Aufgabe a) anzeigen | ||
|Tipp Aufgabe a) verbergen | |Tipp Aufgabe a) verbergen | ||
}} | }} | ||
'''b)''' | '''b)''' Stelle eine Geradengleichung für die <math>x_1</math>-Achse auf. | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Überlege dir einen geschickten Aufpunkt; wie muss dann der Richtungsvektor aussehen? | ||
|Tipp Aufgabe b) anzeigen | |Tipp Aufgabe b) anzeigen | ||
|Tipp Aufgabe b) verbergen | |Tipp Aufgabe b) verbergen | ||
}} | }} | ||
'''c)''' Die Gerade <math>g</math> geht durch den einen beliebigen Punkt <math>P(p_1|p_2|p_3)</math> und verläuft parallel zur <math>x_3</math>-Achse. | '''c)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(2|{-}2|4)</math> und verläuft parallel zur Geraden <math>h: \vec{x} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, r \in \mathbb{R} </math>. | ||
{{Lösung versteckt | |||
|Wann verlaufen zwei Vektoren parallel zueinander? Übertrage diese Kenntniss auf Geraden. | |||
|Tipp Aufgabe c) anzeigen | |||
|Tipp Aufgabe c) verbergen | |||
}} | |||
'''d)''' Die Gerade <math>g</math> geht durch den Punkt <math>P(1|{-}1|{-}2)</math> und verläuft parallel zur <math>x_1</math>-Achse. | |||
'''e)''' Die Gerade <math>g</math> geht durch den einen beliebigen Punkt <math>P(p_1|p_2|p_3)</math> und verläuft parallel zur <math>x_3</math>-Achse. | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|Diese Aufgabe funktioniert ähnlich zu | |Diese Aufgabe funktioniert ähnlich zu d). | ||
|Tipp Aufgabe | |Tipp Aufgabe e) anzeigen | ||
|Tipp Aufgabe | |Tipp Aufgabe e) verbergen | ||
}} | }} | ||
| Zeile 94: | Zeile 104: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} | |Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}, s \in \mathbb{R} </math>. | ||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 100: | Zeile 110: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math> | |Eine mögliche Gerade ist <math>x_1 \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math> oder noch einfacher <math>x_1 \colon \vec{x} = s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math> | ||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 106: | Zeile 116: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} | |Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, s \in \mathbb{R} </math>. | ||
|Lösung Aufgabe c) anzeigen | |Lösung Aufgabe c) anzeigen | ||
|Lösung Aufgabe c) verbergen | |Lösung Aufgabe c) verbergen | ||
}} | |||
{{Lösung versteckt | |||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R} </math>. | |||
|Lösung Aufgabe d) anzeigen | |||
|Lösung Aufgabe d) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Eine mögliche Gerade ist <math>g \colon \vec{x} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, s \in \mathbb{R} </math>. | |||
|Lösung Aufgabe e) anzeigen | |||
|Lösung Aufgabe e) verbergen | |||
}} | }} | ||
| Zeile 116: | Zeile 138: | ||
===Punktprobe=== | ===Punktprobe=== | ||
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade | Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du [https://www.youtube.com/watch?v=1kJ9Nq8zXlI hier] noch einmal nachschauen. | ||
{{Box | {{Box | ||
| Zeile 157: | Zeile 177: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Die Punktprobe ist nicht erfüllt, | |Die Punktprobe ist nicht erfüllt, denn: | ||
<math>\begin{pmatrix} 2 \\ -1 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 3 \\ 3 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
2 &&\; = \;&& 1 &&\; + \;&& r \\ | |||
-1 &&\; = \;&& 0 &&\; + \;&& 3r \\ | |||
-1 &&\; = \;&& 1 &&\; + \;&& 3r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 1 \\ | |||
r &&\; = \;&& -frac{1}{3} \\ | |||
r &&\; = \;&& -frac{2}{3} | |||
\end{alignat}\right\vert</math> | |||
Es ergibt sich ein Widerspruch. Somit liegt der Punkt <math>P</math> nicht auf der Geraden <math>g</math>. | |||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 168: | Zeile 204: | ||
{{Box | {{Box | ||
|Aufgabe 4: Punktprobe mit einer Geraden II | |Aufgabe 4: Punktprobe mit einer Geraden II | ||
|Für | |Für welche Werte <math>s, r</math> mit <math> s, r \in \mathbb{R} </math> liegt der Punkt <math>P</math> auf der Geraden <math>g: \vec{x} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} </math>? | ||
'''a)''' <math>P(13|3|0)</math> | '''a)''' <math>P(13|3|0)</math> | ||
'''b)''' <math>P( | '''b)''' <math>P(5|{-}2|0)</math> | ||
{{Lösung versteckt | |||
|Berechne zunächst mithilfe der ersten Gleichung einen Wert für <math>r</math>. Was könnte man nun machen? | |||
|Tipp 1 Aufgabe a) und b) anzeigen | |||
|Tipp 1 Aufgabe a) und b) verbergen | |||
}} | |||
{{Lösung versteckt | |||
|Setze nun den ausgerechneten Wert für <math>r</math> in die beiden anderen Gleichungen ein und berechne <math>s</math>. | |||
|Tipp 2 Aufgabe a) und b) anzeigen | |||
|Tipp 2 Aufgabe a) und b) verbergen | |||
}} | |||
{{Lösung versteckt | {{Lösung versteckt | ||
|Die Punktprobe ist | |Die Punktprobe ist erfüllt, denn: | ||
<math>\begin{pmatrix} 13 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
13 &&\; = \;&& 9 &&\; + \;&& 2r \\ | |||
3 &&\; = \;&& -s &&\; + \;&& r \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
3 &&\; = \;&& -s &&\; + \;&& 2 \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& 2 | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
s &&\; = \;&& -1 \\ | |||
s &&\; = \;&& -1 | |||
\end{alignat}\right\vert</math> | |||
Somit liegt der Punkt <math>P</math> auf der Geraden <math>g</math>. | |||
|Lösung Aufgabe a) anzeigen | |Lösung Aufgabe a) anzeigen | ||
|Lösung Aufgabe a) verbergen | |Lösung Aufgabe a) verbergen | ||
| Zeile 181: | Zeile 250: | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |Es gibt keine Lösung, denn: | ||
<math>\begin{pmatrix} 5 \\ -2 \\ 0 \end{pmatrix} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
5 &&\; = \;&& 9 &&\; + \;&& 2r \\ | |||
-2 &&\; = \;&& -s &&\; + \;&& r \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& r | |||
\end{alignat}\right\vert | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& -2 \\ | |||
-2 &&\; = \;&& -s &&\; + \;&& -2 \\ | |||
0 &&\; = \;&& 2s &&\; + \;&& -2 | |||
\Leftrightarrow\left\vert\begin{alignat}{7} | |||
r &&\; = \;&& 2 \\ | |||
s &&\; = \;&& 0 \\ | |||
s &&\; = \;&& 1 | |||
\end{alignat}\right\vert</math> | |||
Es ergibt sich ein Widerspruch, weshalb keine Werte für Punkt <math>s, r</math> gibt, sodass der Punkt <math>P</math> auf der Geraden <math>g</math> liegt. | |||
|Lösung Aufgabe b) anzeigen | |Lösung Aufgabe b) anzeigen | ||
|Lösung Aufgabe b) verbergen | |Lösung Aufgabe b) verbergen | ||
| Zeile 188: | Zeile 278: | ||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem: | |||
{{Box | |||
|Aufgabe 5: Besondere Geraden im Raum | |||
|Kreuze alle(!) richtigen Antworten an! | |||
{{LearningApp|width=100%|height=500px|app=p221zv0i321}} | |||
|Arbeitsmethode | |||
|Farbe={{Farbe|grün|dunkel}} | |||
}} | |||
===Spurpunkte einer Geraden=== | ===Spurpunkte einer Geraden=== | ||
Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, | Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du [https://www.youtube.com/watch?v=OCO28fT5Aww hier] noch einmal nachvollziehen. | ||
Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen: | Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen: | ||
| Zeile 202: | Zeile 304: | ||
}} | }} | ||
Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du die Punkte <math>A</math> und <math>B</math> anpassen, durch die die Gerade verlaufen soll. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen: | |||
<ggb_applet id="KrHVKfjB" width="900" height="402" border="888888" /> | |||
{{Box | {{Box | ||
| | |Aufgabe 6: Spurpunkte einer Geraden | ||
| | |Berechne die Spurpunkte der Geraden <math>g</math>. | ||
'''a)''' 3 Spurpunkte | |||
'''b)'''<math>g \colon \vec{x} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}, r \in \mathbb{R} </math> | |||
'''c)''' 1 Spurpunkt oder unendlich | |||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |... | ||
| | |Lösung Aufgabe a) anzeigen | ||
| | |Lösung Aufgabe a) verbergen | ||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
|Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene: <math>\vec{S_{13}} = \begin{pmatrix} 1 \\ - | |# Für den Schnittpunkt <math>S_{12}</math> der Geraden <math>g</math> mit der <math>x_1x_2</math>-Ebene setze die <math>x_3</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 2 + r \cdot 1 \Leftrightarrow r = -2</math>. Setze nun <math>r = -2</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{12}</math> zu erhalten: <math>\vec{S_{12}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -8 \\ 0 \end{pmatrix}</math>. | ||
# Für den Schnittpunkt <math>S_{13}</math> der Geraden <math>g</math> mit der <math>x_1x_3</math>-Ebene setze die <math>x_2</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = -4 + r \cdot 2 \Leftrightarrow r = 2</math>. Setze nun <math>r = 2</math> in der Geradengleichung ein, um den Schnittpunkt <math>S_{13}</math> zu erhalten: <math>\vec{S_{13}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix}</math> | |||
# Für den Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene setze die <math>x_1</math>-Koordinate <math>= 0</math> und forme nach <math>r</math> um: <math>0 = 1 + r \cdot 0 \Leftrightarrow 0 = 1</math>. Es ergibt sich ein Widerspruch, weshalb es keinen Schnittpunkt <math>S_{23}</math> der Geraden <math>g</math> mit der <math>x_2x_3</math>-Ebene gibt. Somit verläuft <math>g</math> parallel zur <math>x_2x_3</math>-Ebene. | |||
|Lösung Aufgabe b) anzeigen | |||
|Lösung Aufgabe b) verbergen | |||
}} | }} | ||
{{Lösung versteckt | {{Lösung versteckt | ||
| | |... | ||
| | |Lösung Aufgabe c) anzeigen | ||
| | |Lösung Aufgabe c) verbergen | ||
}} | }} | ||
|Hervorhebung1 | |||
| | |||
}} | }} | ||
==Lagebeziehungen von Geraden== | ==Lagebeziehungen von Geraden== | ||
Version vom 30. Mai 2021, 13:06 Uhr
Geraden und ihre Darstellungsformen
Parameterdarstellung einer Geraden
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, kannst du hier noch einmal nachvollziehen.
Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.
Punktprobe
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade oder daneben liegt, kannst du hier noch einmal nachschauen.
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:
Spurpunkte einer Geraden
Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, kannst du hier noch einmal nachvollziehen.
Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen:
Die -Ebene ist die Ebene, die von der - und -Achse aufgespannt wird (im Bild genannt). Entsprechendes gilt für die - (im Bild ) und -Ebene (im Bild ).
Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du die Punkte und anpassen, durch die die Gerade verlaufen soll. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen:

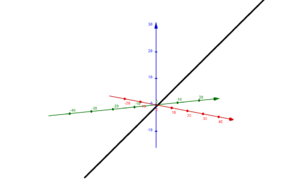
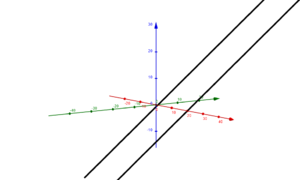
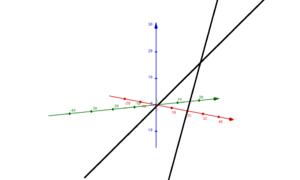
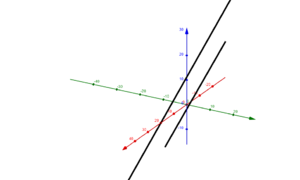
Lagebeziehungen von Geraden
Parallele und identische Geraden