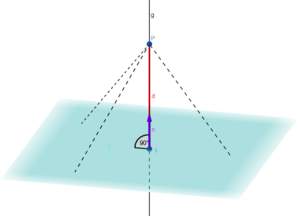
Betrachte das Dreieck  . Es sind die Punkte
. Es sind die Punkte  und
und  gegeben, durch sie verläuft die Gerade
gegeben, durch sie verläuft die Gerade  . Der Punkt
. Der Punkt  liegt auf der zu
liegt auf der zu  parallelen Geraden
parallelen Geraden  .
.
a) Stimmt die Behauptung "Der Flächeninhalt des Dreiecks  ändert sich, je nachdem wo
ändert sich, je nachdem wo  auf der Geraden
auf der Geraden  liegt"? Wenn ja, warum? Wenn nein, warum nicht?
liegt"? Wenn ja, warum? Wenn nein, warum nicht?
Du kannst mit der Maus den Punkt  verschieben.
verschieben.
Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man

verschiebt?
Die Behauptung stimmt nicht. Den Flächeninhalt Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}}
eines Dreiecks kann man bekanntermaßen mit der Formel Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h}
berechnen, wobei  die Länge der Grundseite ist.
die Länge der Grundseite ist.
In dieser Aufgabe bleibt der Abstand

immer gleich, da sich

auf einer zu

parallelen Geraden "bewegt". Also ist die Höhe

all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h}
nicht.
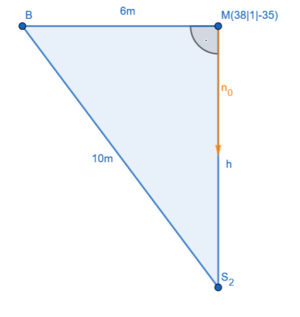
b) Bestimme den Flächeninhalt des Dreicks  .
.
Überlege dir, welche Abstände du berechnen musst, um den Flächeninhalt bestimmen zu können.
Der Flächeninhalt des Dreiecks beträgt ungefähr  Flächeneinheiten.
Flächeneinheiten.
Ein möglicher Lösungsweg:
Wir bestimmen zunächst die Länge  der Grundseite:
Es
der Grundseite:
Es  .
.
Nun bestimmen wir die Höhe  , also den Abstand der parallelen Geraden
, also den Abstand der parallelen Geraden  und
und  mithilfe des Verbindungsvektors von
mithilfe des Verbindungsvektors von  zur Geraden
zur Geraden  .(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten):
.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten):
Der Punkt  ist ein allgemeiner Punkt auf
ist ein allgemeiner Punkt auf  . Ein allgemeiner Verbindungsvektor zwischen
. Ein allgemeiner Verbindungsvektor zwischen  und
und  ist also gegeben durch
ist also gegeben durch  .
.
Damit  orthogonal zum Richtungsvektor von
orthogonal zum Richtungsvektor von  ist, muss gelten:
ist, muss gelten:
 bzw.
bzw.  . Es folgt
. Es folgt  , also ist der Verbindungsvektor für
, also ist der Verbindungsvektor für  am kürzesten. Somit ist
am kürzesten. Somit ist  .
.
Der Flächeninhalt des Dreiecks beträgt also
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h=\frac{1}{2}\cdot \sqrt{58,5} \cdot 5\approx 19,12}
Flächeneinheiten.