Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 79: | Zeile 79: | ||
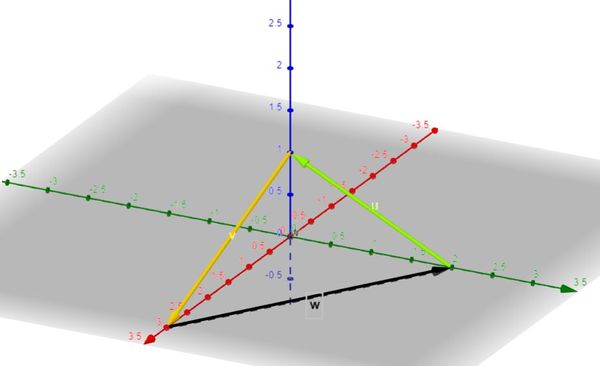
# <math>\vec{0A} - \vec{u}-\vec{w}-\vec{v} </math> | # <math>\vec{0A} - \vec{u}-\vec{w}-\vec{v} </math> | ||
# <math>\vec{0C} - \vec{u}+\vec{u}</math> | # <math>\vec{0C} - \vec{u}+\vec{u}</math> | ||
# <math>\vec{0B} + 2 | # <math>\vec{0B} + 2 \cdot \vec{u} + 2 \cdot \vec{v} + \vec{w} </math> | ||
Version vom 30. Mai 2021, 09:25 Uhr
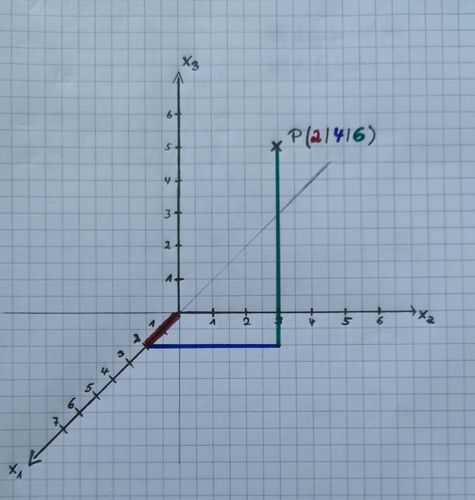
Wiederholung von Punkten und Vektoren