Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 19: | Zeile 19: | ||
{{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | {{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. | ||
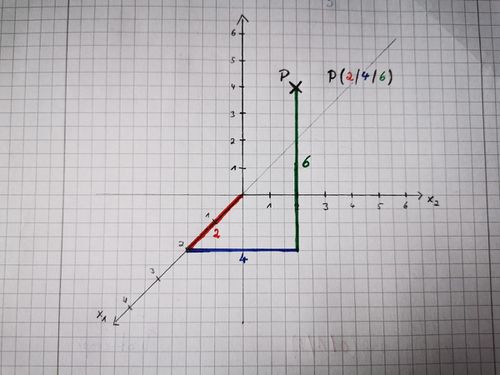
# Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | # Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. | ||
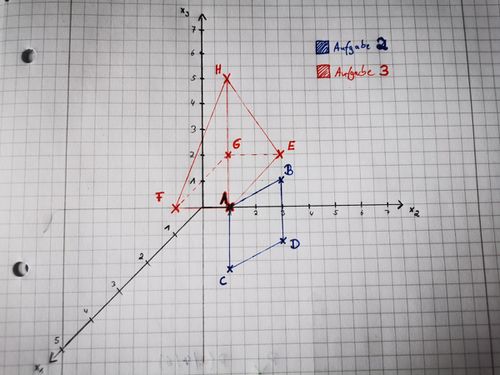
# Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|-1,5)</math> und <math> D(1|4|-0,5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Strecken <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | # Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1,5)</math> und <math> D(1|4|{-}0,5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Strecken <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
# Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Strecken <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ AH }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> und <math>\vec{ GH }</math>. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | # Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Strecken <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ AH }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. | ||
| Zeile 141: | Zeile 141: | ||
- <math> 6,5 </math> | - <math> 6,5 </math> | ||
{<math> A(-1|-2|2) </math> und <math> B(-3|-1|0) </math>} | {<math> A(-1|{-}2|2) </math> und <math> B(-3|{-}1|0) </math>} | ||
+ <math> 3 </math> | + <math> 3 </math> | ||
- <math> 6 </math> | - <math> 6 </math> | ||
| Zeile 193: | Zeile 193: | ||
- <math> P(7|4|3)</math> | - <math> P(7|4|3)</math> | ||
+ <math> P(0|4|3)</math> | + <math> P(0|4|3)</math> | ||
- <math> P(6|3|-1)</math> | - <math> P(6|3|{-}1)</math> | ||
</quiz> | </quiz> | ||
{{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist. |2=Tipp 1|3=Tipp verbergen}} | {{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist. |2=Tipp 1|3=Tipp verbergen}} | ||
| Zeile 201: | Zeile 201: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{c) Sei <math> P </math> nun ein weiter Punkt im bereits vorhandenen System. Welche Koordinaten muss <math> P </math> haben, damit <math> P </math> gemeinsam mit <math> A </math>, <math> B </math> und <math> C </math> die Eckpunkte einer Raute bildet?} | {c) Sei <math> P </math> nun ein weiter Punkt im bereits vorhandenen System. Welche Koordinaten muss <math> P </math> haben, damit <math> P </math> gemeinsam mit <math> A </math>, <math> B </math> und <math> C </math> die Eckpunkte einer Raute bildet?} | ||
+ <math> P(7|3|-1)</math> | + <math> P(7|3|{-}1)</math> | ||
- <math> P(-7|-3|1)</math> | - <math> P(-7|{-}3|1)</math> | ||
- <math> P(5|2|-3)</math> | - <math> P(5|2|{-}3)</math> | ||
- <math> P(-5|-2|3)</math> | - <math> P(-5|{-}2|3)</math> | ||
</quiz> | </quiz> | ||
{{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist.|2=Tipp 1|3=Tipp verbergen}} | {{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist.|2=Tipp 1|3=Tipp verbergen}} | ||
Version vom 29. Mai 2021, 15:24 Uhr
Wiederholung von Punkten und Vektoren