Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 213: | Zeile 213: | ||
|2=Lösung anzeigen|3=Lösung verbergen}} | |2=Lösung anzeigen|3=Lösung verbergen}} | ||
<ggb_applet id="qu6yfdp6" width=100% height=100%/> | <ggb_applet id="qu6yfdp6" width=100% height=100%/> | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
| Zeile 369: | Zeile 370: | ||
{{Box | 1=Aufgabe 11: Dreieck | 2= | {{Box | 1=Aufgabe 11: Dreieck | 2= | ||
Es sind die Punkte <math>B(2|8|1) </math> und <math>C(0,5|3,5|7) </math> gegeben, durch sie verläuft die Gerade <math> | Betrachte das Dreieck <math>DBC</math>. Es sind die Punkte <math>B(2|8|1) </math> und <math>C(0,5|3,5|7) </math> gegeben, durch sie verläuft die Gerade <math> i </math>. Der Punkt <math>D</math> liegt auf der zu <math> i </math> parallelen Geraden <math> j:\vec{x}= \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}+t\cdot\begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix} </math>. | ||
'''a)''' Stimmt die Behauptung "Der Flächeninhalt des Dreiecks <math> | '''a)''' Stimmt die Behauptung "Der Flächeninhalt des Dreiecks <math>DBC</math> ändert sich, je nachdem wo <math>D</math> auf der Geraden <math>j</math> liegt"? Wenn ja, warum? Wenn nein, warum nicht? | ||
Du kannst mit der Maus den Punkt <math> | Du kannst mit der Maus den Punkt <math>D</math> verschieben. | ||
<ggb_applet id="mftwqmc8" width=50%" height="658"/> | <ggb_applet id="mftwqmc8" width=50%" height="658"/> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man <math> | Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man <math>D</math> verschiebt? | ||
|2=Tipp zu a)anzeigen|3=Tipp zu a) verbergen}} | |2=Tipp zu a)anzeigen|3=Tipp zu a) verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Behauptung stimmt nicht. Den Flächeninhalt <math> | Die Behauptung stimmt nicht. Den Flächeninhalt <math>A_{text{DBC}}</math> eines Dreiecks kann man bekanntermaßen mit der Formel <math>A_{text{DBC}}=\frac{1}{2}\cdot g \cdot h</math> berechnen, wobei <math>g</math> die Länge der Grundseite ist. | ||
In dieser Aufgabe bleibt der Abstand <math>d( | In dieser Aufgabe bleibt der Abstand <math>d(D;i)</math> immer gleich, da sich <math>D</math> auf einer zu <math>i</math> parallelen Geraden "bewegt". Also ist die Höhe <math>h</math> all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt <math>A_{text{DBC}}=\frac{1}{2}\cdot g \cdot h</math> nicht. | ||
|2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | |2=Lösung zu a) anzeigen|3=Lösung zu a) verbergen}} | ||
'''b)''' Bestimme den Flächeninhalt des Dreicks <math> | '''b)''' Bestimme den Flächeninhalt des Dreicks <math>DBC</math>. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 391: | Zeile 392: | ||
|2=Tipp zu b)anzeigen|3=Tipp zu b) verbergen}} | |2=Tipp zu b)anzeigen|3=Tipp zu b) verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Flächeninhalt des Dreiecks beträgt ungefähr <math>19,12</math> Flächeneinheiten. | |||
Der Lösungsweg: | |||
Wir bestimmen zunächst die Länge <math>g</math> der Grundseite: | |||
Es <math>|\vec{BC}|=\sqrt{(2-0,5)^2+(8-3,5)^2+(1-7)^2}=\sqrt{58,5}</math>. | |||
Nun bestimmen wir die Höhe <math>h</math>, also den Abstand der parallelen Geraden <math>i</math> und <math>j</math> mithilfe des Verbindungsvektors von <math>B</math> zur Geraden <math>j</math>.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten): | |||
Der Punkt <math>L_t=(1+t|1+3t|2-4t)</math> ist ein allgemeiner Punkt auf <math>j</math>. Ein allgemeiner Verbindungsvektor zwischen <math>B</math> und <math>j</math> ist also gegeben durch <math>\vec{BL_t}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}</math>. | |||
<math>\begin{pmatrix} | |||
Der Flächeninhalt des Dreiecks beträgt also <math> | Damit <math>\vec{BL_t}</math> orthogonal zum Richtungsvektor von <math>j</math> ist, muss gelten: | ||
<math>\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\ast \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0 </math> bzw. <math>(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)=0</math>. Es folgt <math>t=1</math>, also ist der Verbindungsvektor für <math>L(2|4|-2)</math> am kürzesten. Somit ist <math>h=d(B;j)=|\vec{BL}|=\sqrt{(2-2)^2+(4-8)^2+(-2-1)^2}=\sqrt{25}=5</math>. | |||
Der Flächeninhalt des Dreiecks beträgt also <math>A_{text{DBC}}=\frac{1}{2}\cdot g \cdot h=\frac{1}{2}\cdot \sqrt{58,5} \cdot 5\approx 19,12</math> Flächeneinheiten. | |||
|2=Möglichen Lösungsweg anzeigen|3=Lösungsweg verbergen}} | |2=Möglichen Lösungsweg anzeigen|3=Lösungsweg verbergen}} | ||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
Version vom 29. Mai 2021, 09:04 Uhr
Einstieg
Je nachdem, bei welchem Abstandsproblem du hier noch Schwierigkeiten hattest oder was du einfach noch üben willst, kannst du dir den jeweiligen Abschnitt dieses Lernpfadkapitels anschauen.
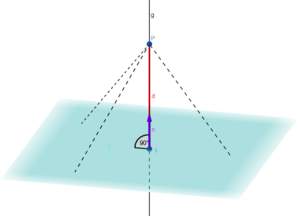
Abstand eines Punktes von einer Ebene
Abstand eines Punktes von einer Geraden
Abstand zweier windschiefer Geraden
Verschiebe die Punkte und so, dass die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden und ist. Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten.