Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum

Info

In diesem Lernpfadkapitel beschäftigst du dich mit Geraden im Raum. Du lernst, Geraden im Raum durch Vektoren zu beschreiben, Parameterdarstellungen und Spurpunkte von Geraden zu bestimmen, die Lage von Geraden im Raum und zueinander zu bestimmen sowie Geradenscharen zu bestimmen.

Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit und
• Aufgaben mit grünem Streifen sind Knobelaufgaben.

Wir wünschen dir viel Erfolg!

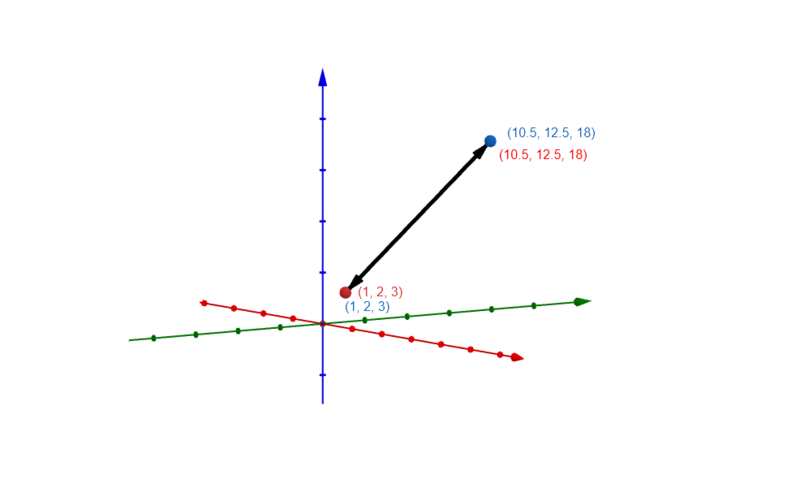
Geraden und ihre Darstellungsformen

Parameterdarstellung einer Geraden

Definition

Jede Gerade lässt sich durch eine Gleichung der Form $g \colon \vec{x} = \vec{OA} + k \cdot \vec{v}$ mit $k \in \mathbb{R}$ beschreiben.

• Diese Vektorgleichung bezeichnet man als Parameterdarstellung oder Parametergleichung der Geraden $g$ mit dem Parameter $k$.
• Setzt man für $k$ irgendeine Zahl in die Parameterdarstellung der Geraden $g$ ein, so ergibt sich der Ortsvektor $\vec{x}$ (auch $\vec{OX}$ genannt) eines Punktes $X$ der Geraden $g$.
• Der Vektor $\vec{OA}$ heißt Stützvektor. Er ist der Ortsvektor zu einem Punkt $A$ (auch Aufpunkt genannt), der auf der Geraden $g$ liegt.
• Der Vektor $\vec{v} \neq \vec{o}$ heißt Richtungsvekor.

Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, wird im folgenden Video erklärt:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

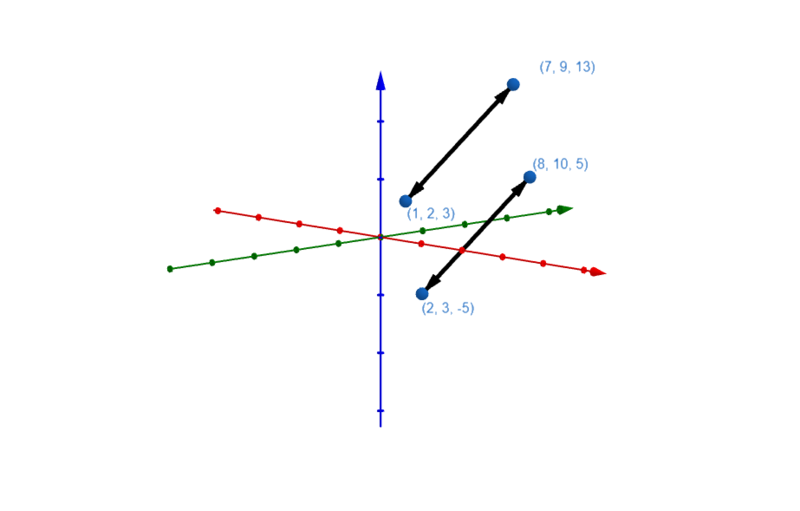
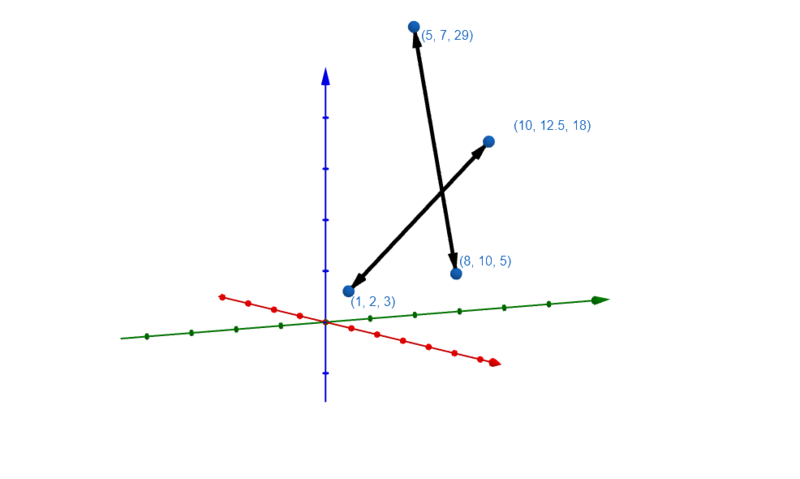
Im Folgenden kannst du sehen, wie die Gerade vom Stützvektor, Richtungsvektor und Parameter abhängt:

 ????Anmerkung zu den Lösungen: Wie du wahrscheinlich im obigen Video mitbekommen hast, gibt es unendlich viele Lösungen. Daher sind auch Vielfache der Richtungsvektoren oder andere Stützvektoren, wenn sie auf der Geraden $g$ liegen, möglich.????

Aufgabe 1: Geradengleichung aufstellen (zwei gegebene Punkte)

Bearbeite entweder die analoge Aufgabe (I) oder die digitale Aufgabe (II):

(I) Die Gerade $g$ geht durch die Punkte $A$ und $B$. Gib zwei Gleichungen für $g$ an.

a) $A(1|2|2), B(5|{-}4|7)$

b) $A(-3|{-}2|9), B(0|0|3)$

Zwei mögliche Geraden sind $g \colon \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 22 \end{pmatrix} + s \cdot \begin{pmatrix} 4 \\ -6 \\ 5 \end{pmatrix}, s \in \mathbb{R}$ und $g \colon \vec{x} = \begin{pmatrix} 5 \\ -4 \\ 7 \end{pmatrix} + t \cdot \begin{pmatrix} -4 \\ 6 \\ -5 \end{pmatrix}, t \in \mathbb{R}$.

Zwei mögliche Geraden sind $g \colon \vec{x} = \begin{pmatrix} -3 \\ -3 \\ 9 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ 2 \\ -6 \end{pmatrix}, s \in \mathbb{R}$ und $g \colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \\ 6 \end{pmatrix}, t \in \mathbb{R}$.

(II) Ordne jeweils die zwei Punkte A und B der Parametergleichung der Geraden durch A und B zu.

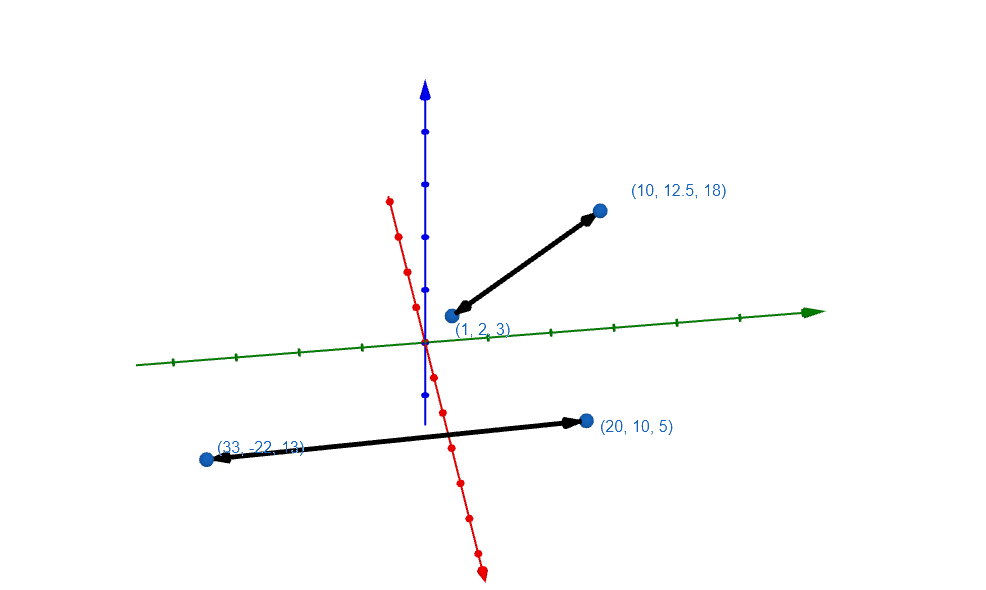
Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt $P$ verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.

Aufgabe 2: Geradengleichung aufstellen (gegebener Punkt und gegeben Parallelität)

Stelle jeweils eine Geradengleichung auf.

a) Die Gerade $g$ geht durch den Punkt $P(2|{-}2|4)$ und verläuft parallel zur geraden $h: \vec{x} = \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, r \in \mathbb{R}$.

Wann verlaufen zwei Vektoren parallel zueinander? Übertrage diese Kenntniss auf Geraden.

b) Die Gerade $g$ geht durch den Punkt $P(1|{-}1|{-}2)$ und verläuft parallel zur $x_1$-Achse.

Wie könnte eine Geradengleichung der $x_1$-Achse lauten? Danahc hilft dir das Vorgehen aus a) weiter.

c) Die Gerade $g$ geht durch den einen beliebigen Punkt $P(p_1|p_2|p_3)$ und verläuft parallel zur $x_3$-Achse.

Diese Aufgabe funktioniert ähnlich zu b).

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} 2 \\ -2 \\ 4 \end{pmatrix} + s \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}, s \in \mathbb{R}$.

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} 1 \\ -1 \\ -2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, s \in \mathbb{R}$.

Eine mögliche Gerade ist $g \colon \vec{x} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} + s \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, s \in \mathbb{R}$.

Punktprobe

Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade der daneben liegt, erfährst du im folgenden Video:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Merksatz: Punktprobe

Liegt ein Punkt $P$ auf der Geraden g definiert durch $g: \vec{x} = \vec{a} + k \cdot \vec{v}$ mit $k \in \mathbb{R}$, so gibt es genau ein $k$, welches die Gleichung $\vec{p} = \vec{a} + k \cdot \vec{v}, r \in \mathbb{R}$ erfüllt. Erfüllt kein $k$ diese Gleichung, liegt der Punkt nicht auf der Geraden.

Aufgabe 3: Punktprobe mit einer Geraden I

Überprüfe, ob der Punkt $P$ auf der Geraden $g$ liegt.

a) $P(2|3|{-}1), g \colon \vec{x} = \begin{pmatrix} 7 \\ 0 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 5 \\ -3 \\ 5 \end{pmatrix}, r \in \mathbb{R}$

b) $P(2|{-}1|{-}1), g \colon \vec{x} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 3 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die Punktprobe ist erfüllt für $t = -1$, d.h. der Punkt $P$ liegt auf der Geraden $g$.

Die Punktprobe ist nicht erfüllt, d.h. der Punkt $P$ liegt nicht auf der Geraden $g$.

Aufgabe 4: Punktprobe mit einer Geraden II

Für welchen Wert $s$ mit $s \in \mathbb{R}$ liegt der Punkt $P$ auf der Geraden $g: \vec{x} = \begin{pmatrix} 9 \\ -s \\ 2s \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}, r \in \mathbb{R}$?

a) $P(13|3|0)$

b) $P(12|{-}1|6{,}5)$

Die Punktprobe ist für $s = -1$ mit $r = 2$ erfüllt.

Die Punktprobe ist für $s = 2{,}5$ mit $r = 1{,}5$ erfüllt.

Spurpunkte einer Geraden

Wie du die Spurpunkte, also die Schnittpunkte der Geraden mit den Koordinatenebenen bestimmst, zeigt das folgende Video.

Falls du nicht mehr weißt, was die Koordinatenebenen sind, kannst unter folgendem Tipp noch einmal dein Wissen auffrischen:

Die $x_1x_2$-Ebene ist die Ebene, die von der $x_1$- und $x_2$-Achse aufgespannt wird (im Bild $E_{12}$ genannt). Entsprechendes gilt für die $x_1x_3$- (im Bild $E_{13}$) und $x_2x_3$-Ebene (im Bild $E_{23}$).

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Achtung: Nicht jede Gerade besitzt drei Spurpunkte!

Verläuft eine Gerade zu einer der Koordinatenachsen oder -ebenen (echt) parallel, gibt es keinen Schnittpunkt mit der entsprechenden Koordinatenebene. In deiner Rechnung erkennst du es daran, dass es in der Zeile, die du $= 0$ gesetzt hast, keine Lösung für den Parameter gibt.

Beispiel: Gerade mit nur zwei Spurpunkten

Gegeben ist die Gerade $g$ definiert durch $g \colon \vec{x} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}, r \in \mathbb{R}$. Im Folgenden werden die Spurpunkte berechnet (du kannnst es natürlich auch selbst versuchen und dann deine Lösung kontrollieren):

Für den Schnittpunkt $S_{12}$ der Geraden $g$ mit der $x_1x_2$-Ebene setze die $x_3$-Koordinate $= 0$ und forme nach $r$ um: $0 = 2 + r \cdot 1 \Leftrightarrow r = -1$. Setze nun $r = -2$ in der Geradengleichung ein, um den Schnittpunkt $S_{12}$ zu erhalten: $\vec{S_{12}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + (-2) \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -8 \\ 0 \end{pmatrix}$

Für den Schnittpunkt $S_{13}$ der Geraden $g$ mit der $x_1x_3$-Ebene setze die $x_2$-Koordinate $= 0$ und forme nach $r$ um: $0 = -4 + r \cdot 2 \Leftrightarrow r = 2$. Setze nun $r = 2$ in der Geradengleichung ein, um den Schnittpunkt $S_{13}$ zu erhalten: $\vec{S_{13}} = \begin{pmatrix} 1 \\ -4 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix}$

Für den Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene setze die $x_1$-Koordinate $= 0$ und forme nach $r$ um: $0 = 1 + r \cdot 0 \Leftrightarrow 0 \neq 1$. Es ergibt sich ein Widerspruch, weshalb es keinen Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene gibt. Somit verläuft $g$ parallel zur $x_2x_3$-Ebene.

Hier kannst du dir die Spurpunkte von verschiedenen Geraden anzeigen lassen. Dazu kannst du die Punkte $A$ und $B$ anpassen, durch die die Gerade verlaufen soll. Dann kannst du dir die Koordinatebenen mit den verschiedenen Schnittpunkten anzeigen lassen:

Aufgabe 5: Spurpunkte einer Geraden I

Berechne die Spurpunkte der Geraden $g$ definiert durch $g: \vec{x} = \begin{pmatrix} 1 \\ -1 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 1 \\ -2 \end{pmatrix}, r \in \mathbb{R}$.

Schnittpunkt $S_{13}$ der Geraden $g$ mit der $x_1x_3$-Ebene: $\vec{S_{13}} = \begin{pmatrix} 1 \\ -1 \\ 4 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}$

Schnittpunkt $S_{12}$ der Geraden $g$ mit der $x_1x_2$-Ebene: $\vec{S_{12}} = \begin{pmatrix} 1 \\ -1 \\ 4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$

Der Schnittpunkt $S_{23}$ der Geraden $g$ mit der $x_2x_3$-Ebene ist nicht vorhanden, da sich ein Widerspruch in der Gleichung ergibt.

Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:

Aufgabe 6: Geraden im Koordinatensystem

Kreuze die richtige(n) Antwort(en) an!

Lagebeziehungen von Geraden

Parallele und identische Geraden

Definition

Wir unterscheiden die Lage zweier Geraden in identisch, parallel, sich schneidend und windschief zueinander. Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander kollinear (sind Vielfache voneinander), so können die Geraden lediglich identisch oder parallel sein.

Um nun zu untersuchen, ob die Geraden parallel oder identisch sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden identisch. Andernfalls sind die Geraden parallel zueinander.

Aufgabe 7: Lage erkennen

Betrachte de folgenden Geraden g und h. Wie verlaufen die Geraden zueinander? Erkläre, warum hier kaum gerechnet werden muss.

a) $g: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, r \in \mathbb{R}$

b) $g: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

c) $g: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $h: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die erste Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren mit $\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 2 \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}$ ein Vielfaches voneinander (=kollinear) sind. Da beide Ortsvektoren identisch sind, liegt ein Punkt sind die Geraden identisch.

Die zweite Antwort lautet parallel. Die beiden Geraden sind parallel. Während die beiden Richtungsvektoren kollinear, sogar identisch, sind liegt der Ortsvektor von $i_2$ nicht auf der Geraden von$i_1: \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$, mit $r=\begin{pmatrix} 1 \\ 0.5 \\ 0.333 \end{pmatrix}$.

Die dritte Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren identisch sind ($\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$) und der Ortsvektor der einen Gerade auf der anderen Gerade ist: $\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$.

windschiefe und sich schneidene Geraden

Definition

Sind die Richtungsvektoren nicht kollinear, so können die Geraden sich lediglich schneiden oder windschief zueinander verlaufen. Unter sich schneidene Geraden verstehen wir Geraden, die sich in einem Punkt schneiden. Windschiefe Geraden hingegen sind Geraden, die sich wie die parallelen Geraden zwar nicht schneiden, ihre Richtungsvektoren sind jedoch nicht kollinear.

Um nun zu untersuchen, ob sich die Geraden schneiden oder zueinader winschief zueinander sind, müssen wir schauen, ob sich ein Schnittpunkt berechnen lässt. Hierzu setzen wir die Geradengleichungen gleich und formen um. Erhalten wir einen Schnittpunkt S, so schneiden sich die Geraden im Punkt S. Andernfalls sind diese Geraden windschief zueinander.

Aufgabe 8: Lage erkennen

Wie verlaufen die folgenden Geraden zueinander? Nenne, falls vorhanden, den Schnittpunkt.

a)$g_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $g_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

b)$h_1: \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 4 \\ 4 \end{pmatrix}, r \in \mathbb{R}$ und $h_2: \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} 4 \\ 5 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

c)$i_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $i_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die erste Antwort lautet schneiden. Die beiden Geraden schneiden sich im Punkt $\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}$. Dies erhält man, indem man beide Geradengelichungen in ein Gleichungssystem umformt, gleichsetzt und zu r und t umformt:

$1+r*1=2+t*4$

$1+r*2=3+t*5$

$1+r*3=4+t*3$

Dies formen wir um:

$r*1-t*4=1$

$r*2-t*5=2$

$r*3-t*3=3$

Nehmen die erste Zeile mal 2, subtrahieren von der ersten Zeile die zweite Zeile und erhalen für t= 0 und r=1.

Die zweite Antwort lautet schneiden. Die beiden Geradenschneidenich im Ortsvektoren selbst.

Die dritte Antwort lautet windschief. Die beiden Geraden sind windschief zueinander. Dies sehen widaran

$1+r*1=2+t*1$

$1+r*2=3+t*4$

$1+r*3=4+t*3$

Dies formen wir um:

$r*1-t*1=1$

$r*2-t*4=2$

$r*3-t*3=3$

Nehmen die erste Zeile mal 2, subtrahieren von der ersten Zeile die zweite Zeile und erhalen für t= 1/6

daran,

Aufgabe 9: Lage erkennen

Löse das Quiz und mache dir deinen eigenen Lernzettel

Aufgabe 10: Lage zweier Geraden

Löse den Lückentext und mache dir deinen eigenen Lernzettel

Aufgabe 11:

Flugerlaubnis erteilen?

Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen zwei Flugzeuge starten. Hierzu gehört das Flugzeug der Fluglinie Aer. Es startet bei $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}$ und befindet sich nach 5sek auf $\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix}$. Ebenfalls möchte das Flugzeug der Fluglinie Amadeus in die Luft. Dies startet in $\begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix}$. Pro Sekunde legt es eine Strecke von 175,49m zurück und besitzt einen Richtungsvektor von $\begin{pmatrix} 120{,}2 \\ 96{,}4 \\ z \end{pmatrix}$.

Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher. Hilf ihm die Antworten auf folgende Fragen zu finden:

a) Wie lauten die Geradengleichungen der einzelen Flugzeuge?

Zu Aer: Setze alle gegebenen Daten in eine allgemeine Parameterdarstellung ein und forme um.

Zu Amadeus: Um den Richtungsvektor zu berechnen, benötigst du die Forme zur Berechnung der Länge eines Vektoren:

$L=\sqrt[2]{x{2}+y^{2}+z^{2}}$.

b) Wie schnell (in km/h) fliegen die einzelnen Flugzeuge?

Geschwindigkeit kann man in verschiedene Einheiten angeben, z.B.: km/h, m/s etc.. Nachdem du die Länge der Strecke nach einer Sekunde berechnet hast, musst du dies von m/s zu km/h umwandeln.

c) Können alle Flugzeuge starten, ohne dass es zu einer Kollision kommt?

Nur weil sich zwei Geraden schneiden heißt es noch nicht direkt, dass eine Kollision vorherrscht.

Flugzeug Aer: $f_3: \vec{x} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}, t \in \mathbb{R}$

Dies erhalten wir, indem wir folgendes berechnen: $\begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 5\cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}, t \in \mathbb{R}$. Dies schreiben wir in ein Gleichugssystem um und formen es zu x,y,z um:

$510=10+5*x$

$410=10+5*y$

$350= 0+5*z$

Flugzeug Amadeus: $f_1: \vec{x} = \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}, t \in \mathbb{R}$

Dies erhalten wir wie folgt: Wir kennen den Richtungsvektor: $\begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}$. Nun müssen wir z berechnen. Im Text steht, dass das Flugzeug pro Sekunde eine Länge von 175,49m fliegt. Das bedeutet, dass der Richtungsvektor eine Länge von 175,49 beträgt. Dies können wir mit der Formel der Länge eines Vektor berechnen:

$175{,}49=\sqrt[2]{120{,}2^{2}+96{,}4^{2}+z^{2}}$

Indem wir beide Seiten zum Quadart nehemn, entfällt die Wurzel und es folgt:

$175{,}49^{2}=120{,}2^{2}+96{,}4^{2}+z^{2}$

Wir formen zu $z^{2}$ um und ziehen dann die Wurzel. Wir erhalten 83,998 und runden auf 84.

Wobei t für die Zeit in Sekunden steht.

Wir berechnen die Geschwindigkeit, indem wir die Länge des Richtungsvektors berechnen. Dies erfolgt mit der Formel:$L=\sqrt[2]{x{2}+y^{2}+z^{2}}$.

Fugzeug Aer: $L=\sqrt[2]{100{2}+80^{2}+70^{2}}$.

Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle L=145{,}95}} .

Wir erhalten also eine Geschwindigkeit von 145,95 m/s. Es gilt: 3,6km/h=1m/s. Umgerechnet in km/h sind das also:

$145{,}95*3{,}6= 525{,}42$ 525,42km/h.

Flugzeug Amadeus: Das Flugzeug Amadeus legt laut Text nach einer Sekunde eine Strecke von 175,49m zurück. Damit hat es eine Geschwindigkeit von 175,49m/s.Umgerechnet in km/h sind das also:

$175{,}49*3{,}6= 631{,}76$

631,76km/h.

Flugzeug Aer und Amadeus: Sie schneiden sich für $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 30 \cdot \begin{pmatrix} 100 \\ 80 \\ 70 \end{pmatrix}= \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} + 25 \cdot \begin{pmatrix} 120{,}2\\ 96{,}4 \\ 84\end{pmatrix}$. Dies erhalten wir, indem wir beide Funktionen gleichsetzen und in ein Gleichungssystem umformen:

$10+t*100=5+s*120{,}2$

$10+t*80=10+s*96{,}4$

$0+t*70=0+s*84$

Da es jedoch nicht der gleiche Zeitpunkt ist, kommt es zu keiner Kollision.