|
|
| Zeile 23: |
Zeile 23: |
| Es gibt drei Möglichkeiten wie eine Ebenen E und eine Gerade g im Raum zueinander liegen können: | | Es gibt drei Möglichkeiten wie eine Ebenen E und eine Gerade g im Raum zueinander liegen können: |
|
| |
|
| * Die Gerade g liegt in der Ebene E.[[Datei:Lagebeziehung Gerade Ebene LiegtIn2.png|rahmenlos]] | | * Die Gerade g liegt in der Ebene E. |
| * Die Gerade g liegt parallel zur Ebene E.[[Datei:Lagebeziehung Gerade Ebene Parallel1.png|rahmenlos|350x350px]] | | * Die Gerade g liegt parallel zur Ebene E.[[Datei:Parallele Ebenen.png|ohne|rahmenlos]] |
| * Die Gerade g schneidet die Ebene E. | | * Die Gerade g schneidet die Ebene E. [[Datei:Schnittgerade von zwei Ebenen.png|ohne|rahmenlos]] |
| |Merksatz}} | | |Merksatz}} |
| | |
| | Für die Lage einer Gerade g zu einer Ebene E sind 3 Fälle möglich: |
| | <br /> |
| | |
| | *Die Gerade g liegt in der Ebene E. [[Datei:Lagebeziehung Gerade Ebene LiegtIn2.png|rahmenlos]] |
| | *Die Gerade g liegt parallel zur Ebene E. [[Datei:Lagebeziehung Gerade Ebene Parallel1.png|rahmenlos|350x350px]]Die Gerade g und die Ebene E schneiden sich. |
|
| |
|
| <br /> | | <br /> |
| Zeile 44: |
Zeile 50: |
| ===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | | ===⭐Berechnung des Winkels zwischen Gerade und Ebene=== |
|
| |
|
| | {{Box | Merke: Winkel berechnen zwischen Gerade und Ebene | Inhalt | Merksatz}} |
| | |
| | {{Box | Beispiel: Winkel berechnen zwischen Gerade und Ebene | Inhalt | Hervorhebung}} |
| | |
| | {{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}} |
| | |
| | {{Box | Aufgabe <Nummer>: Winkel gesucht | Inhalt | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} |
|
| |
|
| ==Lagebeziehung Ebene-Ebene== | | ==Lagebeziehung Ebene-Ebene== |
| Zeile 84: |
Zeile 97: |
|
| |
|
| ===⭐Berechnung des Winkels zwischen Ebene und Ebene=== | | ===⭐Berechnung des Winkels zwischen Ebene und Ebene=== |
| | |
| | {{Box | Merke: Winkel berechnen zwischen zwei Ebenen | Inhalt | Merksatz}} |
| | |
| | {{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | Inhalt | Hervorhebung}} |
| | |
| | {{Box | Aufgabe <Nummer>: Fehlerbeschreibung | Inhalt | Arbeitsmethode | Farbe={{Farbe|orange}} }} |
| | |
| | {{Box | Aufgabe <Nummer>: Zeltwände | Inhalt | Arbeitsmethode}} |
Version vom 4. Mai 2021, 13:24 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Info
In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
- Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Viel Erfolg!
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Mögliche Lagebeziehung zwischen Gerade und Ebene
Es gibt drei Möglichkeiten wie eine Ebenen E und eine Gerade g im Raum zueinander liegen können:
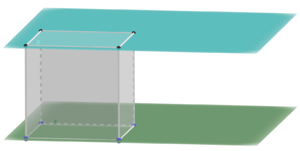
- Die Gerade g liegt in der Ebene E.
- Die Gerade g liegt parallel zur Ebene E.
- Die Gerade g schneidet die Ebene E.
Für die Lage einer Gerade g zu einer Ebene E sind 3 Fälle möglich:
- Die Gerade g liegt in der Ebene E.
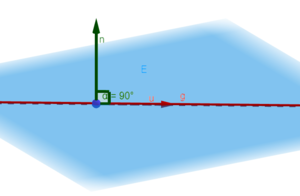
- Die Gerade g liegt parallel zur Ebene E.
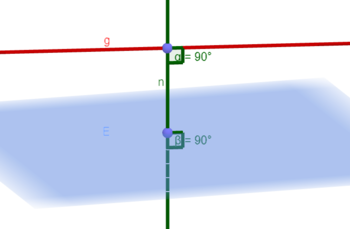 Die Gerade g und die Ebene E schneiden sich.
Die Gerade g und die Ebene E schneiden sich.
Untersuchung der Lagebeziehung
Vorgehen
Beispiel (Ebene in Parameterform)
Übungsaufgaben (Learning App)
Beispiel (Ebene in Koordinatenform)
Übungsaufgaben
⭐Berechnung des Winkels zwischen Gerade und Ebene
Merke: Winkel berechnen zwischen Gerade und Ebene
Inhalt
Beispiel: Winkel berechnen zwischen Gerade und Ebene
Inhalt
Aufgabe <Nummer>: <Name>
Inhalt
Aufgabe <Nummer>: Winkel gesucht
Inhalt
Lagebeziehung Ebene-Ebene
Basiswissen
Lagebeziehung zwischen Ebenen
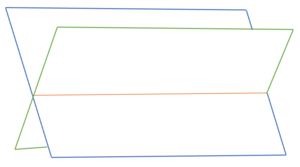
Es gibt drei Möglichkeiten wie zwei Ebenen E und F im Raum zueinander liegen können:
- E und F sind identisch
- E und F liegen parallel zueinander
- E und F schneiden sich
Zur Untersuchung der Lagebeziehungen kann man die Ebenengleichungen der beiden Ebenen miteinander gleichsetzen. Mit der Lösung des daraus entstehenden LGS kann man dann Aussagen über die Lagebeziehung treffen:
Aufgabe: Ergebnisse interpretieren
Interpretiere die jeweilige Situation geometrisch.
a) 
b) 
c) 
Aufgabe: Lagebeziehungen berechnen
Untersuche die Lagebeziehung der jeweiligen Ebenen.
a) 
b) 
c) 
Aufgabe: Schnitt von zwei Zeltflächen
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen  und
und  . Berechne die Geradengleichung der oberen Zeltkante.
. Berechne die Geradengleichung der oberen Zeltkante.
⭐Berechnung des Winkels zwischen Ebene und Ebene
Merke: Winkel berechnen zwischen zwei Ebenen
Inhalt
Beispiel: Winkel berechnen zwischen zwei Ebenen
Inhalt
Aufgabe <Nummer>: Fehlerbeschreibung
Inhalt
Aufgabe <Nummer>: Zeltwände
Inhalt

 Die Gerade g und die Ebene E schneiden sich.
Die Gerade g und die Ebene E schneiden sich.