|
|
| Zeile 38: |
Zeile 38: |
|
| |
|
| * E und F sind identisch | | * E und F sind identisch |
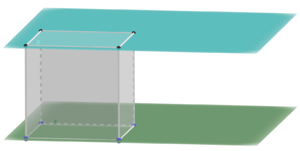
| * E und F liegen parallel zueinander | | * E und F liegen parallel zueinander [[Datei:Parallele Ebenen.png|ohne|rahmenlos]] |
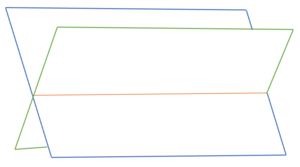
| * E und F schneiden sich [[Datei:Schnittgerade zweier Ebenen.png|ohne|rahmenlos]] | | * E und F schneiden sich [[Datei:Schnittgerade von zwei Ebenen.png|ohne|rahmenlos]] |
|
| |
|
| Zur Untersuchung der Lagebeziehungen kann man die Ebenengleichungen der beiden Ebenen miteinander gleichsetzen. Mit der Lösung des daraus entstehenden LGS kann man dann Aussagen über die Lagebeziehung treffen: | | Zur Untersuchung der Lagebeziehungen kann man die Ebenengleichungen der beiden Ebenen miteinander gleichsetzen. Mit der Lösung des daraus entstehenden LGS kann man dann Aussagen über die Lagebeziehung treffen: |
Version vom 25. April 2021, 15:03 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Für die Lage einer Gerade g zu einer Ebene E sind 3 Fälle möglich:
- Die Gerade g liegt in der Ebene E.
- Die Gerade g liegt parallel zur Ebene E.
- Die Gerade g und die Ebene E schneiden sich.
Untersuchung der Lagebeziehung
Vorgehen
Beispiel (Ebene in Parameterform)
Übungsaufgaben (Learning App)
Beispiel (Ebene in Koordinatenform)
Übungsaufgaben
Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Basiswissen
Lagebeziehung zwischen Ebenen
Es gibt drei Möglichkeiten wie zwei Ebenen E und F im Raum zueinander liegen können:
- E und F sind identisch
- E und F liegen parallel zueinander
- E und F schneiden sich
Zur Untersuchung der Lagebeziehungen kann man die Ebenengleichungen der beiden Ebenen miteinander gleichsetzen. Mit der Lösung des daraus entstehenden LGS kann man dann Aussagen über die Lagebeziehung treffen:
Aufgabe: Ergebnisse interpretieren
Interpretiere die jeweilige Situation geometrisch.
a) 
b) 
c) 
Aufgabe: Lagebeziehungen berechnen
Untersuche die Lagebeziehung der jeweiligen Ebenen.
a) 
b) 
c) 
Aufgabe: Schnitt von zwei Zeltflächen
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen  und
und  . Berechne die Geradengleichung der oberen Zeltkante.
. Berechne die Geradengleichung der oberen Zeltkante.