Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 17: | Zeile 17: | ||
{{Box|1=Definition | {{Box|1=Definition | ||
|2=Jede Gerade lässt sich durch eine Gleichung der Form <math>g: \vec{x} = \vec{OA} + k \cdot \vec{v}, r \in \mathbb{R}</math> beschreiben. | |2=Jede Gerade lässt sich durch eine Gleichung der Form <math>g: \vec{x} = \vec{OA} + k \cdot \vec{v}, r \in \mathbb{R}</math> beschreiben. | ||
* <math> | * Diese Vektorgleichung bezeichnet man als '''Parameterdarstellung''' oder '''Parametergleichung''' der Geraden <math>g</math> mit dem '''Parameter''' <math>k</math>. | ||
* Setzt man für <math>k</math> irgendeine Zahl in die Parameterdarstellung der Geraden <math>g</math> ein, so ergibt sich der Ortsvektor <math>\vec{x}</math> (auch <math>\vec{OX}</math> genannt) eines Punktes <math>X</math> der Geraden <math>g</math>. | |||
* Der Vektor <math>\vec{OA}</math> heißt '''Stützvektor'''. Er ist der Ortsvektor zu einem Punkt <math>A</math> (auch Aufpunkt genannt), der auf der Geraden <math>g</math> liegt. | * Der Vektor <math>\vec{OA}</math> heißt '''Stützvektor'''. Er ist der Ortsvektor zu einem Punkt <math>A</math> (auch Aufpunkt genannt), der auf der Geraden <math>g</math> liegt. | ||
* Der Vektor <math>\vec{v} \neq \vec{o}</math> heißt '''Richtungsvekor'''. | * Der Vektor <math>\vec{v} \neq \vec{o}</math> heißt '''Richtungsvekor'''. | ||
|3=Merksatz}} | |3=Merksatz}} | ||
Version vom 25. April 2021, 14:57 Uhr
Geraden und ihre Darstellungsformen
Parameterdarstellung einer Geraden
Wie du nun eine Parametergleichung durch zwei gegebene Punkte aufstellst, wird im folgenden Video erklärt:
????Anmerkung zu den Lösungen: Wie du wahrscheinlich im obigen Video mitbekommen hast, gibt es unendlich viele Lösungen. Daher sind auch Vielfache der Richtungsvektoren oder andere Stützvektoren, wenn sie auf der Geraden liegen, möglich.????
Du kannst aber auch eine Gerade aufstellen, die durch einen Punkt verläuft und parallel zu einer anderen Gerade oder zu einer der Koordinatenachsen ist.
Hier noch eine Aufgabe zu Geraden mit besonderen Lagen im Koordinatensystem:
Punktprobe
Wie du überprüfst, ob ein gegebener Punkt auf einer gegebenen Gerade der daneben liegt, erfährst du im folgenden Video:
Spurpunkte einer Geraden
Strecken
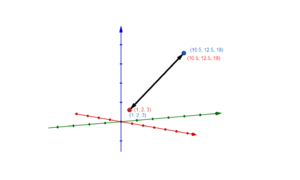
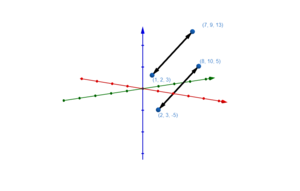
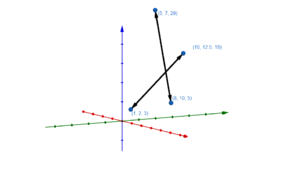
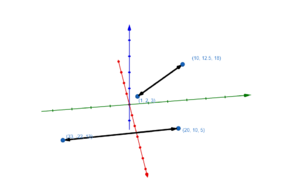
Graphische Darstellung von Geraden im Raum
Lagebeziehungen von Geraden