Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 76: | Zeile 76: | ||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 3: Lage erkennen|2=Löse das Quiz und mache dir deinen eigenen Lernzettel | ||
<iframe src="https://learningapps.org/watch?app=19038875" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?app=19038875" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 100: | Zeile 100: | ||
|3= Merksatz}} | |3= Merksatz}} | ||
{{Box|1= Aufgabe | {{Box|1= Aufgabe 4: |2=Flugerlaubnis erteilen? | ||
Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen zwei Flugzeuge starten. Hierzu gehört das Flugzeug der Fluglinie Aer. Es startet bei <math> \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}</math> und befindet sich nach 5sek auf <math> \begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix}</math>. Ebenfalls möchte das Flugzeug der Fluglinie Amadeus in die Luft. Dies startet in <math> \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix}</math>. Pro Sekunde legt es eine Strecke von 175,49m zurück und besitzt einen Richtungsvektor von <math> \begin{pmatrix} 120,2 \\ 96,4 \\ z \end{pmatrix}</math>. | Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen zwei Flugzeuge starten. Hierzu gehört das Flugzeug der Fluglinie Aer. Es startet bei <math> \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}</math> und befindet sich nach 5sek auf <math> \begin{pmatrix} 510 \\ 410 \\ 350 \end{pmatrix}</math>. Ebenfalls möchte das Flugzeug der Fluglinie Amadeus in die Luft. Dies startet in <math> \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix}</math>. Pro Sekunde legt es eine Strecke von 175,49m zurück und besitzt einen Richtungsvektor von <math> \begin{pmatrix} 120,2 \\ 96,4 \\ z \end{pmatrix}</math>. | ||
| Zeile 208: | Zeile 208: | ||
{{Box|1= Aufgabe | |||
{{Box|1= Aufgabe 5: |2=Ordne die Paare zu. | |||
<iframe src="https://learningapps.org/watch?app=18639143" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?app=18639143" style="border:0px;width:100%;height:500px" allowfullscreen="true" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
|Farbe={{Farbe|orange}}|3= Hervorhebung1}} | |Farbe={{Farbe|orange}}|3= Hervorhebung1}} | ||
Version vom 20. April 2021, 15:34 Uhr
Einführung
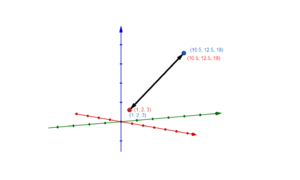
Parameterdarstellung einer Geraden
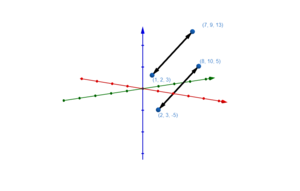
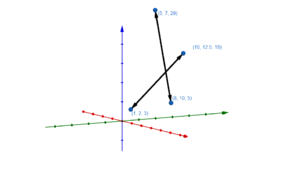
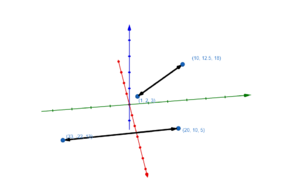
Lagebeziehungen von Geraden