Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum

Info

In diesem Lernpfadkapitel beschäftigst du dich mit Geraden im Raum. Du lernst, Geraden im Raum durch Vektoren zu beschreiben, Parameterdarstellungen und Spurpunkte von Geraden zu bestimmen, die Lage von Geraden im Raum und zueinander zu bestimmen sowie Geradenscharen zu bestimmen.

Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit
• und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Wir wünschen dir viel Erfolg!

Einführung

Parameterdarstellung einer Geraden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Aufgabe 1

Stelle eine Gleichung einer Geraden in Parameterdarstellung auf, die durch folgende Punkte verläuft: A(1/2/3), B(1/3/4)

Lagebeziehungen von Geraden

Hinweis

In diesem Abschnitt beschäftigst du dich mit der Lagebeziehung von Geraden im Raum.

Definition

Wir unterscheiden die Lage zweier Geraden in identisch, parallel, geschnitten und windschief. Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander kollinear (sind Vielfache voneinander), so können die Geraden lediglich identisch oder parallel sein.

Um nun zu untersuchen, ob die Geraden parallel oder identisch sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden identisch. Andernfalls sind die Geraden echt parallel.

Aufgabe 1: Lage erkennen

Wie verlaufen die folgenden Geraden zueinander?

a)$f_1: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $f_2: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, r \in \mathbb{R}$

b)$g_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $g_2: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

c)$i_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $i_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die erste Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren mit $\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 2 \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}$ ein Vielfaches voneinander (=kollinear) sind. Da beide Ortsvektoren identisch sind, liegt ein Punkt sind die Geraden identisch.

Die zweite Antwort lautet parallel. Die beiden Geraden sind parallel. Während die beiden Richtungsvektoren kollinear, sogar identisch, sind liegt der Ortsvektor von $i_2$ nicht auf der Geraden von$i_1: \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$, mit $r=\begin{pmatrix} 1 \\ 0.5 \\ 0.333 \end{pmatrix}$.

Die dritte Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren identisch sind ($\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$) und der Ortsvektor der einen Gerade auf der anderen Gerade ist: $\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$.

Definition

Sind die Richtungsvektoren nicht kollinear, so können die Geraden sich lediglich schneiden oder windschief zueinander sein.

Um nun zu untersuchen, ob sich die Geraden schneiden oder zueinader winschief sind, müssen wir schauen, ob sich ein Schnittpunkt berechnen lässt. Hierzu setzen wir die Geradengleichungen gleich und formen um. Erhalten wir einen Schnittpunkt S, so schneiden sich die Geraden im Punkt S. Andernfalls sind diese Geraden windschief zueinander.

Aufgabe 2: Lage erkennen

Wie verlaufen die folgenden Geraden zueinander?

a)$g_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $g_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

b)$h_1: \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 4 \\ 4 \end{pmatrix}, r \in \mathbb{R}$ und $h_2: \vec{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \cdot \begin{pmatrix} 4 \\ 5 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

c)$i_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R}$ und $i_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}, r \in \mathbb{R}$

Die erste Antwort lautet schneiden. Die beiden Geraden schneiden sich im Punkt .

Die zweite Antwort lautet schneiden. Die beiden Geradenschneiden sich.

Die dritte Antwort lautet windschief. Die beiden Geraden sind windschief zueinander. Dies sehen wir daran,

Aufgabe 1: Lage erkennen

Löse das Quiz und mache dir deinen eigenen Lernzettel

Merksatz

Zwei Geraden...

sind identisch

• Richtungsvektoren kollinear (= Vielfache voneinander)
• Ortsvektor der einen Geraden liegt auf der anderen Geraden

sind parallel

• Richtungsvektoren kollinear (= Vielfache voneinander)
• Ortsvektor der einen Geraden liegt nicht auf der anderen Geraden.

schneiden sich

• Richtungsvektoren nicht kollinear (= Vielfache voneinander)
• Bei dem Versuch einen Schnittpunkt zu berechnen, kommt eine wahre Aussage in Form eines Punktes heraus

sind zueinander windschief

• Richtungsvektoren nicht kollinear (= Vielfache voneinander)
• Bei dem Versuch einen Schnittpunkt zu berechnen, kommt eine falsche Aussage heraus

.

Aufgabe 3:

Flugerlaubnis erteilen?

Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen zwei Flugzeuge starten. Hierzu gehört das Flugzeug der Fluglinie Aer. Es startet bei $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix}$ und befindet sich nach 10sek auf $\begin{pmatrix} 1239,75 \\ 1040 \\ 1287,5 \end{pmatrix}$. Ebenfalls möchte das Flugzeug der Fluglinie Amadeus in die Luft. Dies startet in $\begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix}$. Pro Sekunde legt es eine Strecke von 164,85m zurück und besitzt einen Richtungsvektor von $\begin{pmatrix} 98,88 \\ 82,4 \\ z \end{pmatrix}$.

Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher. Hilf ihm die Antworten auf folgende Fragen zu finden:

a) Wie lauten die Geradengleichungen der einzelen Flugzeuge?

b) Wie schnell (in km/h) fliegen die einzelnen Flugzeuge?

c) Können alle Flugzeuge starten, ohne dass es zu einer Kollision kommt?

Zu Aer: Setze alle gegebenen Daten in eine allgemeine Parameterdarstellung ein und forme um.

Zu Amadeus: Um den Richtungsvektor zu berechnen, benötigst du die Forme zur Berechnung der Länge eines Vektoren: $L=\sqrt[2]{x{2}+y^{2}+z^{2}}$.

L=

Geschwindigkeit kann man in verschiedene Einheiten angeben, z.B.: km/h, m/s etc.. Nachdem du die Länge der Strecke nach einer Sekunde berechnet hast, musst du dies von m/s zu km/h umwandeln.

Nur weil sich zwei Geraden schneiden heißt es noch nicht direkt, dass eine Kollision vorherrscht.

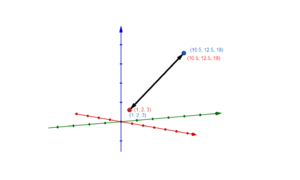
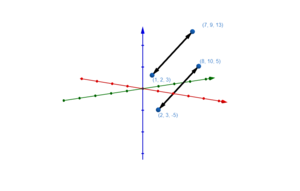
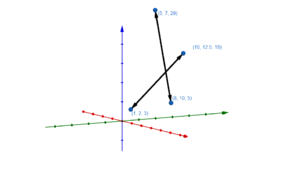
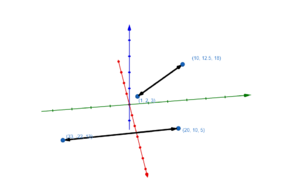
Flugzeug Aer: $f_3: \vec{x} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 122,975 \\ 103 \\ 128,75 \end{pmatrix}, t \in \mathbb{R}$

Dies erhalten wir, indem wir folgendes berechnen: $\begin{pmatrix} 1239,75 \\ 1040 \\ 1287,5 \end{pmatrix} = \begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 10 \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix}, t \in \mathbb{R}$. Dies schreiben wir in ein Gleichugssystem um und formen es zu x,y,z um:

$1239,75=10+10*x$

$1040 =10+10*y$

$1287,5 = 0+10*z$

Flugzeug Amadeus: $f_1: \vec{x} = \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 98,88\\ 82,4 \\ 103\end{pmatrix}, t \in \mathbb{R}$

Dies erhalten wir wie folgt: Wir kennen den Richtungsvektor: $\begin{pmatrix} 98,88 \\ 82,4 \\ z \end{pmatrix}$. Nun müssen wir z berechnen. Im Text steht, dass das Flugzeug pro Sekunde eine Länge von 164,85m fliegt. Das bedeutet, dass der Richtungsvektor eine Länge von 164,85 beträgt. Dies können wir mit der Formel der Länge eines Vektor berechnen:

$164,85=\sqrt[2]{98,88^{2}+82,4^{2}+z^{2}}$

Indem wir beide Seiten zum Quadart nehemn, entfällt die Wurzel und es folgt:

$164,85^{2}=98,88^{2}+82,4^{2}+z^{2}$

Wir formen zu $z^{2}$ um und ziehen dann die Wurzel. Wir erhalten 102,997 und runden auf 103.

Wobei t für die Zeit in Sekunden steht.

Wir berechnen die Geschwindigkeit, indem wir die Länge des Richtungsvektors berechnen. Dies erfolgt it der Formel: $f_2: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 96\\ 80 \\ 100 \end{pmatrix}, t \in \mathbb{R}$ Flugzeug Amadeus:

Das Flugzeug Liesbeth hat nach dem Text eine Geschwindigkeit von 160 m/s

Flugzeug Aer und Amadeus: Sie schneiden sich für $\begin{pmatrix} 10 \\ 10 \\ 0 \end{pmatrix} + 8 \cdot \begin{pmatrix} 122,975 \\ 103 \\ 128,75 \end{pmatrix}= \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} + 10 \cdot \begin{pmatrix} 98,88\\ 82,4 \\ 103\end{pmatrix}$. Dies erhalten wir, indem wir beide Funktionen gleichsetzen.

Da es jedoch nicht der gleiche Zeitpunkt ist, kommt es zu keiner Kollision.