Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 36: | Zeile 36: | ||
{{Box|1= Aufgabe 1: Lage erkennen|2= | {{Box|1= Aufgabe 1: Lage erkennen|2=Wie verlaufen die folgenden Geraden zueinander? | ||
<math>f_1: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>f_1: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, r \in \mathbb{R} </math> | <math>f_1: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>f_1: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}, r \in \mathbb{R} </math> | ||
<math>g_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>g_2: \vec{x} = \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> | |||
<math> | <math>i_1: \vec{x} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> und <math>i_2: \vec{x} = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, r \in \mathbb{R} </math> | ||
{{Lösung versteckt|1= Die erste Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren ein Vielfaches voneinander (=kollinear) sind ( <math> \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 2 \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix} </math>) und beide Ortsvektoren identisch sind.|2=Lösung Aufgabe a |3=Lösung Aufagbe a}} | |||
{{Lösung versteckt|1= Die zweite Antwort lautet parallel. Während die beiden Richtungsvektoren kollinear, sogar identisch sind, liegt der Ortsvektor von i_2 nicht auf der Geraden <math> i_1: \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>, mit <math>r=\begin{pmatrix} 1 \\ 0.5 \\ 0.333 \end{pmatrix}</math>.|2=Lösung Aufgabe b|3=Lösung Aufgabe b}} | |||
{{Lösung versteckt|1= Die dritte Antwort lautet identisch. Die beiden Geraden sind identisch. Dies sehen wir daran, dass die Richtungsvekoren identisch sind (<math>\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>) und der Ortsvektor der einen Gerade auf der anderen Gerade ist: <math>\begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix}= \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + 1 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}</math>. |2=Lösung Aufgabe c|3=Lösung Aufgabe c}} | |||
|Farbe={{Farbe|orange}}|3= Hervorhebung1}} | |||
{{Box|1=Definition | {{Box|1=Definition | ||
Version vom 17. April 2021, 12:28 Uhr
Einführung
Parameterdarstellung einer Geraden
Lagebeziehungen von Geraden
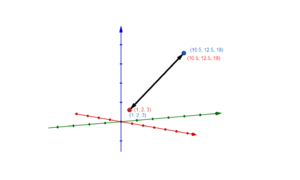
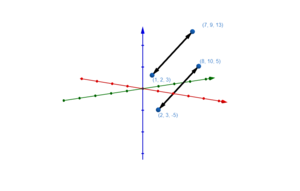
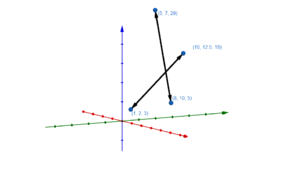
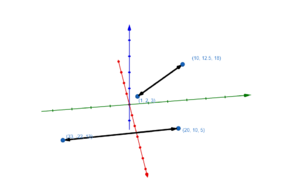
Im Folgenden wollen wir betrachten, wie verschiedene Geraden zueinander im Raum liegen.
Aufgaben geschnitten oder windschief