Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 15: | Zeile 15: | ||
Berechne dann mithilfe von Sinus, Kosinus und Tagens die fehlenden Strecken in den rechtwinkligen Teildreiecken.<br> | Berechne dann mithilfe von Sinus, Kosinus und Tagens die fehlenden Strecken in den rechtwinkligen Teildreiecken.<br> | ||
Übertrage die Beispiele in dein Heft (Skizze und Rechnungen)|Arbeitsmethode}} | Übertrage die Beispiele in dein Heft (Skizze und Rechnungen)|Arbeitsmethode}} | ||
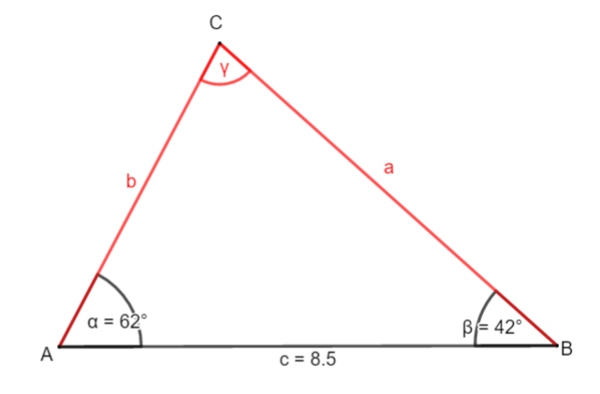
=== 3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben=== | ===3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben=== | ||
<br> | <br> | ||
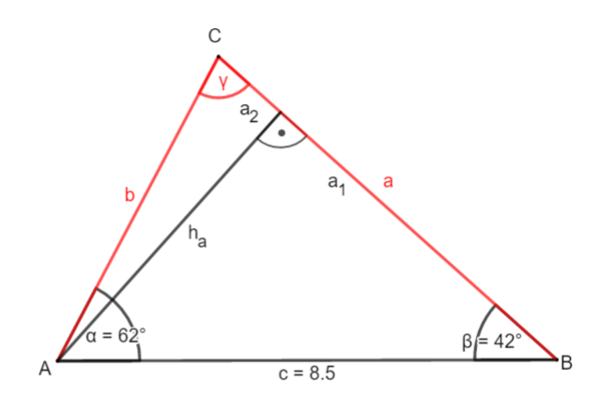
'''1. Möglichkeit:''' Zerlege das Dreieck durch die '''Höhe h<sub>a</sub>''' ein zwei rechtwinklige Dreiecke.<br> | |||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">[[Datei:Dreieck 1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|600x600px]]</div> | <div class="width-1-2">[[Datei:Dreieck 1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|600x600px]]</div> | ||
| Zeile 22: | Zeile 23: | ||
</div> | </div> | ||
<br> | <br> | ||
① Bestimme γ:<br> | ① Bestimme γ:<br> | ||
Winkelsummensatz<br> | Winkelsummensatz<br> | ||
| Zeile 62: | Zeile 63: | ||
</div> | </div> | ||
<br> | <br> | ||
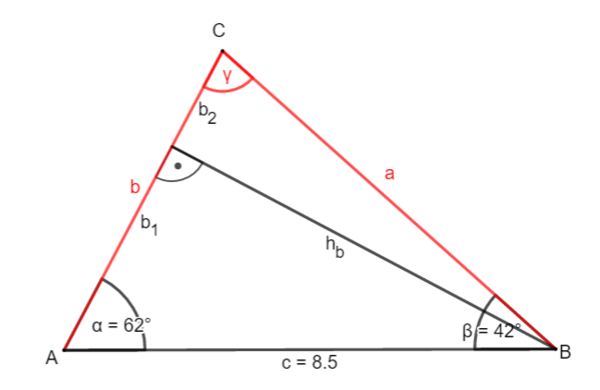
'''2. Möglichkeit:''' Zerlege das Dreieck durch die '''Höhe h<sub>b</sub>''' ein zwei rechtwinklige Dreiecke.<br> | |||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">[[Datei:Dreieck 1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|600x600px]]</div> | <div class="width-1-2">[[Datei:Dreieck 1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|600x600px]]</div> | ||
| Zeile 68: | Zeile 69: | ||
</div> | </div> | ||
<br> | <br> | ||
① Bestimme γ:<br> | ① Bestimme γ:<br> | ||
Winkelsummensatz<br> | Winkelsummensatz<br> | ||
| Zeile 106: | Zeile 106: | ||
</div> | </div> | ||
<br> | <br> | ||
=== 3.2 Beispiel 2: Zwei Seiten und ein Winkel sind gegeben === | ===3.2 Beispiel 2: Zwei Seiten und ein Winkel sind gegeben=== | ||
<br> | <br> | ||
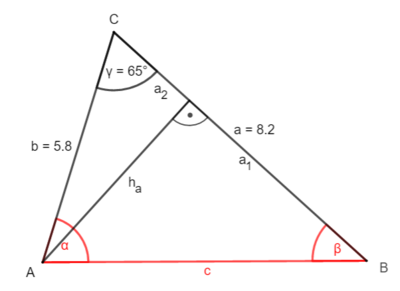
'''1. Möglichkeit:''' Zerlege das Dreieck durch die '''Höhe h<sub>a</sub>''' ein zwei rechtwinklige Dreiecke.<br> | |||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">[[Datei:Dreieck 3 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | <div class="width-1-2">[[Datei:Dreieck 3 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | ||
<div class="width-1-2">[[Datei:Dreieck 3.1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | <div class="width-1-2">[[Datei:Dreieck 3.1 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | ||
</div> | </div> | ||
① Bestimme h<sub>a</sub>:<br> | ① Bestimme h<sub>a</sub>:<br> | ||
sin γ = <math>\tfrac{h_a}{b}</math> |·b<br> | sin γ = <math>\tfrac{h_a}{b}</math> |·b<br> | ||
| Zeile 163: | Zeile 164: | ||
<div class="width-1-2">[[Datei:Dreieck 3.2 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | <div class="width-1-2">[[Datei:Dreieck 3.2 Einstieg Berechnungen in allgemeinen Dreiecken.png|rahmenlos|400x400px]]</div> | ||
</div> | </div> | ||
<br> | |||
① Bestimme h<sub>b</sub>:<br> | ① Bestimme h<sub>b</sub>:<br> | ||
sin γ = <math>\tfrac{h_b}{a}</math> |·a<br> | sin γ = <math>\tfrac{h_b}{a}</math> |·a<br> | ||
Version vom 8. März 2021, 14:56 Uhr
SEITE IM AUFBAU
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken
Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.
Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.
3.1 Beispiel 1: Eine Seite und zwei Winkel sind gegeben
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne ha:
sin β = | ·c
c · sin β = ha
8,5 · sin(42°) = ha
5,7 (cm) ha
③ Berechne b:
sin γ = | ·b
b · sin γ = ha | : sin γ
b =
b =
b 5,9 (cm)
④ Berechne a:
cos β = | ·c
c · cos β = a1
8,5 · cos (42°) = a1
cos γ = | ·c
b · cos γ = a2
5,9 · cos (76°) = a2
= 6,3 + 1,4
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
② Berechne hb:
sin α = | ·c
c · sin α = hb
8,5 · sin(62°) = hb
7,5 (cm) hb
③ Berechne a:
sin γ = | ·a
a · sin γ = hb | : sin γ
a =
a =
a 7,7 (cm)
④ Berechne b:
cos α = | ·c
c · cos α = b1
8,5 · cos (62°) = b1
cos γ = | ·c
a · cos γ = b2
7,7 · cos (76°) = b2
= 4,0 + 1,9
3.2 Beispiel 2: Zwei Seiten und ein Winkel sind gegeben
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
① Bestimme ha:
sin γ = |·b
b · sin γ = ha
5,8 · sin(65°) = ha
5,2 (cm) ha
② Bestimme a2
cos γ = |·b
b · cos γ = a2
5,8 · cos(65°) = a2
2,5 (cm) a2
③ Bestimme a1
a – a2= a1
8,2 - 3,8 = a1
5,7 (cm) = a1
④ Bestimme β
tan β =
tan β = |tan-1
β 42,4°
⑤ Bestimme c
sin β = |·c
c · sin β = ha |: sin β
c =
c =
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel α
Winkelsumme
α + β + γ = 180° |- β; -γ
α = 180° - β - γ
α = 180° - 42,4° - 65°
α = 72,6°
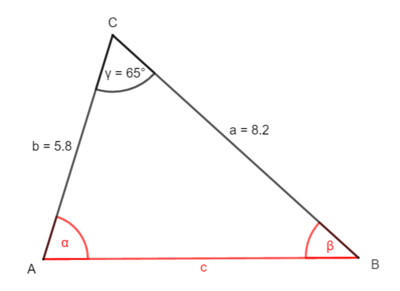
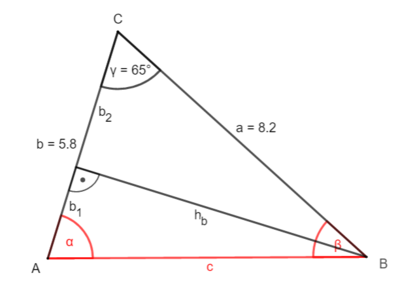
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
① Bestimme hb:
sin γ = |·a
a · sin γ = hb
8,2 · sin(65°) = hb
7,4 (cm) hb
② Bestimme b2
cos γ = |·a
a · cos γ = b2
8,2 · cos(65°) = b2
3,5 (cm) b2
③ Bestimme b1
b – b2= b1
5,8 - 3,5 = b1
2,3 (cm) = b1
④ Bestimme α
tan α =
tan α = |tan-1
α 72,7°
⑤ Bestimme c
sin α = |·c
c · sin α = hb |: sin α
c =
c =
c=
c =
c 7,7 (cm)
⑥ Bestimme den letzten Winkel β
Winkelsumme
α + β + γ = 180° |- α; -γ
β = 180° - α - γ
β= 180° - 72,7° - 65°
β = 42,3°
Du merkst, es kommt zu Rundungsungenauigkeiten.