Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken

SEITE IM AUFBAU

zurück zur Seite der Herta-Lebenstein-Realschule

Startseite (Vorwissen)

1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken

3) Berechnungen in allgemeinen Dreiecken

3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken

Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.

Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.

Strecken- und Winkelberechnungen in allgemeinen Dreiecken

Zerlege das allgemeine Dreieck in zwei rechtwinklige Dreiecke. Zeichne dazu eine geeignete Höhe h ein.
Berechne dann mithilfe von Sinus, Kosinus und Tagens die fehlenden Strecken in den rechtwinkligen Teildreiecken.

Übertrage die Beispiele in dein Heft (Skizze und Rechnungen)

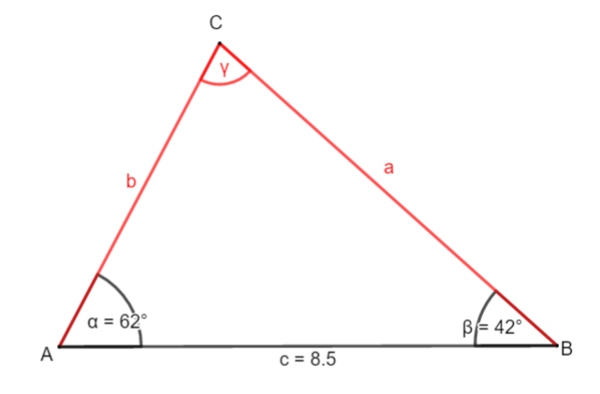
Beispiel 1: Eine Seite und zwei Winkel sind gegeben

① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
&nbps;  = 180° - 42° - 62°
   = 76°

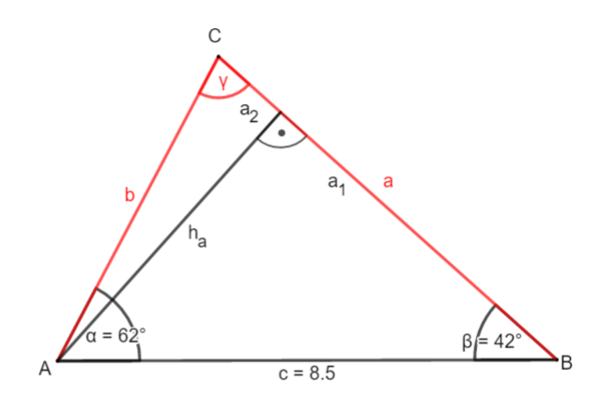
② Berechne h_a:
sin β = $\tfrac{h_a}{c}$   | ·c
c · sin β = h_a
8,5 · sin(42°) = h_a
5,7 (cm)$\approx$ h_a

③ Berechne b:
sin γ = $\tfrac{h_a}{b}$   | ·b
b · sin γ = h_a   | : sin γ
b = $\tfrac{h_a}{sin\gamma}$
b = $\tfrac{5,7}{sin(76°)}$
b $\approx$ 5,9 (cm)

④ Berechne a₁:

Übung 1 (online und im Heft)

Löse auf der Seite Aufgabenfuchs die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft.

• 61
• 62
• 63