Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 733: | Zeile 733: | ||
{{Lösung versteckt|1='''a)''' Insgesamt gibt es <math>13</math> Spielsteine. Aufgrund der übereinstimmenden Größe und Beschaffenheit der Steine, ist die Wahrscheinlichkeit für jeden einzelnen Spielstein gleich und beträgt <math>\tfrac{1}{13}</math>. Aus diesem Grund handelt es sich bei dieser Aufgabe um ein Laplace Experiment. | {{Lösung versteckt|1='''a)''' Insgesamt gibt es <math>13</math> Spielsteine. Aufgrund der übereinstimmenden Größe und Beschaffenheit der Steine, ist die Wahrscheinlichkeit für jeden einzelnen Spielstein gleich und beträgt <math>\tfrac{1}{13}</math>. Aus diesem Grund handelt es sich bei dieser Aufgabe um ein Laplace Experiment. | ||
Da unter den Steinen nur einmal der Buchstabe D vorhanden ist gilt: P("D wird gezogen") = <math>\tfrac{1}{13}</math>. |2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' Es gibt zwei Spielsteine mit dem Buchstaben N, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. | |||
{{Lösung versteckt|1='''b)''' | |||
Es gibt zwei Spielsteine mit dem Buchstaben N, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. | |||
Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der beiden möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der beiden möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | ||
Es gilt also: P( | Es gilt also: P("N wird gezogen") = <math>\tfrac{1}{13}</math> + <math>\tfrac{1}{13}</math> = <math>\tfrac{2}{13}</math>|2=Lösung b)|3=Lösung}} | ||
{{Lösung versteckt|1='''c)''' Es gibt insgesamt <math>3</math> Spielsteine mit dem Buchstaben O, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der drei möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | |||
{{ | Es gilt also: P("O wird gezogen") = <math>\tfrac{1}{13}</math> + <math>\tfrac{1}{13}</math> + <math>\tfrac{1}{13}</math> = <math>\tfrac{3}{13}</math>|2=Lösung c) |3=Lösung}} | ||
Insgesamt gibt es einen Spielstein mit A und drei mit einem O. Die restlichen Vokale sind nicht vorhanden. | {{Lösung versteckt|1='''d)''' Insgesamt gibt es einen Spielstein mit A und drei mit einem O. Die restlichen Vokale sind nicht vorhanden. | ||
Somit folgt mit der Summenregel: P( | Somit folgt mit der Summenregel: P("Vokal wird gezogen") = <math>\tfrac{1}{13}</math> + <math>\tfrac{3}{13}</math> = <math>\tfrac{4}{13}</math>|2=Lösung d)|3=Lösung}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
Version vom 29. November 2020, 12:11 Uhr
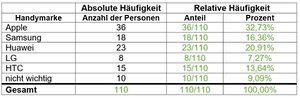
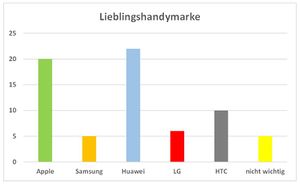
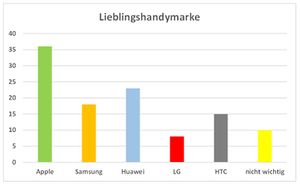
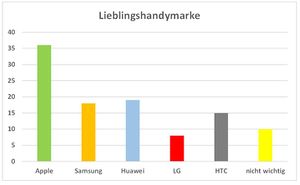
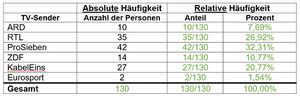
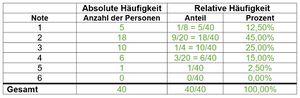
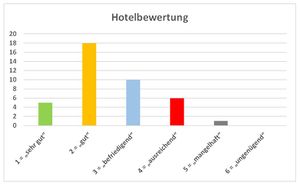
Absolute und relative Häufigkeit
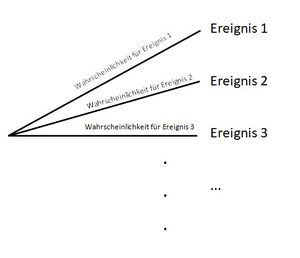
Zufallsexperimente
Laplace-Experimente