Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 3: | Zeile 3: | ||
|2= | |2= | ||
In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. Es gibt | In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. Es gibt drei Themengebiete, auf die du über das Inhaltsverzeichnis zugreifen kannst. | ||
Zum Lösen der Aufgaben benötigst du Stift, Papier und deinen Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen genau. | Zum Lösen der Aufgaben benötigst du Stift, Papier und deinen Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen genau. | ||
| Zeile 440: | Zeile 440: | ||
{{Box | Beispiel: Zufallsexperimente | | {{Box | Beispiel: Zufallsexperimente | | ||
Berechnet man die Wahrscheinlichkeit davon, dass beim Drehen dieses Glücksrad auf "rot" stehen bleibt, so betrachtet man den Anteil der roten Fläche an der gesamten Fläche des Glückrades. | Berechnet man die Wahrscheinlichkeit davon, dass beim Drehen dieses Glücksrad auf "rot" stehen bleibt, so betrachtet man den Anteil der roten Fläche an der gesamten Fläche des Glückrades. | ||
Diese beträgt 75%. Das heißt, die Wahrschienlichkeit, dass das Glücksrad auf rot stehen bleibt, liegt bei 75% oder <math>\tfrac{3}{4}</math>. | Beispiel}} | Diese beträgt <math>75 %</math>. Das heißt, die Wahrschienlichkeit, dass das Glücksrad auf rot stehen bleibt, liegt bei <math>75 %</math> oder <math>\tfrac{3}{4}</math>. | Beispiel}} | ||
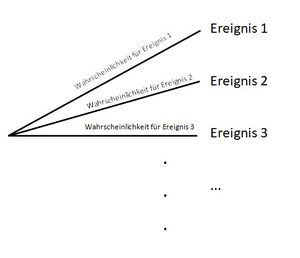
{{Box | Baumdiagramme| | {{Box | Baumdiagramme| | ||
| Zeile 453: | Zeile 453: | ||
'''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | '''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | ||
Wenn du hier die Wahrscheinlichkeit in Prozent berechnest, | Wenn du hier die Wahrscheinlichkeit in Prozent berechnest, gib die Prozentzahl mit zwei Nachkommastellen an. | ||
{{Lösung versteckt|1= Zeichne ein Baumdiagramm. Was sind die Ereignisse? | {{Lösung versteckt|1= Zeichne ein Baumdiagramm. Was sind die Ereignisse? | ||
| Zeile 469: | Zeile 469: | ||
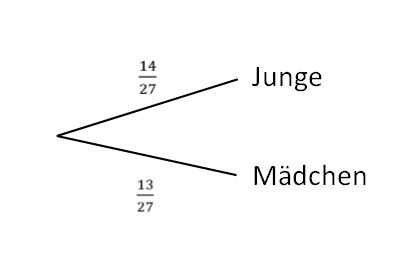
[[Datei:Baumdiagramm A1 a.jpg|zentriert]] | [[Datei:Baumdiagramm A1 a.jpg|zentriert]] | ||
Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr 51,85%. | Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr <math>51{,}85 %</math>. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
| Zeile 476: | Zeile 476: | ||
{{Lösung versteckt|1= Wie viele Personen stehen nun zur Auswahl? {{ Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}}|2=Tipps|3=Tipp}} | {{Lösung versteckt|1= Wie viele Personen stehen nun zur Auswahl? {{ Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}}|2=Tipps|3=Tipp}} | ||
{{Lösung versteckt|1= Wenn man ein Baumdiagramm zeichnet, so müssen | {{Lösung versteckt|1= Wenn man ein Baumdiagramm zeichnet, so müssen drei Ereignisse dargestellt werden: | ||
1. Ein Junge wird gelost. | 1. Ein Junge wird gelost. | ||
| Zeile 488: | Zeile 488: | ||
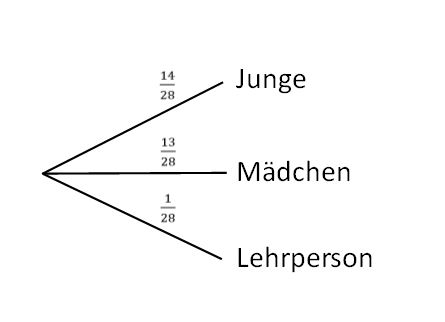
[[Datei:Baumdiagramm A1 b.jpg|zentriert]] | [[Datei:Baumdiagramm A1 b.jpg|zentriert]] | ||
Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei . | Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei <math>3{,}57 %</math>. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
| Zeile 494: | Zeile 494: | ||
{{Box | Komplementärregel| | {{Box | Komplementärregel| | ||
Hat ein Experiment genau zwei Ereignisse, so spricht man von Ereignis <math>E</math> und Gegenereignis <math>\bar E</math>. Die Wahrscheinlichkeiten der beiden ergeben in der Summe 1: | Hat ein Experiment genau zwei Ereignisse, so spricht man von Ereignis <math>E</math> und Gegenereignis <math>\bar E</math>. Die Wahrscheinlichkeiten der beiden ergeben in der Summe <math>1</math>: | ||
<math>P(E)+P(\bar E)=1</math>. | <math>P(E)+P(\bar E)=1</math>. | ||
| Zeile 505: | Zeile 505: | ||
[[Datei:Urne A2 1.jpg|mini|links|Abbildung 1]][[Datei:Plakat.jpg|mini|zentriert|Abbildung 2]] | [[Datei:Urne A2 1.jpg|mini|links|Abbildung 1]][[Datei:Plakat.jpg|mini|zentriert|Abbildung 2]] | ||
{{Lösung versteckt| 1= Es sind 20 blaue, 12 rote, 9 gelbe und 3 grüne Kugeln. |2=Hilfe, falls du die Farben nicht unterscheiden kannst.|3=Hilfe, falls du die Farben nicht unterscheiden kannst.}} | {{Lösung versteckt| 1= Es sind <math>20</math> blaue, <math>12</math> rote, <math>9</math> gelbe und <math>3</math> grüne Kugeln. |2=Hilfe, falls du die Farben nicht unterscheiden kannst.|3=Hilfe, falls du die Farben nicht unterscheiden kannst.}} | ||
Nun ziehst du ohne hinzuschauen eine Kugel. | Nun ziehst du ohne hinzuschauen eine Kugel. | ||
'''a)''' Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an. Runde das Ergebnis auf | '''a)''' Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an. Runde das Ergebnis auf zwei Nachkommastellen. | ||
{{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | {{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1= Hier kann man das Baumdiagramm auf | {{Lösung versteckt|1= Hier kann man das Baumdiagramm auf zwei Arten zeichnen. | ||
Man kann | Man kann ein Baumdiagramm mit vier Ereignissen zeichnen: | ||
1. Die Kugel ist grün. | 1. Die Kugel ist grün. | ||
| Zeile 529: | Zeile 529: | ||
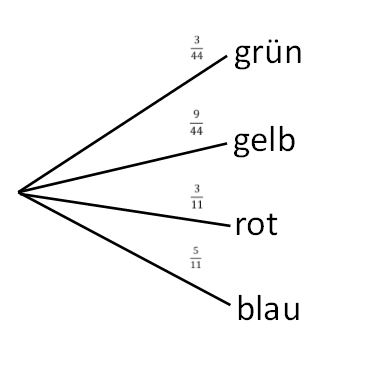
[[Datei:Baumdiagramm A2 a.jpg|zentriert]] | [[Datei:Baumdiagramm A2 a.jpg|zentriert]] | ||
Optional kann man man | Optional kann man man ein Baumdiagramm mit zwei Ereignissen zeichnen: | ||
1. Die Kugel ist gelb. | 1. Die Kugel ist gelb. | ||
| Zeile 542: | Zeile 542: | ||
Rechne das nun in Prozent um: | Rechne das nun in Prozent um: | ||
<math>\tfrac{9}{44} \approx 0,2045 = 20,45 %.</math> | <math>\tfrac{9}{44} \approx 0{,}2045 = 20{,}45 %.</math> | ||
Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei 20,45%. | Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei <math>20{,}45 %</math>. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
'''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Begründe. | '''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Begründe. | ||
{{Lösung versteckt| 1= Berechne zunächst die einzelnen Wahrscheinlichkeiten.Gibt die Lösung wieder in Prozent an. Runde das Ergebnis auf | {{Lösung versteckt| 1= Berechne zunächst die einzelnen Wahrscheinlichkeiten.Gibt die Lösung wieder in Prozent an. Runde das Ergebnis auf zwei Nachkommastellen. {{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}}|2=Tipp|3=Tipp}} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 557: | Zeile 557: | ||
</quiz> | </quiz> | ||
{{Lösung versteckt|1= Auch hier kann das Baumdiagramm auf | {{Lösung versteckt|1= Auch hier kann das Baumdiagramm auf zwei Arten gezeichnet werden: | ||
Man kann | Man kann ein Baumdiagramm mit vier Ereignissen zeichnen: | ||
1. Die Kugel ist grün. | 1. Die Kugel ist grün. | ||
| Zeile 573: | Zeile 573: | ||
[[Datei:Baumdiagramm A2 a.jpg|zentriert]] | [[Datei:Baumdiagramm A2 a.jpg|zentriert]] | ||
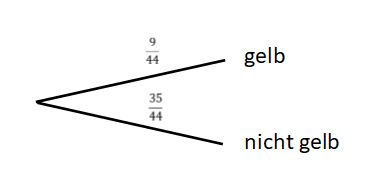
Optional kann eines mit | Optional kann eines mit zwei Ereignissen gezeichnet werden: | ||
Die Wahrscheinlichkeit für das Gewinnen ergibt sich aus der Komplementärregel. Die relative Häufigkeit der blauen Kugeln, mit denen man verliert, liegt bei <math>\tfrac{20}{44}=\tfrac{5}{11}</math>. Die Komplementärregel ergibt dann für das Gewinnen: <math>1-\tfrac{5}{11}=\tfrac{6}{11}</math>. | Die Wahrscheinlichkeit für das Gewinnen ergibt sich aus der Komplementärregel. Die relative Häufigkeit der blauen Kugeln, mit denen man verliert, liegt bei <math>\tfrac{20}{44}=\tfrac{5}{11}</math>. Die Komplementärregel ergibt dann für das Gewinnen: <math>1-\tfrac{5}{11}=\tfrac{6}{11}</math>. | ||
| Zeile 583: | Zeile 583: | ||
Nun rechnet man die Brüche in Prozent um: | Nun rechnet man die Brüche in Prozent um: | ||
Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0,4545 = 45,45 %</math>. | Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0{,}4545 = 45{,}45 %</math>. | ||
Wahrscheinlichkeit zu gewinnen: <math>100%-45,45%=54,55%</math>. | Wahrscheinlichkeit zu gewinnen: <math>100 %-45{,}45%=54{,}55%</math>. | ||
Die Wahrscheinlichkeit, zu gewinnen liegt bei 54,55 %, die zu verlieren bei 45,45%. Die Aussage stimmt also. | Die Wahrscheinlichkeit, zu gewinnen liegt bei <math>54{,}55 %</math>, die zu verlieren bei <math>45{,}45 %</math>. Die Aussage stimmt also. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
| Zeile 610: | Zeile 610: | ||
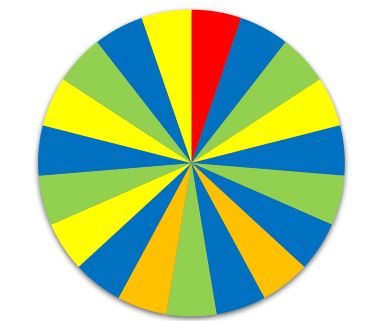
[[Datei:Glücksrad A3.jpg|zentriert]] | [[Datei:Glücksrad A3.jpg|zentriert]] | ||
{{Lösung versteckt| 1= Es gibt | {{Lösung versteckt| 1= Es gibt ein rotes Feld, zwei orangene, vier gelbe, fünf grüne und sieben blaue Felder. |2=Hilfe, falls du die Farben nicht unterscheiden kannst.|3=Hilfe, falls du die Farben nicht unterscheiden kannst.}} | ||
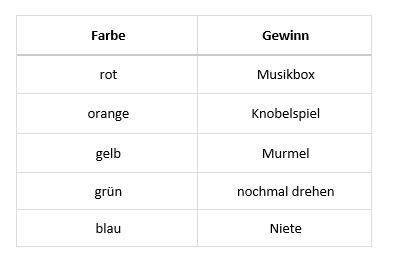
Man kann Folgendes gewinnen: | Man kann Folgendes gewinnen: | ||
| Zeile 643: | Zeile 643: | ||
</quiz> | </quiz> | ||
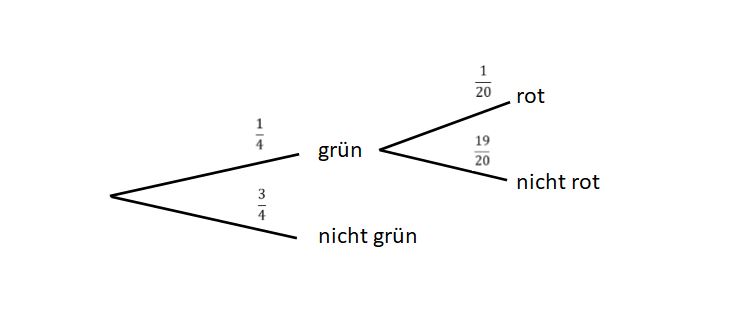
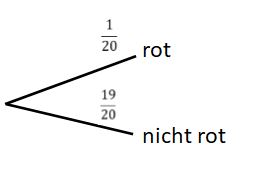
{{Lösung versteckt|1= Ein vereinfachtes Baumdiagramm hat | {{Lösung versteckt|1= Ein vereinfachtes Baumdiagramm hat zwei Ereignisse: | ||
1. Das Feld ist rot. | 1. Das Feld ist rot. | ||
Version vom 28. November 2020, 14:03 Uhr
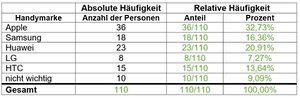
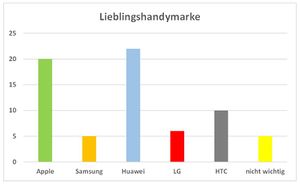
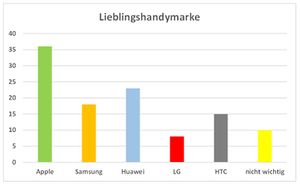
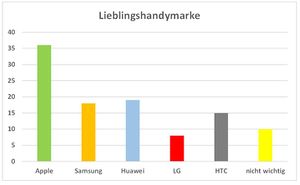
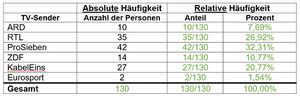
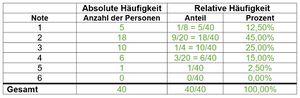
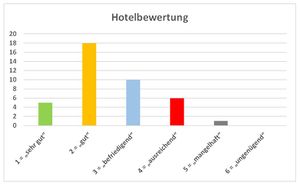
Absolute und relative Häufigkeit
Zufallsexperimente
Laplace-Experimente