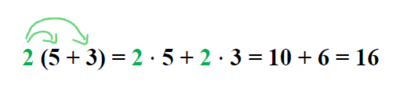Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 132: | Zeile 132: | ||
===2) Terme ausmultiplizieren und faktorisieren=== | ===2) Terme ausmultiplizieren und faktorisieren=== | ||
====Terme ausmultiplizieren==== | ====Terme ausmultiplizieren==== | ||
{{Box | 1= | {{Box | 1=Rechenregeln | 2=Das ''Ausmultiplizieren'' hat zum Ziel, eine Klammer aufzulösen. Um einen Faktor (im Bsp. 2) mit einer Klammer, in der eine Summe oder Differenz steht (im Bsp. 5 + 3), zu multiplizieren, '''muss der Faktor mit jedem Glied in der Klammer multipliziert werden''': <br /> | ||
[[Datei:Ausmultiplizieren 1.png|400px | links | thumb ]] <br /> <br /> <br /> <br /> <br /> <br /> | [[Datei:Ausmultiplizieren 1.png|400px | links | thumb ]] <br /> <br /> <br /> <br /> <br /> <br /> | ||
| Zeile 199: | Zeile 199: | ||
====Terme faktorisieren==== | ====Terme faktorisieren==== | ||
{{Box | 1= | {{Box | 1=Rechenregeln | 2=Beim ''Faktorisieren'' (auch genannt: ''Ausklammern'') geht es '''genau umgekehrt wie beim ''Ausmultiplizieren'' darum, etwas in einer Klammer zusammenzufassen.''' Wie das funktioniert, erklärt dir Lehrer Schmidt in folgendem Video: <br \> <br \> <div align="center">{{#ev:youtube|425_2PDl4b4}}</div> | ||
{{Lösung versteckt|1= <math> {\color{green}2}a+{\color{green}2}b = {\color{green}2}(a+b) </math> <br /> | {{Lösung versteckt|1= <math> {\color{green}2}a+{\color{green}2}b = {\color{green}2}(a+b) </math> <br /> | ||
<math> {\color{green}4}x+{\color{green}4}y = {\color{green}4}(x+y) </math> <br /> | <math> {\color{green}4}x+{\color{green}4}y = {\color{green}4}(x+y) </math> <br /> | ||
Version vom 22. November 2020, 17:04 Uhr
1) Terme zusammenfassen
Einführung
Wie kann ich Terme zusammenfassen?
Aufgabenteil
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Einführung
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgabenteil
| 1. binomische Formel | |||
| 2. binomische Formel | |||
| 3. binomische Formel | |||
| Das ist keine binomische Formel |
a)15()a()
b)3a()4b()3a()4b())
c)9u()2()
d)2m()7()
e)8y()10z()
f)6u()17w()6u()17w())