Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. Kurzbeschreibung des Aufbaus. | |2=In diesem Lernpfadkapitel kannst du deine Kenntnisse in der Stochastik verbessern und vertiefen. | ||
Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen. | |||
Kurzbeschreibung des Aufbaus. | |||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | * In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | ||
| Zeile 107: | Zeile 110: | ||
{{Lösung versteckt| 1= Die richtigen Zahlen für die absolute Häufigkeit findest du im Aufgabentext. |2= Tipp absolute Häufigkeit |3= }} | {{Lösung versteckt| 1= Die richtigen Zahlen für die absolute Häufigkeit findest du im Aufgabentext. |2= Tipp absolute Häufigkeit |3= }} | ||
{{Lösung versteckt| 1= Die richtigen Anteilswerte | {{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= Tipp Anteile |3= }} | ||
{{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Tipp Prozentzahlen |3= }} | {{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Tipp Prozentzahlen |3= }} | ||
| Zeile 243: | Zeile 246: | ||
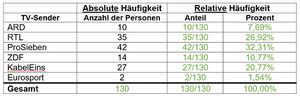
'''c)''' Gib die Anteile und Prozentwerte der relativen Häufigkeit für jeden TV-Sender an. Runde dabei auf 2 Nachkommastellen. | '''c)''' Gib die Anteile und Prozentwerte der relativen Häufigkeit für jeden TV-Sender an. Runde dabei auf 2 Nachkommastellen. | ||
{{Lösung versteckt| 1= Die richtigen Anteilswerte | {{Lösung versteckt| 1= Die richtigen Anteilswerte erhältst du, wenn du die Anzahl der Personen und die Gesamtzahl in einem Bruch aufschreibst. |2= Tipp Anteile |3= }} | ||
{{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Tipp Prozentzahlen |3= }} | {{Lösung versteckt| 1= Für die Berechnung der Prozentzahlen nutzt du deinen Taschenrechner und dividierst die berechneten Anteile durch die Gesamtzahl. |2= Tipp Prozentzahlen |3= }} | ||
| Zeile 425: | Zeile 428: | ||
==Zufallsexperimente== | ==Zufallsexperimente== | ||
{{Box | Zufallsexperimente | | {{Box | Zufallsexperimente | | ||
| Zeile 438: | Zeile 439: | ||
| Merksatz}} | | Merksatz}} | ||
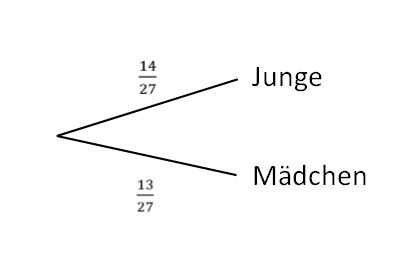
{{Box | Aufgabe | {{Box | Aufgabe 6: Klassendienste | In einer Klasse sind 14 Jungen und 13 Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost. | ||
'''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | '''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | ||
| Zeile 452: | Zeile 453: | ||
2. Ein Mädchen wird gelost. | 2. Ein Mädchen wird gelost. | ||
Die | Die Wahrscheinlichkeiten ergeben sich aus den absoluten Häufigkeiten, also der tatsächlichen Anzahl an Jungen und Mädchen geteilt durch die Anzahl der Schülerinnen und Schüler in der Klasse. Das Baumdiagramm sieht dann so aus: | ||
[[Datei:Baumdiagramm A1 a.jpg|zentriert]] | [[Datei:Baumdiagramm A1 a.jpg|zentriert]] | ||
| Zeile 471: | Zeile 472: | ||
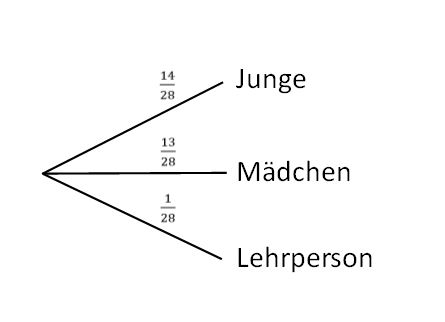
3. Die Lehrperson wird gelost. | 3. Die Lehrperson wird gelost. | ||
Auch hier ergeben sich die Wahrscheinlichen aus den absoluten | Auch hier ergeben sich die Wahrscheinlichen aus den absoluten Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt 28 Personen zur Auswahl. Das Baumdiagramm sieht so aus: | ||
[[Datei:Baumdiagramm A1 b.jpg|zentriert]] | [[Datei:Baumdiagramm A1 b.jpg|zentriert]] | ||
| Zeile 481: | Zeile 482: | ||
{{Box | Komplementärregel| | {{Box | Komplementärregel| | ||
Hat ein Experiment genau zwei | Hat ein Experiment genau zwei Ereignisse, so spricht man von Ereignis und Gegenereignis. Die Wahrscheinlichkeiten der beiden ergeben in der Summe 1: | ||
<math>P(E)+P(\bar E)=1</math> | <math>P(E)+P(\bar E)=1</math> | ||
| Zeile 487: | Zeile 488: | ||
| Merksatz}} | | Merksatz}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 7: Schulfest | Bei eurem Schulfest gibt es eine Tombola. Es geht darum, aus einem Glas eine Kugel zuziehen. Bevor du ohne hinzuschauen ziehen darfst, wird dir einmal der Inhalt des Glases gezeigt, du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf die Bilder klicken, um sie in vergrößerter Form zu sehen. | ||
[[Datei:Urne A2 1.jpg|mini|Abbildung 1]][[Datei:Plakat.jpg|mini|Abbildung 2]] | [[Datei:Urne A2 1.jpg|mini|Abbildung 1]][[Datei:Plakat.jpg|mini|Abbildung 2]] | ||
| Zeile 521: | Zeile 522: | ||
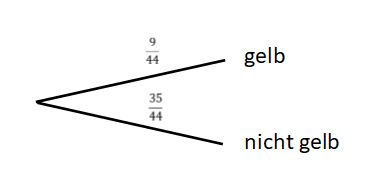
2. Die Kugel ist nicht gelb. | 2. Die Kugel ist nicht gelb. | ||
Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der absoluten Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist | Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der absoluten Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist erfolgt aus der Komplementärregel. | ||
Das Baumdiagramm sieht dann so aus: | Das Baumdiagramm sieht dann so aus: | ||
| Zeile 580: | Zeile 581: | ||
{{Box |Pfadmultiplikationsregel| | {{Box |Pfadmultiplikationsregel| | ||
Bei der Pfadmultiplikationsregel werden die Wahrscheinlichkeiten der aufeinanderfolgenden Ereignisse miteinander | Bei der Pfadmultiplikationsregel werden die Wahrscheinlichkeiten der aufeinanderfolgenden Ereignisse miteinander multipliziert. | ||
[[Datei:Pfadregel Multiplikation.jpg|zentriert]] | [[Datei:Pfadregel Multiplikation.jpg|zentriert]] | ||
| Zeile 589: | Zeile 590: | ||
| Merksatz}} | | Merksatz}} | ||
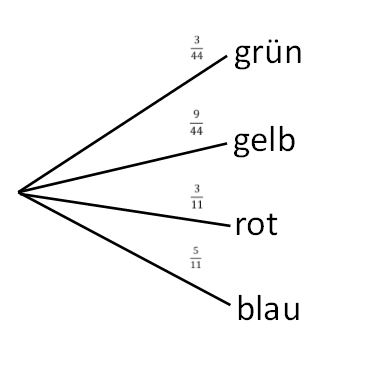
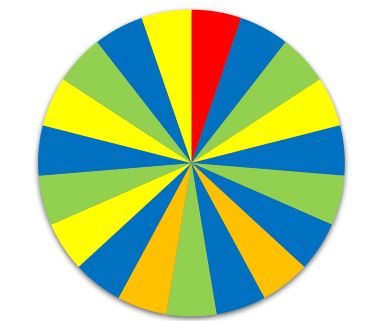
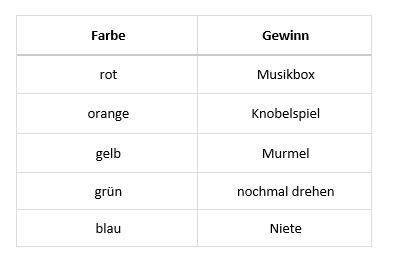
{{Box | Aufgabe | {{Box | Aufgabe 8: Münsteraner Send |Auf dem Münsteraner Send gibt es ein Glücksrad. Es sieht wie folgt aus: | ||
[[Datei:Glücksrad A3.jpg|zentriert]] | [[Datei:Glücksrad A3.jpg|zentriert]] | ||
| Zeile 610: | Zeile 611: | ||
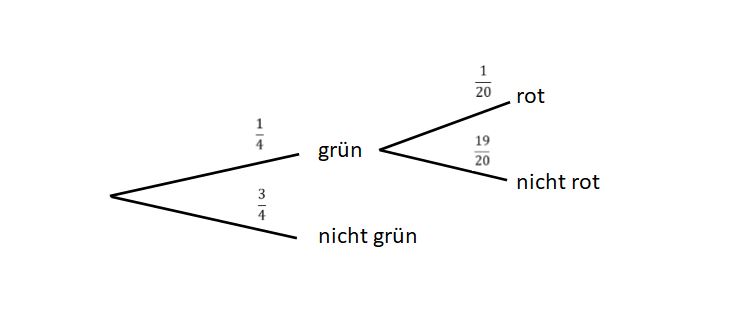
Hier wurden die Brüche bereits gekürzt. | Hier wurden die Brüche bereits gekürzt. | ||
Mit der | Mit der Pfadmultiplikationsregel gilt nun: | ||
<math> P(\text{grün}|\text{rot})=\tfrac{1}{4}\cdot\tfrac{1}{20}=\tfrac{1}{80} </math> | <math> P(\text{grün}|\text{rot})=\tfrac{1}{4}\cdot\tfrac{1}{20}=\tfrac{1}{80} </math> | ||
| Zeile 618: | Zeile 619: | ||
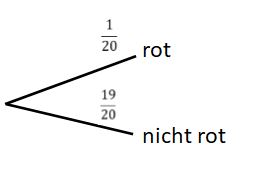
'''b)''' Ist der Fall aus a wahrscheinlicher als der, beim ersten Mal Drehen auf einem roten Feld zu landen? | '''b)''' Ist der Fall aus a wahrscheinlicher als der, beim ersten Mal Drehen auf einem roten Feld zu landen? | ||
{{Lösung versteckt|1= Du brauchst hier nur noch berechnen, wie groß die | {{Lösung versteckt|1= Du brauchst hier nur noch berechnen, wie groß die Wahrscheinlichkeit ist, direkt beim ersten Mal auf dem roten Feld zu landen. |2= Tipp |3= Tipp}} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 656: | Zeile 657: | ||
| Merksatz}} | | Merksatz}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 9: Kartenspiel | | ||
Bei einem Skatkartenspiel gibt es 12 Bildkarten. Es gibt 4 Buben, 4 Damen und 4 Könige. Karo und Herz werden auch „rote Karten“ genannt und Pik und Kreuz auch „schwarze Karten“. Berechne nun die Wahrscheinlichkeit, mit der du die angegebene Karte aus den 32 Spielkarten ziehst. | Bei einem Skatkartenspiel gibt es 12 Bildkarten. Es gibt 4 Buben, 4 Damen und 4 Könige. Karo und Herz werden auch „rote Karten“ genannt und Pik und Kreuz auch „schwarze Karten“. Berechne nun die Wahrscheinlichkeit, mit der du die angegebene Karte aus den 32 Spielkarten ziehst. | ||
| Zeile 697: | Zeile 698: | ||
{{Box | Aufgabe | {{Box | Aufgabe 10: Scrabble| | ||
Bei einem Spieleabend wird Scrabble gespielt. Sieh dir die beiden bereits gelegten Wörter an. Die dafür verwendeten Steine werden in einen leeren Sack gelegt. Gehe davon aus, dass die Spielsteine alle dieselbe Größe und Beschaffenheit haben. | Bei einem Spieleabend wird Scrabble gespielt. Sieh dir die beiden bereits gelegten Wörter an. Die dafür verwendeten Steine werden in einen leeren Sack gelegt. Gehe davon aus, dass die Spielsteine alle dieselbe Größe und Beschaffenheit haben. | ||
| Zeile 748: | Zeile 749: | ||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
{{Box | Aufgabe | {{Box | Aufgabe 11: Würfeln | | ||
Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | ||
| Zeile 790: | Zeile 791: | ||
| Arbeitsmethode }} | | Arbeitsmethode }} | ||
{{Box | Aufgabe | {{Box | Aufgabe 12: Mensch ärgere dich nicht | | ||
Markus und Julia spielen „Mensch ärgere dich nicht“. Sieh dir die aktuelle Spielsituation an. | Markus und Julia spielen „Mensch ärgere dich nicht“. Sieh dir die aktuelle Spielsituation an. | ||
| Zeile 843: | Zeile 844: | ||
P(E) = <math>\tfrac{1}{6}</math> + <math>\tfrac{1}{6}</math> + <math>\tfrac{1}{6}</math> = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{3}{6}</math> = <math>\tfrac{1}{2}</math> | P(E) = <math>\tfrac{1}{6}</math> + <math>\tfrac{1}{6}</math> + <math>\tfrac{1}{6}</math> = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{3}{6}</math> = <math>\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
2. Fall: Julia würfelt eine 2 | 2. Fall: Julia würfelt eine 2 | ||
| Zeile 853: | Zeile 854: | ||
P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
3. Fall: Julia würfelt eine 3 | 3. Fall: Julia würfelt eine 3 | ||
| Zeile 863: | Zeile 864: | ||
P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
4. Fall: Julia würfelt eine 4 | 4. Fall: Julia würfelt eine 4 | ||
| Zeile 873: | Zeile 874: | ||
P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | P(E) = 3 * <math>\tfrac{1}{6}</math> = <math>\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
Wenn also beide einmal an der Reihe waren ohne ins Haus zu setzen, ist die Wahrscheinlichkeit dann für beide gleich beim nächsten Zug ins Haus zu kommen. Sie beträgt | Wenn also beide einmal an der Reihe waren ohne ins Haus zu setzen, ist die Wahrscheinlichkeit dann für beide gleich beim nächsten Zug ins Haus zu kommen. Sie beträgt <math>\tfrac{1}{2}</math>. | ||
|2=Lösung b)|3=Lösung}} | |2=Lösung b)|3=Lösung}} | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
Version vom 21. November 2020, 10:02 Uhr
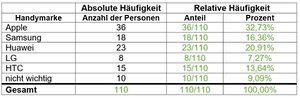
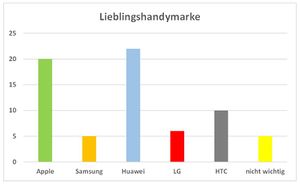
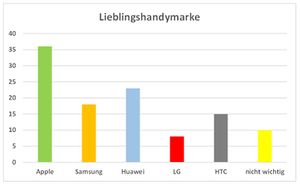
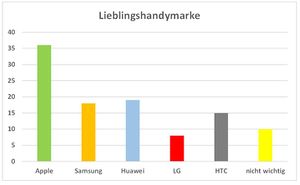
Absolute und relative Häufigkeit
Zufallsexperimente
Laplace-Experimente