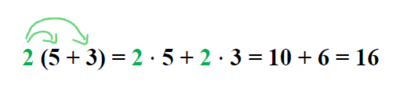Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 331: | Zeile 331: | ||
</div> | </div> | ||
{{Box | 1=Aufgabe 3: Natüüürlich | 2=Gegeben sind nun allgemein zwei aufeinander folgende Zahlen a und b mit | {{Box | 1=Aufgabe 3: Natüüürlich | 2=Gegeben sind nun allgemein zwei aufeinander folgende Zahlen a und b mit | ||
<math> b = a-1 </math>. Begründe, dass die folgende Rechenregel immer stimmt: | <math> b = a-1 </math>. <br /> | ||
Die Differenz <math> a^2-b^2 </math> ist gleich der Summe <math> a+b </math>. | 3=Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | Begründe unter Verwendung einer binomischen Formel, dass die folgende Rechenregel immer stimmt: | ||
Die Differenz <math> a^2-b^2 </math> ist gleich der Summe <math> a+b </math>. Notiere deinen Lösungsweg in dein Heft. | |||
{{Lösung versteckt|1=Bilde eine Gleichungskette <math> a^2-b^2 = ... = a+b </math> 2=Tipp 1|3=Tipp verbergen}} | |||
{{Lösung versteckt|1=Verwende bei der Umformung die dritte binomische Formel. 2=Tipp 2|3=Tipp verbergen}} | |||
{{Lösung versteckt|1= | |||
Zunächst wird die 3. binomische Formel ausgenutzt: <br /> | |||
<div align="center"> <math> a^2-b^2 = (a-b)(a+b) </math> <div> <br /> | |||
Dann wird für <math> b = a-1 </math> eingesetzt: <br /> | |||
<div align="center"> <math> = (a-(a-1))(a+(a-1)) </math> <div> <br /> | |||
Nun die erste Klammer auflösen: <br /> | |||
<div align="center"> <math> = 1 \cdot (a+(a-1)) </math> <div> <br /> | |||
Schließlich für <math> a-1 = b </math> einsetzen: <br /> | |||
<div align="center"> <math> = 1 \cdot (a+(b)) = a+b </math> <div> <br /> <br /> | |||
Alternativ: | |||
<math> a^2-b^2 = (a+b)(a-b) = (a+b) \cdot 1 = a+b </math>. | |||
2=Lösung|3=Lösung verbergen}} | |||
| 3=Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | |||
Version vom 20. November 2020, 18:31 Uhr
1) Terme zusammenfassen
Einführung
Wie kann ich Terme zusammenfassen?
Aufgabenteil
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Einführung
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgabenteil
| 1. binomische Formel | |||
| 2. binomische Formel | |||
| 3. binomische Formel | |||
| Das ist keine binomische Formel |
a)15()a()
b)3a()4b()3a()4b())
c)9u()2()
d)2m()7()
e)8y()10z()
f)6u()17w()6u()17w())