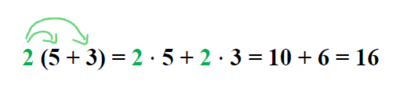Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 219: | Zeile 219: | ||
{{Box | 1=Übung: Binomische Formeln herleiten | 2=Versuche, die erste binomische Formel in deinem Heft rechnerisch herzuleiten. Stelle dazu eine Gleichungskette der Form <math> (a+b)^2 = ... = a^2+2ab+b^2 </math> auf. | {{Box | 1=Übung: Binomische Formeln herleiten | 2=Versuche, die erste binomische Formel in deinem Heft rechnerisch herzuleiten. Stelle dazu eine Gleichungskette der Form <math> (a+b)^2 = ... = a^2+2ab+b^2 </math> auf. | ||
{{Lösung versteckt|1=Beginne mit dem Ausgangsterm <math>(a+b)^2</math> und schreibe die Potenz wiefolgt aus: <math>(a+b)\cdot(a+b)</math>. Dies kannst du nun nach den bekannten Regeln ausmultiplizieren.|2=Tipp|3=Tipp ausblenden}} | {{Lösung versteckt|1=Beginne mit dem Ausgangsterm <math>(a+b)^2</math> und schreibe die Potenz wiefolgt aus: <math>(a+b)\cdot(a+b)</math>. Dies kannst du nun nach den bekannten Regeln ausmultiplizieren.|2=Tipp|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=(<math>{\color{green}a}+{\color{blue}b})^2 = ({\color{green}a}+{\color{blue}b})\cdot({\color{green}a}+{\color{blue}b}) = {\color{green}a}{\color{green}a}+{\color{green}a}{\color{blue}b}+{\color{blue}b}{\color{green}a}+{\color{blue}b}{\color{blue}b} = {\color{green}a}^2+2{\color{green}a}{\color{blue}b}+{\color{blue}b}^2</math>|2=Lösung|3=Lösung ausblenden}}| 3=Übung}} | {{Lösung versteckt|1=(<math>{\color{green}a}+{\color{blue}b})^2</math> Zunächst beginnt man mit dem Augangsterm <br /> = <math>({\color{green}a}+{\color{blue}b})\cdot({\color{green}a}+{\color{blue}b})</math> Nun wird die Potenz ausgeschrieben <br /> = <math>{\color{green}a}{\color{green}a}+{\color{green}a}{\color{blue}b}+{\color{blue}b}{\color{green}a}+{\color{blue}b}{\color{blue}b}</math> Als nächstes werden die Klammern ausmultipliziert <br /> = <math>{\color{green}a}^2+2{\color{green}a}{\color{blue}b}+{\color{blue}b}^2</math> Das Kommutativgesetz (Vertauschungsgesetz) liefert das Ergebnis.|2=Lösung|3=Lösung ausblenden}}| 3=Übung}} | ||
=====Herleitung über Flächen von Quadraten===== | =====Herleitung über Flächen von Quadraten===== | ||
Version vom 19. November 2020, 08:41 Uhr
1) Terme zusammenfassen
Einführung
Wie kann ich Terme zusammenfassen?
Aufgabenteil
Zuerst musst du die Klammern auflösen, dann die Summanden nach ihren Variablen ordnen. Danach musst du noch die Brüche gleichnamig machen um danach alles zusammenfassen zu können.
| 5a+5 | ||
| a+2 | 3a+1 | |
| 3a-4 |
Berechne zuerst die Summe der ersten Spalte. Diese Summe muss auch die Summe aller weiteren Zeilen, Spalten und Diagonalen sein
Wenn du die Summe der ersten Spalte berechnet hast, kannst du als nächstes die Summe der zweiten Zeile berechnen und in das noch auszufüllende Kästchen der zweiten Zeile den Term eintragen, der in der Summe noch fehlt, damit die Summe der ersten Spalt gleich der Summe der zweiten Zeile ist.
{
}
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Einführung
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Herleitung über Flächen von Quadraten