Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung

Inhaltsübersicht

a) Unterscheidung Tangente, Sekante und Normale - Aufgabe 1
b) Zuordnungsaufgaben bezüglich der Tangentensteigung - Aufgabe 2, 3, 4 und 5
c) Untersuchung einer Funktion - Aufgabe 6, 7, 8 und 9

Aufgabe 1: Kannst du die Begriffe unterscheiden?

a) Unterscheidung Tangente, Sekante und Normale

---

b) Zuordnungsaufgaben bezüglich der Tangentensteigung

Aufgabe 5: Memory. Wie fit bist du beim Behalten von Graphen und einer Steigung in einem Punkt?

---

c) Untersuchung einer Funktion

Aufgabe 7: Raupenfahrt

<popup name="Lösung"> Die Steigfähigkeit der Raupe liegt mit 76% über der Steigung von 75%. </popup>

---

Aufgabe 8: Muss es in jedem Punkt einer Funktion eine Tangente geben?!

Klicke gleich auf den nebenstehenden Link, um Geogebra zu öffnen. [Geogebra]

Gebe folgende Funktion ein: f(x) = $\sqrt{1-x^2}$

Du siehst dann einen Halbkreis. Überlege kurz, warum die Funktion nur im Intervall von [-1,1] definiert ist.

a) An welchen Punkten kannst du eine Tangente anlegen? An welchen Punkten ergibt es keinen Sinn eine Tangente anzulegen und warum? <popup name="Tipp zu a)">Benutze die h-Methode für einen Punkt, an dem eine Tangente nicht möglich ist. Benutze den Differentialquotienten. </popup>

b) Welche Schlussfolgerung kannst du ziehen, wenn an einer Funktion bereits an einer Stelle keine Tangente angelegt werden kann?

<popup name="Lösung a)"> An fast allen Punkten im Intevall [-1,1] können Tangenten angelegt werden. Die Ausnahmen bilden die Punkte P(-1|0) und Q(1|0). Wir wollen euch dies im Punkt Q einmal exemplarisch zeigen.

Fläche 1

Ihr seht, dass der für h gegen 0 der Zähler gegen 2 und der Nenner gegen 0 geht. Es existiert kein fester Grenzwert, da es gegen unendlich läuft.

</popup>

<popup name="Lösung b)"> Wenn eine Funktion, wie hier in diesem Beispiel, bereits in einem Punkt keine Tangente ausweisen kann, ist sie nicht differenzierbar.
Eine Tangente repräsentiert eine lineare Funktion. Die Steigung einer linearen Funktion muss eine reelle Zahl sein, ansonsten ist die lineare Funkion nicht definiert.

</popup>

---

Aufgabe 9: Kann es in einem Punkt einer Funktion zwei oder mehr Tangenten geben?!

Klicke gleich auf den nebenstehenden Link. [Geogebra]

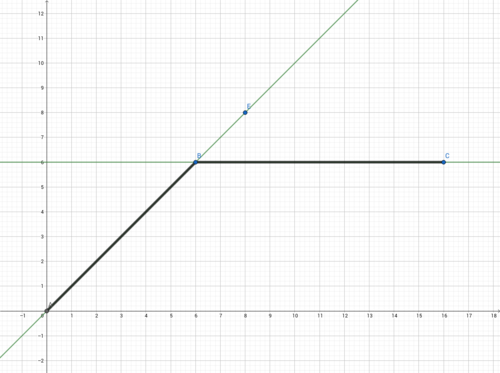
Verbinde mit Hilfe einer Strecke die Punkte (0|0), (6|6); (6|6), (16|6).

a) Welche Tangente(n) würdest du im Punkt P(6|6) einzeichnen?

b) Zeichne zu den jeweiligen Intervallen ([0;6] und [6;16]) die Steigung ein. Wie verläuft die Steigung und was passiert im Punkt P(6|6)?

<popup name="Lösung a)">

Im Punkt P(6|6) gibt es keine eindeutige Tangente. Je nachdem ob man die Steigung von links oder von rechts betrachte, erhält man eine andere, wie im Graph zu sehen ist.

</popup>

<popup name="Lösung b)"> Die Steigung verläuft im Intervall [0;6] und [6;16] linear. Jedoch gibt es im Punkt P(6|6) einen Sprung. Hier ist die neue Funktion also nicht zusammenhängend (Sprungstelle) und daher auch nicht differenzierbar.

Fläche 1

</popup>