Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Graphisches Ableiten - Die Ableitung als Funktionsdetektor: Unterschied zwischen den Versionen
K (katfix) |
Jan (Diskussion | Beiträge) K (1 Version importiert) |
(kein Unterschied)
| |
Version vom 28. Dezember 2018, 11:12 Uhr
In diesem Lernpfad könnt ihr den Zusammenhang zwischen Funktionsgraph und Ableitungsgraph üben und vertiefen. Es steht das graphische Ableitung im Vordergrund, d.h. der Zusammenhang zwischen besonderen Punkten und Merkmalen der Funktion und der Ableitung. Dabei unterscheiden wir zwischen Förder- und Forderaufgaben.
Fällt dir das Thema leicht, konzentriere dich auf die Forderaufgaben (Aufgabe 4 und Aufgabe 5 ).
Hast du noch Schwierigkeiten, konzentriere dich auf die Förderaufgaben (Aufgabe 1 und Aufgabe 2 und Aufgabe 3).
Wenn du bei den Aufgaben Hilfe benötigst, findest du unter den Aufgaben Hilfestellungen. Diese kannst du anklicken. Bei manchen Aufgaben findest du dort auch die Lösungen.
Aufgabe 1: Lückentext (Förderaufgabe)
Um den Graphen größer zu sehen und somit die Werte besser zu erkennen, klicke den Graphen an. Wenn du die Aufgabe gelöst hast, klicke zur Kontrolle unten rechts auf den Haken.
<popup name="Hilfestellung 1">Die Steigung der Tangente entspricht der Steigung des Funktionsgraphen am Berührungspunkt.
</popup>
<popup name="Hilfestellung 2">Besitzt der Funktionsgraph einen Hoch- oder Tiefpunkt, so hat die Tangente keine Steigung. </popup>
<popup name="Hilfestellung 3">Welchen Grad besitzt die Ableitung der Funktion f(x)=x2?.<popup name="Lösung"> Der Grad dieser Ableitung beträgt 1. Versuche dieses nun auf eine Funktion vom Grad 3 zu übertragen.</popup>
Aufgabe 2: Welche Ableitung gehört zu welchem Funktionsgraphen? (Förderaufgabe)
Um den Graphen größer zu sehen und somit die Werte besser zu erkennen, klicke den Graphen an. Wenn du die Aufgabe gelöst hast, klicke zur Kontrolle unten rechts auf den Haken.
<popup name="Hilfestellung 1">Betrachte zunächst auffällige Punkte des Funktionsgraphen und versuche diese Punkte im Ableitungsgraphen wieder zu erkennen.
</popup>
<popup name="Hilfestellung 2">Was sagt eine Nullstelle im Ableitungsgraphen aus? <popup name="Lösung">Eine Nullstelle im Ableitungsgraphen stellt einen Hoch- oder Tiefpunkt im Funktionsgraphen dar. </popup>
<popup name="Hilfestellung 3">Was sagt ein Hoch- oder Tiefpunkt im Ableitungsgraphen aus? <popup name="Lösung"> Ein Hoch- oder Tiefpunkt im Ableitungsgraphen stellt eine Wendestelle im Funktiongraphen dar. </popup>
<popup name="Hilfestellung 4"> Was weißt du über den Ableitungsgraphen, wenn der Funktionsgraph monoton steigt? <popup name="Lösung"> Der Ableitungsgraph verläuft im positiven Bereich des Koordinatensystems.
</popup>
Aufgabe 3: Die 1.000.000 Euro Frage (Förderaufgabe)
Um die Funktionsgraphen größer zu sehen, kannst du diese anklicken. Wenn du die Aufgabe gelöst hast, klicke zur Kontrolle unten rechts auf den Haken.
<popup name="Hilfestellung 1">Versuche zunächst den Graphen der beschriebenen Funktion auf einem Blatt zu zeichnen. </popup>
<popup name="Hilfestellung 2">Was sagt eine Nullstelle im Ableitungsgraphen aus? <popup name="Lösung">Eine Nullstelle im Ableitungsgraphen stellt einen Hoch- oder Tiefpunkt im Funktionsgraphen dar. </popup>
<popup name="Hilfestellung 3">Was sagt ein Hoch- oder Tiefpunkt im Ableitungsgraphen aus? <popup name="Lösung"> Ein Hoch- oder Tiefpunkt im Ableitungsgraphen stellt eine Wendestelle im Funktiongraphen dar. </popup>
<popup name="Lösungsvorschlag">
Die gesuchte Ableitung ist die linke Abbildung.
Die Funktion hat an der Stelle x=3 eine Wendestelle, da sie dort die stärkste Steigung aufweist. Wenn die Funktion eine Wendestelle besitzt, so hat die Ableitung einen Hoch- oder Tiefpunkt. Die linke und rechte Abbildung erfüllen dieses Kriterium. Die mittlere Abbildung kommt nun nicht mehr in Frage.
Da die Funktion einen Hochpunkt bei (2,1) und einen Tiefpunkt bei (4,-1) besitzt, muss die zugehörige Ableitung an den Stellen x=2 und x=4 Nullstellen besitzen. Auch dies ist bei der linken und rechten Abbildung der Fall.
Im Intervall 2 < x <4 fällt die beschriebene Funktion monoton, da sie in (2,1) einen Hochpunkt und in (4,-1) einen Tiefpunkt besitzt. Wenn die Funktion monoton fällt, so ist die Ableitung negativ.
Nun kommt lediglich die linke Abbildung in Frage, da die rechte Ableitung im obigen Intervall positiv ist.
</popup>
Aufgabe 4: Pärchenbildung (Forderaufgabe)
Wenn du die Aufgabe gelöst hast, klicke zur Kontrolle unten rechts auf den Haken.
<popup name="Hilfestellung 1"> Zeichne eine Funktion dritten Grades. Ebenso zeichne die ersten drei Ableitungen von dieser und überlege, welche Zusammenhänge dir auffallen. Wenn dir dies noch Probleme bereitet, schaue dir die Hilfestellung 2 an.
</popup>
<popup name="Hilfestellung 2"> :::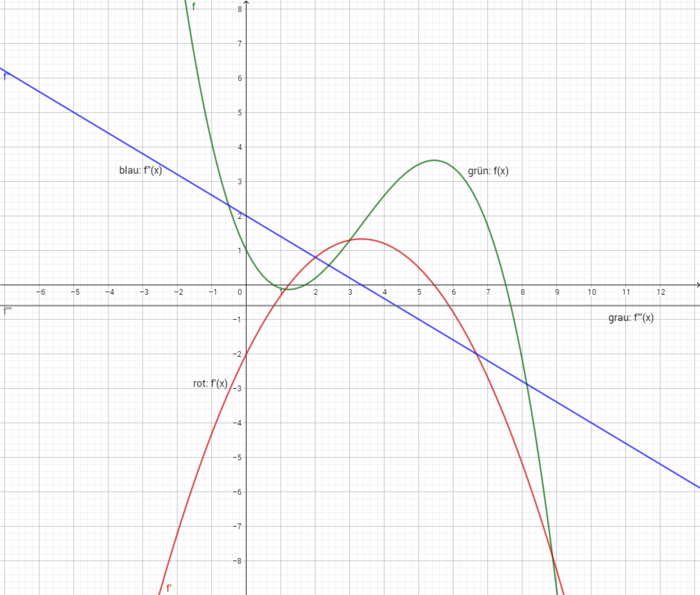 </popup>
<popup name="Hilfestellung 3"> f(x) hat eine Tiefpunkt, wenn die Steigung der Tangente (also die Steigung der Ableitung) in diesem Punkt gleich 0 ist. Versuche dir dieses graphisch vorzustellen. Versuch dann die erste Ableitung ein weiteres mal graphisch abzuleiten. Welche zusätzliche Bedingung für einen Tiefpunkt fällt dir auf?
</popup>
<popup name="Hilfestellung 3"> f(x) hat eine Tiefpunkt, wenn die Steigung der Tangente (also die Steigung der Ableitung) in diesem Punkt gleich 0 ist. Versuche dir dieses graphisch vorzustellen. Versuch dann die erste Ableitung ein weiteres mal graphisch abzuleiten. Welche zusätzliche Bedingung für einen Tiefpunkt fällt dir auf?
Dieses Verfahren kannst du auch auf einen Hochpunkt anwenden.
</popup>
<popup name="Hilfestellung 4"> Die Wendestelle gibt die stärkste Steigung des Funktionsgraphen an. Dies bedeutet, dass die Ableitung die Steigung des Funktionsgraphen angibt.
Denke daran, dass die zweite Ableitung die Steigung der ersten Ableitung angibt. Demnach bedeutet der Hoch-/Tiefpunkt der ersten Ableitung eine Nullstelle in der zweiten Ableitung. Versuche nun durch zeichnen der dritten Ableitung die weitere Bedingung für die dritte Ableitung herauszubekommen.
</popup>
Aufgabe 5: Temperatur im Jahresverlauf (Forderaufgabe)
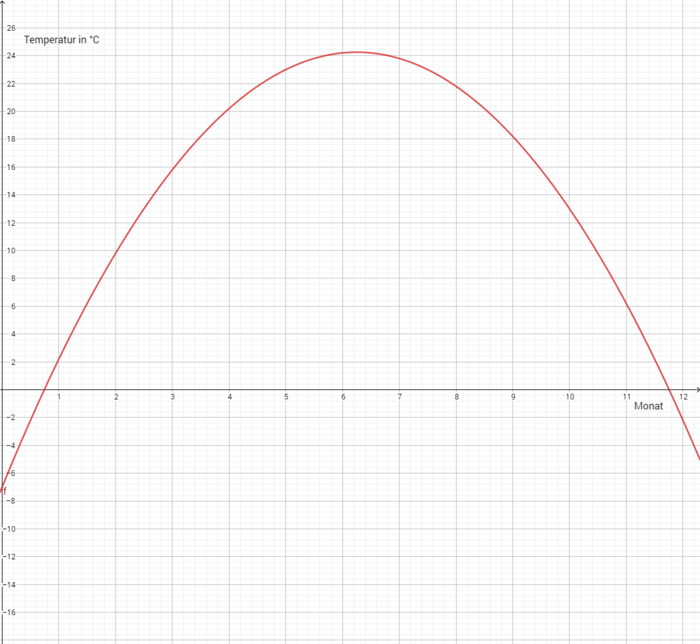
Der unten dargestellte Graph f stellt die durchschnittliche Tagestemperatur im Jahr 2016 in Deutschland dar. Auf der x-Achse sind die Monate von 0 bis 12 darstellt, wobei 0 den 1.Januar, 1 den 1.Februar, …, 11 den 1.Dezember darstellt. Auf der y-Achse ist die Temperatur in °C angegeben.
a.) Zeichne den zugehörigen Ableitungsgraphen in dein Heft und beschreibe schrittweise, wie du ihn konstruiert hast. Was stellt der Ableitungsgraph im Sachkontext dar?
<popup name="Hilfestellung 1"> Suche zunächst wichtige Punkte heraus (wie z.B. Hochpunkt, Wendestellen, Nullstellen) und überlege, welche Bedeutung diese für den Ableitungsgraphen haben? Wenn dir diese Hilfestellung noch Probleme bereitet, schaue dir Aufgabe 2 an. </popup>
<popup name="Hilfestellung 2"> Der Funktionsgraph kann durch die Gleichung f(x) = -0,8x2 + 10x - 7 modelliert werden. Welcher Grad liegt dann bei der Ableitung vor? <popup name="Lösung"> Der Ableitungsgraph stellt eine Gerade dar.
</popup>
<popup name="Lösungsvorschlag"> Die dargestellte Gerade ist der Ableitungsgraph f' von f.
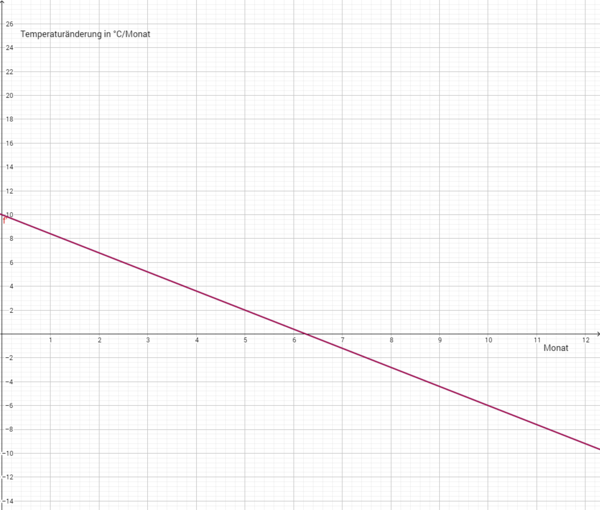
Beispielhafte Konstruktion:
1.) Es liegt eine Funktion zweiten Grades vor. Also hat die Ableitung den Grad 1. Sie ist also eine Gerade.
2.) Der Hochpunkt liegt ungefähr bei (6,2|24,2). Also liegt eine Nullstelle bei x=6,2 vor.
3.) Der Funktionsgraph steigt im Intervall [0;6,2) monoton. Demnach ist die Ableitung in diesem Intervall positiv. Je stärker der Funktionsgraph steigt, desto positiver ist der Ableitungsgraph.
4.) Der Funktionsgraph fällt im Intervall (6,2;12] monoton. Demnach ist die Ableitung in diesem Intervall negativ. Je stärker der Funktionsgraph fällt, desto negativer ist der Ableitungsgraph
Ableitung im Sachkontext:
Die Ableitung gibt die Temperaturänderung in °C/Monat an.
</popup>
b.) In welchem Monat ist die Temperatur am höchsten?
<popup name="Hilfestellung"> Denke daran, dass x=1 für den 1.Februar steht.
</popup>
<popup name="Lösungsvorschlag"> Die Temperatur ist im Juli am höchsten, denn der Hochpunkt liegt an der Stelle x=6,2.
</popup>
c.) In welchen Monaten steigt bzw. fällt die Temperatur und wann steigt sie am schnellsten an? Versuche dieses mit dem Ableitungsgraphen zu begründen.
<popup name="Hilfestellung"> Überlegt, welche Bedeutung es für den Ableitungsgraphen hat, wenn der Funktionsgraph monoton steigt/fällt. <popup name="Lösung"> Wenn der Funktionsgraph monoton steigt/fällt, verläuft der Ableitungsgraph im positiven/negativen Bereich.
</popup>
<popup name="Lösungsvorschlag"> Die Temperatur steigt in den Monaten Januar bis Juli. Da dort der Ableitungsgraph im positiven Bereich verläuft. Allerdings nimmt die Temperaturzunahme ab, da die angegebenen Werte in °C/Monat weniger positiv werden.
Die Temperatur fällt in den Monaten Juli bis Dezember. Da dort der Ableitungsgraph im nrgativen Bereich verläuft. zusätzlich nimmt die Temperaturabnahme zu, da die angegebenen Werte in °C/Monat negativer werden werden.
Die Temperatur steigt im Monat Januar am stärksten an. Dieses ist daran zu erkenne, dass die Ableitung dort den größten Wert annimmt.
Die Temperatur fällt im Monat Dezember am stärksten an. Dieses ist daran zu erkenne, dass die Ableitung dort den kleinsten Wert annimmt.
</popup>