Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 207: | Zeile 207: | ||
===Knobelaufgaben=== | ===Knobelaufgaben=== | ||
{{Box|1= <span style="color: green">Aufgabe 8: Achterbahn | {{Box|1= <span style="color: green"></span>Aufgabe 8: Achterbahn |2= Du benötigst für die Aufgabe kariertes Papier, Stifte, Lineal und evtl. einen Taschenrechner. | ||
[[Datei:Efteling rollercoaster.jpg|links|thumb|Efteling]] | [[Datei:Efteling rollercoaster.jpg|links|thumb|Efteling]] | ||
| Zeile 232: | Zeile 232: | ||
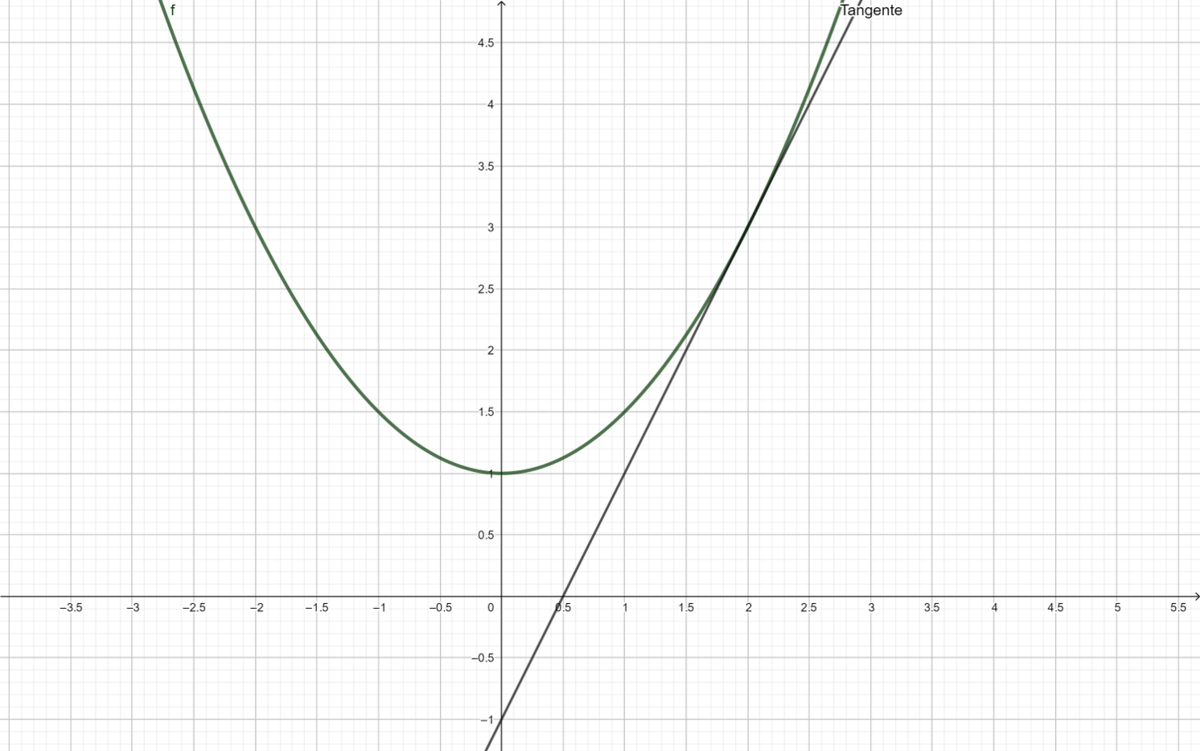
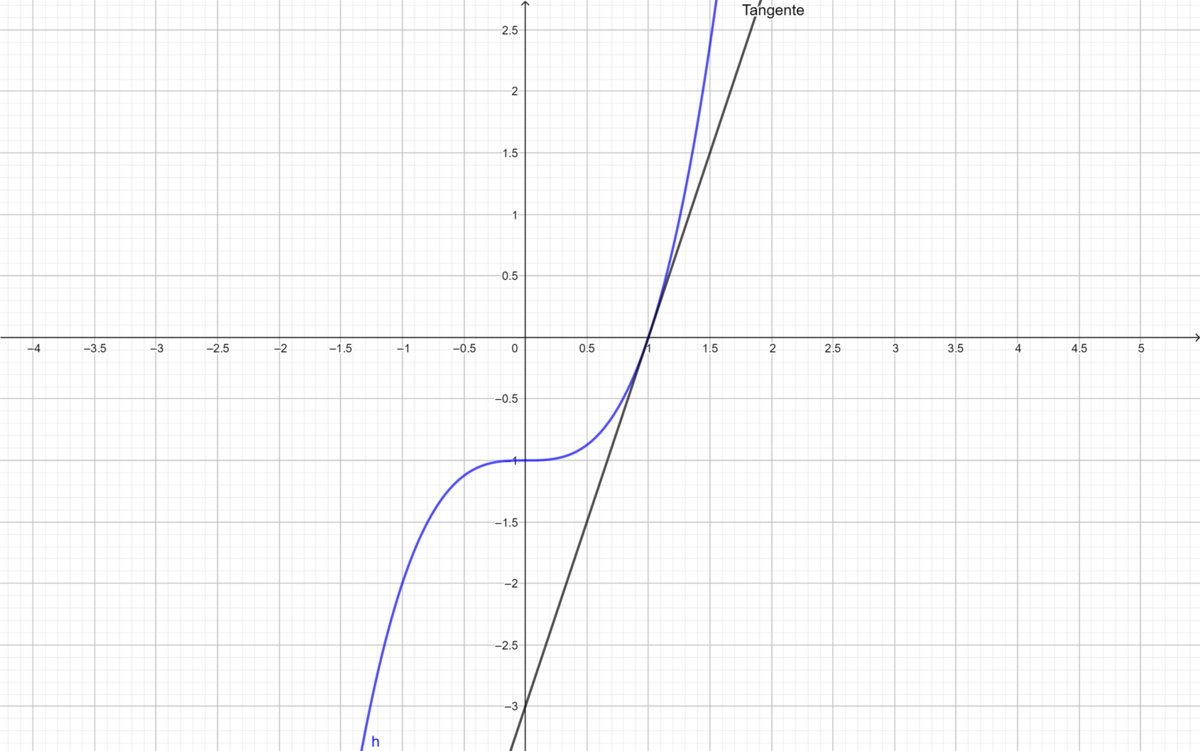
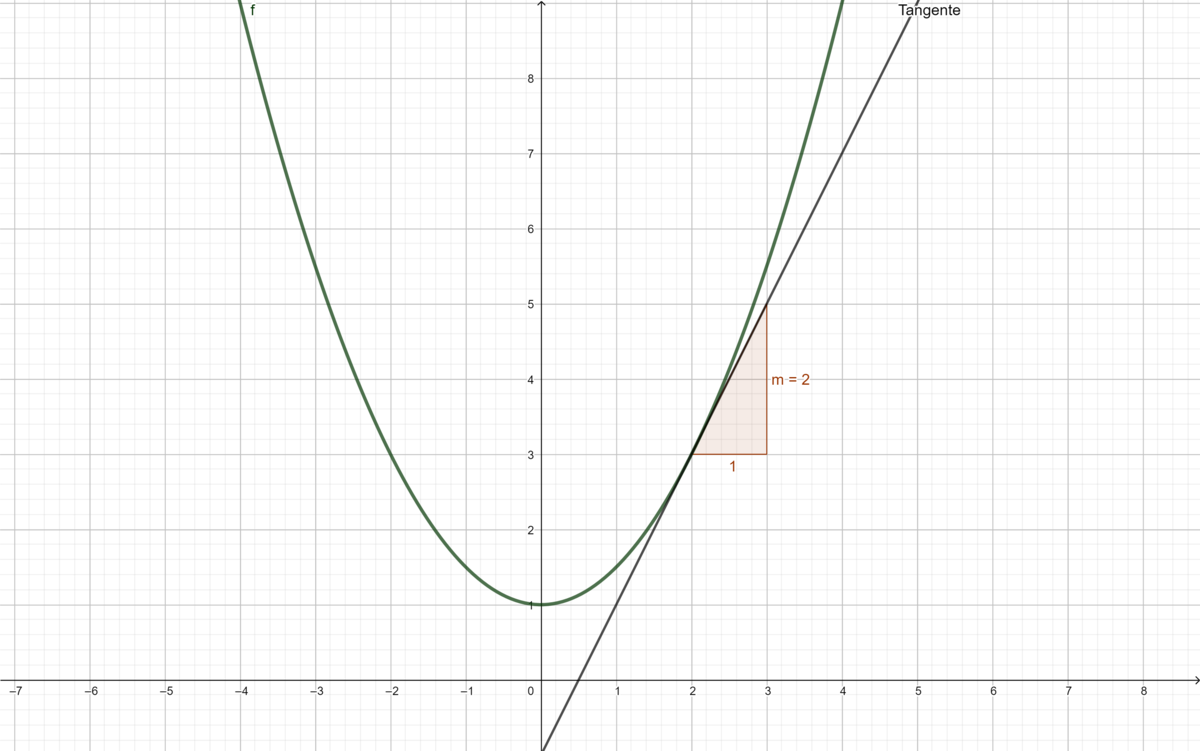
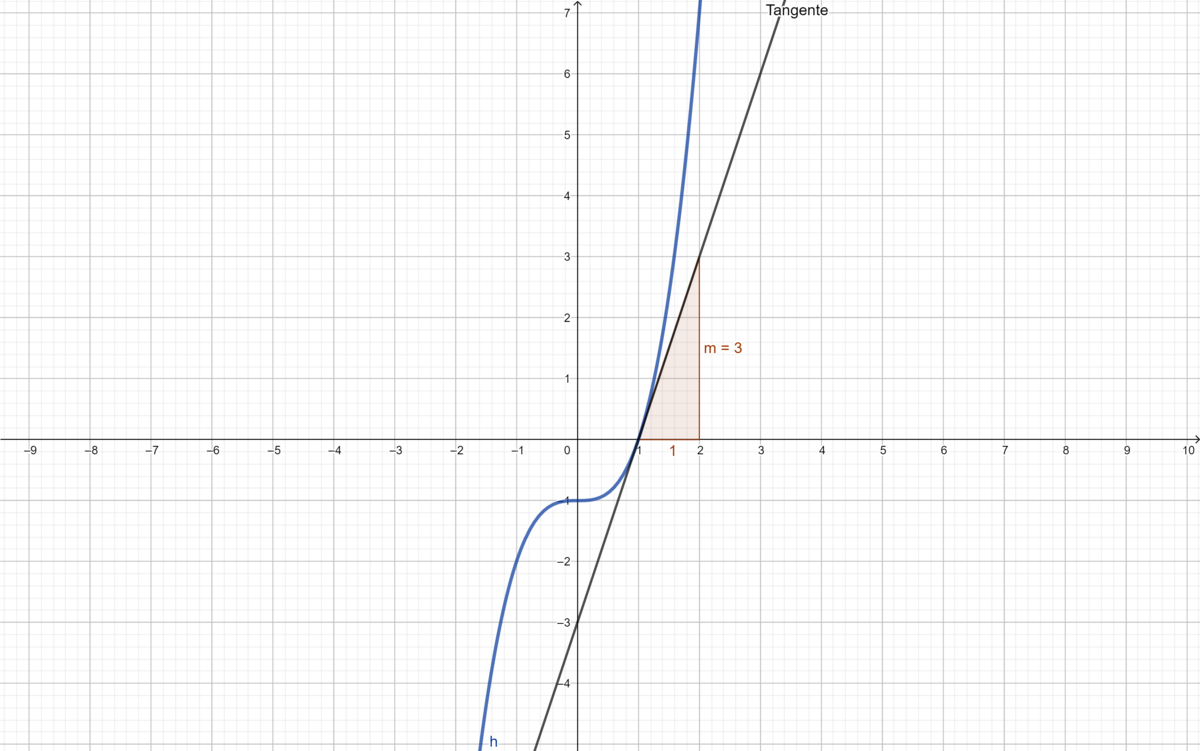
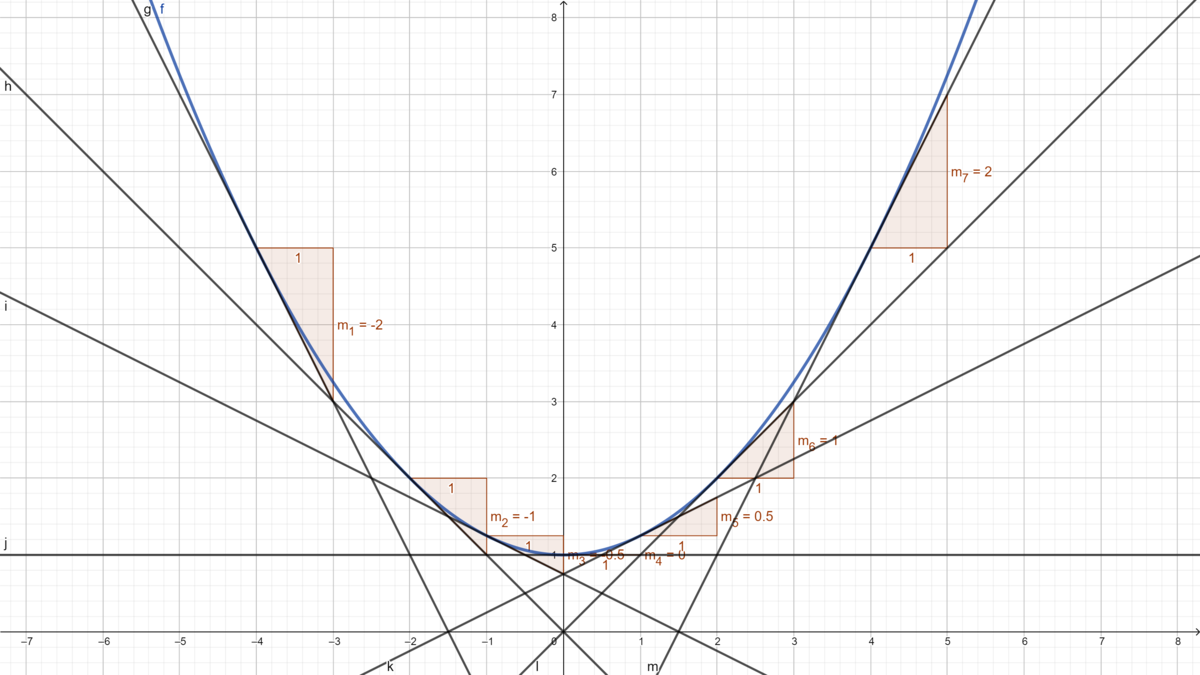
{{Lösung versteckt|1 = Wir benutzen wie bereits in den Aufgaben davor die h-Formeln für den Differentialquotient. <math>f'(x) = \lim_{h \to \ 0} \frac{f(x +h) - f(x)}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}(x +h)^2 + 1 - \tfrac{1}{4}x^2-1}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}x^2 +\tfrac{1}{2} xh+\tfrac{1}{4} h^2- \tfrac{1}{4}x^2}{h} = \lim_{h \to \ 0} ( \tfrac{1}{2}x + \tfrac{1}{4}h) = \tfrac{1}{2}x </math> Das ist die gleiche Funktion wie beim graphischen Differenzieren im Teil b. Die Ableitung ist also die Steigung der Tangente der Funktion in einem bestimmtem Punkt.|2=Lösung|3=Lösung}}|Farbe = {{Farbe|grün|dunkel}} |3= Arbeitsmethode}} | {{Lösung versteckt|1 = Wir benutzen wie bereits in den Aufgaben davor die h-Formeln für den Differentialquotient. <math>f'(x) = \lim_{h \to \ 0} \frac{f(x +h) - f(x)}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}(x +h)^2 + 1 - \tfrac{1}{4}x^2-1}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}x^2 +\tfrac{1}{2} xh+\tfrac{1}{4} h^2- \tfrac{1}{4}x^2}{h} = \lim_{h \to \ 0} ( \tfrac{1}{2}x + \tfrac{1}{4}h) = \tfrac{1}{2}x </math> Das ist die gleiche Funktion wie beim graphischen Differenzieren im Teil b. Die Ableitung ist also die Steigung der Tangente der Funktion in einem bestimmtem Punkt.|2=Lösung|3=Lösung}}|Farbe = {{Farbe|grün|dunkel}} |3= Arbeitsmethode}} | ||
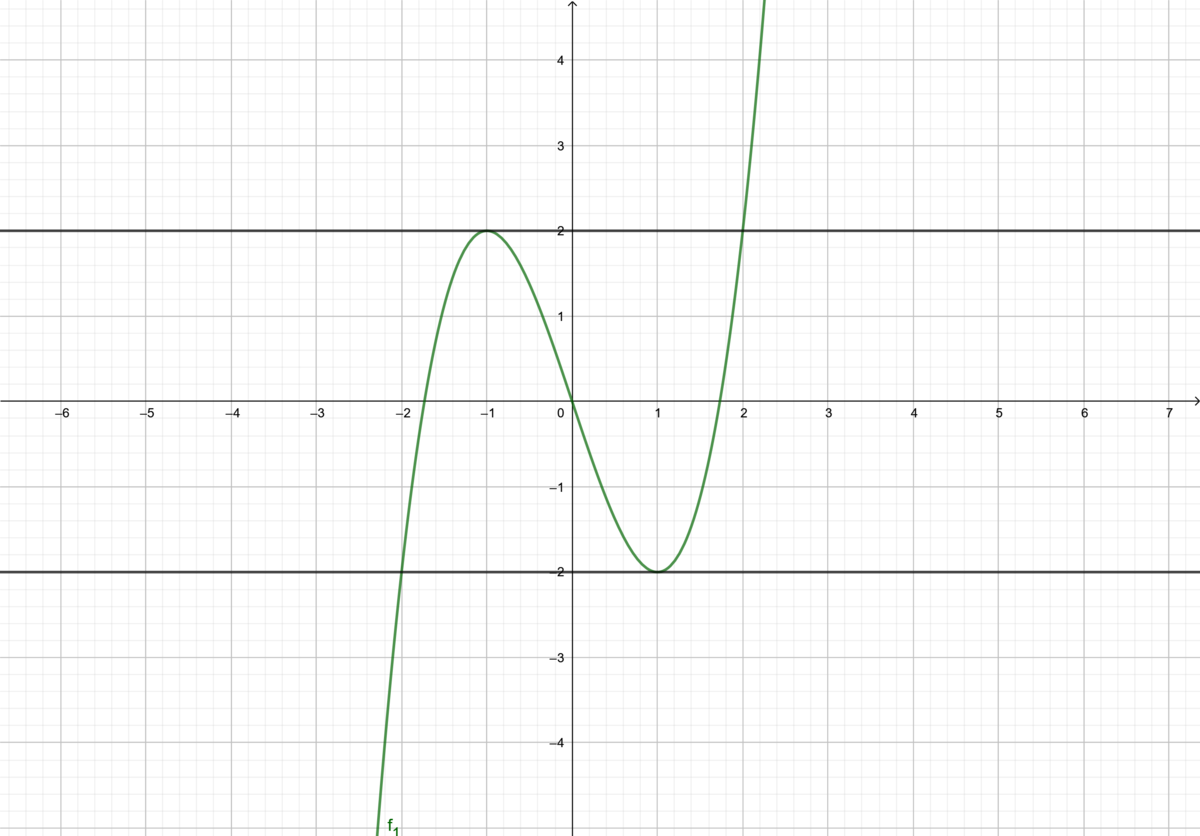
{{Box|1= <span style="color: green"> ⭐Aufgabe 9 | {{Box|1= <span style="color: green"></span> ⭐Aufgabe 9: Tangenten für Funktionenschar |2= Du benötigst für die Aufgabe Papier, Stifte, Lineal und evtl. einen Taschenrechner. | ||
Gegeben ist eine Funktionenschar durch die Gleichung <math>f_t(x) = x^3 - 3t^2x </math> und <math>t>0</math> | Gegeben ist eine Funktionenschar durch die Gleichung <math>f_t(x) = x^3 - 3t^2x </math> und <math>t>0</math> | ||
Version vom 19. Mai 2020, 08:10 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben