Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 132: | Zeile 132: | ||
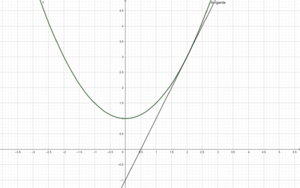
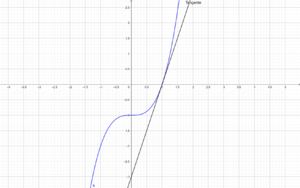
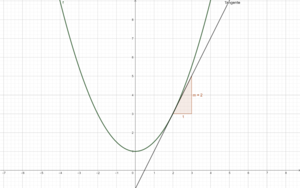
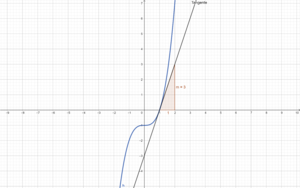
'''''a) Zeichne die Graphen der Funktionen f(x) und h(x) und skizziere die Tangenten in den angegebenen Punkten. ''''' | '''''a) Zeichne die Graphen der Funktionen f(x) und h(x) und skizziere die Tangenten in den angegebenen Punkten. ''''' | ||
{{Lösung versteckt|1=[[Datei:Loesung 5a Funktion f.png|zentriert|width= | {{Lösung versteckt|1=[[Datei:Loesung 5a Funktion f.png|zentriert|width=3000px|height=2600px|rahmenlos]]|2=Skizze f(x)|3=Skizze f(x)}} | ||
{{Lösung versteckt|1=[[Datei:Loesung 5a Funktion h.png|zentriert|width= | {{Lösung versteckt|1=[[Datei:Loesung 5a Funktion h.png|zentriert|width=3000px|height=2600px|rahmenlos]]|2=Skizze h(x)|3=Skizze h(x)}} | ||
'''''b)Bestimme die Steigung der Funktion im gegebenen Punkt durch Ablesen der Tangentensteigung.''''' | '''''b)Bestimme die Steigung der Funktion im gegebenen Punkt durch Ablesen der Tangentensteigung.''''' | ||
| Zeile 140: | Zeile 140: | ||
{{Lösung versteckt|1 = Die Tangente der Funktion <math>f(x)</math> hat an der vorgegebenen Stelle Steigung <math>m=2</math>. Die Tangente der Funktion <math>h(x)</math> hat an der Stelle 1 die Steigung <math>m=3</math> Wie komme ich zu meiner Lösung? Beide Steigungen sind am einfachsten im Intervall [1; 2] abzulesen | {{Lösung versteckt|1 = Die Tangente der Funktion <math>f(x)</math> hat an der vorgegebenen Stelle Steigung <math>m=2</math>. Die Tangente der Funktion <math>h(x)</math> hat an der Stelle 1 die Steigung <math>m=3</math> Wie komme ich zu meiner Lösung? Beide Steigungen sind am einfachsten im Intervall [1; 2] abzulesen | ||
{{Lösung versteckt|1=[[Datei:Steigungf.png|zentriert|width= | {{Lösung versteckt|1=[[Datei:Steigungf.png|zentriert|width=3000px|height=2600px|rahmenlos]]|2=Steigungsdreieck für f(x)|3=Steigungsdreieck für f(x)}} | ||
{{Lösung versteckt|1=[[Datei:Steigungsdreieckf.png|zentriert|width= | {{Lösung versteckt|1=[[Datei:Steigungsdreieckf.png|zentriert|width=3000px|height=2600px|rahmenlos]]|2=Steigungsdreieck für h(x)|3=Steigungsdreieck für h(x)}} | ||
| Zeile 202: | Zeile 202: | ||
{{LearningApp|app=10938377|width=100%|height=600px}} | {{LearningApp|app=10938377|width=100%|height=600px}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= Überlege zuerst welche Begriffe sind dem x-Wert und dem y-Wert zuzuordnen, was also hängt wie von einander ab. Zum Beispiel hängt die zurückgelegte Strecke von der Fahrzeit ab, damit ist schon mal die Funktion beschrieben. Die Formeln für durchschnittliche und momentane (lokale) Änderungsraten findest du in den Merkkästen. |2=Tipp|3=Tipp}} | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
Version vom 17. Mai 2020, 20:52 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben