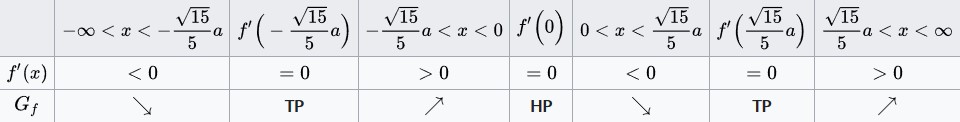Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 43: | Zeile 43: | ||
'''Beispiel: Monotonieverhalten für <math>g(x)=x^2</math> bestimmen ''' | '''Beispiel: Monotonieverhalten für <math>g(x)=x^2</math> bestimmen ''' | ||
Zuerst berechnen wir die Ableitung <math>g'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>g'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>. | Zuerst berechnen wir die Ableitung <math>g'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>g'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>. | ||
Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>(-\infty,0)</math> und <math>(0,+\infty)</math>. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle: | Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>(-\infty,0)</math> und <math>(0,+\infty)</math>. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle: | ||
[[Datei:Monotonietabelle x^2.jpg|zentriert|rahmenlos|1000x1000px]] | [[Datei:Monotonietabelle x^2.jpg|zentriert|rahmenlos|1000x1000px]] | ||
Aus dem Ergebnis können wir schließen, dass die Funktion für <math>(-\infty,0)</math> streng monoton fallend und für <math>(0,+\infty)</math> streng monoton steigend ist. | Aus dem Ergebnis können wir schließen, dass die Funktion für <math>(-\infty,0)</math> streng monoton fallend und für <math>(0,+\infty)</math> streng monoton steigend ist. | ||