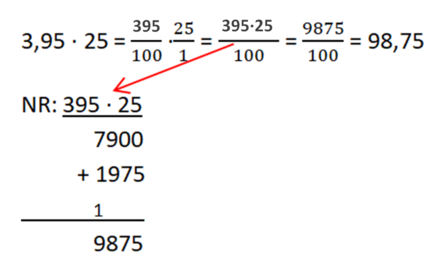Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/2) Dezimalbrüche multiplizieren: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(Lösungen ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 78: | Zeile 78: | ||
Lösung zum Vergleichen (Du musst ausführliche Rechnungen im Heft notiert haben!) a) 5,4 m² b) 15,5 m² |2=Tipp und Lösungen zu Nr. 16|3=Verbergen}} | Lösung zum Vergleichen (Du musst ausführliche Rechnungen im Heft notiert haben!) a) 5,4 m² b) 15,5 m² |2=Tipp und Lösungen zu Nr. 16|3=Verbergen}} | ||
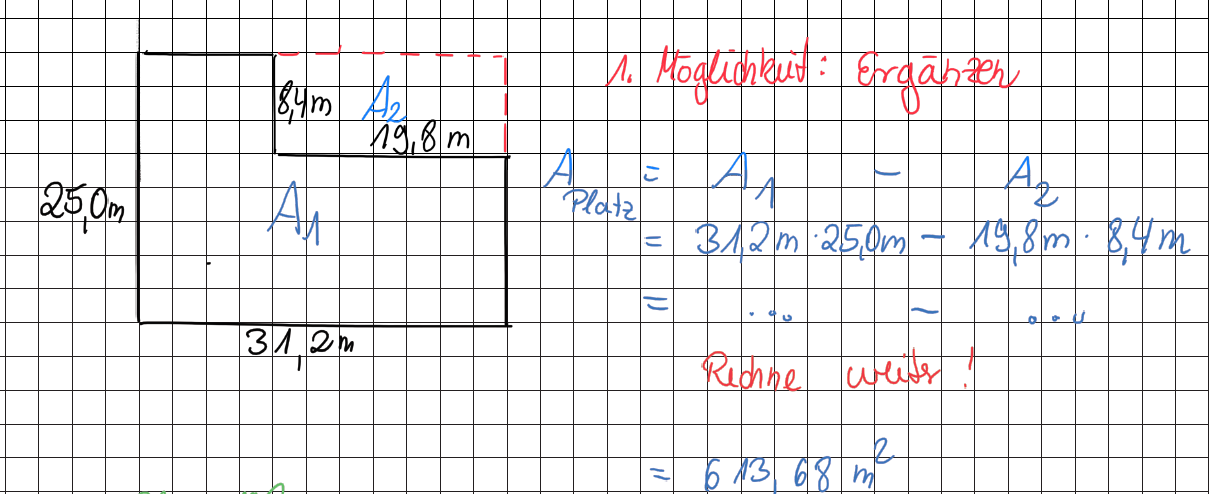
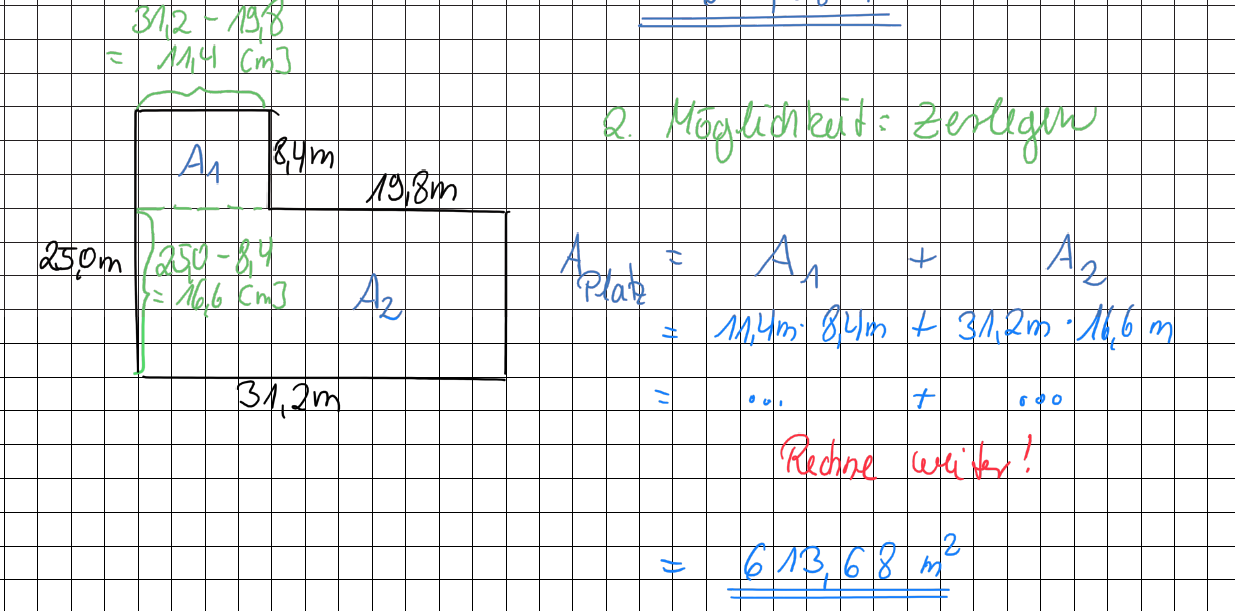
{{Lösung versteckt| Ergänze die linke Figur zu einer großen Fläche und subtrahiere dann das zu viel berechnete Rechteck| Tipp zu Nr. 17|Verbergen}} | {{Lösung versteckt| Ergänze die linke Figur zu einer großen Fläche und subtrahiere dann das zu viel berechnete Rechteck (Tipp Ergänzen) ODER zerlege die Figur in zwei Rechtecke und addiere die Flächen (Tipp Zerlegen){{Lösung versteckt|[[Datei:S. 130 Nr. 17 Tipp (Ergänzen).png]]|Tipp Ergänzen|Verbergen}}{{Lösung versteckt|[[Datei:S. 130 Nr. 17 Tipp (Zerlegen).png]]|Tipp Zerlegen|Verbergen}}| Tipps zu Nr. 17|Verbergen}} | ||
{{Lösung versteckt|1=Berechne zunächst das Volumen des Beckens (des Quaders) mit V = a · b · c , wobei c hier die Wassertiefe ist.|2=Tipp zu Nr. 21 a)|3=Verbergen}} | {{Lösung versteckt|1=Berechne zunächst das Volumen des Beckens (des Quaders) mit V = a · b · c , wobei c hier die Wassertiefe ist.|2=Tipp zu Nr. 21 a)|3=Verbergen}} | ||
Version vom 3. Mai 2020, 08:52 Uhr
2) Dezimalbrüche multiplizieren
Eine weitere Frage, die wir zu Beginn an die Weitsprungergebnisse beim Sportabzeichentag gestellt haben, war folgende:
Wenn du den besten Sprung betrachtest, wie weit kämst du dann mit 25 Sprüngen für die gesamte Klasse?
Nehmen wir noch einmal die Ergebnisse von Tom: 3m; 3,2m und 3,95m.
Die Rechnung heißt hier also: 3,95 m · 25
Um dies beantworten zu können, müssen wir Dezimalbrüche multiplizieren können. Dies lernst du auf dieser Seite.
Beginnen wir mit einer leichteren Frage:
Das kannst du sicher im Kopf berechnen. Fällt dir etwas auf?
2.1 Dezialbrüche mit 10, 100, 1000 multiplizieren
Schau das Erklärvideo on:
2.2 Dezimalbrüche multiplizieren
Wie können wir nun die Frage beantworten, wie weit die gesamte Klasse mit dem besten Sprung von Tom gesprungen wäre?
Wir müssen 3,95m · 25 rechnen.
Idee 2: Wir können Brüche multiplizieren, dies übertragen wir nun:
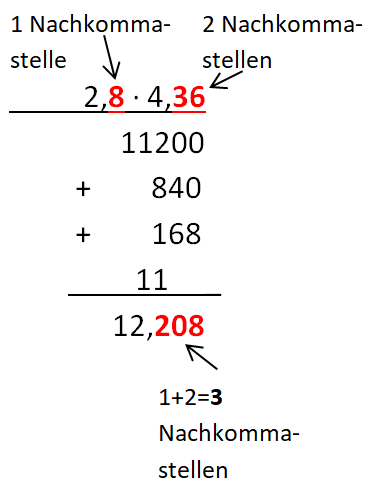
Geht das auch mit zwei Dezimalbrüchen?
Das Video fasst die Regel noch einmal zusammen:
Wo finden wir weitere Beispiele zur Multiplikation von Dezimalbrüchen im Sport?
Wir gehen schwimmen. Das Becken ist 28,5 m lang und 21,6 m breit. Welche Fläche hat der Beckenboden?
Zeichne die Skizze in dein Heft und beschrifte! Flächeninhalt eines Rechtecks A = a · b. Multipliziere schriftlich, denke an das Komma im Ergebnis.
Lösung zum Vergleichen (Du musst ausführliche Rechnungen im Heft notiert haben!) a) 5,4 m² b) 15,5 m²