Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 163: | Zeile 163: | ||
| Rechenweg anzeigen |Rechenweg verbergen}} | | Rechenweg anzeigen |Rechenweg verbergen}} | ||
'''Lösung:''' Die Wendepunkt der Funktionsscharen liegen an | '''Lösung:''' Die Rechts-links-Wendepunkt der Funktionsscharen liegen an den Punkten: <math>(\frac{a}{6}/-\frac{2}{6^3}a^3-a) </math>. | ||
| Lösung anzeigen |Lösung verbergen}} | | Lösung anzeigen |Lösung verbergen}} | ||
| Zeile 177: | Zeile 177: | ||
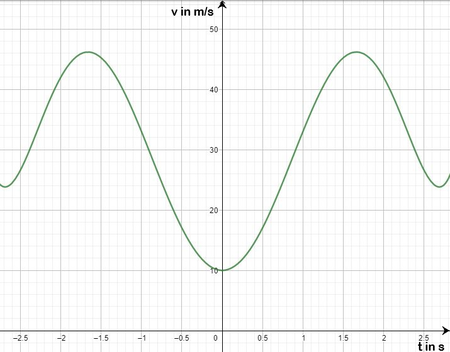
An den Stellen, wo die Achterbahn stark abbremst oder beschleunigt sind die wichtigsten Stellen der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Gebe mit Hilfe der Funktion <math> v(t) </math> an, zu welchen Zeitpunkten die Beschleunigung minimal bzw. maximal ist. | An den Stellen, wo die Achterbahn stark abbremst oder beschleunigt sind die wichtigsten Stellen der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Gebe mit Hilfe der Funktion <math> v(t) </math> an, zu welchen Zeitpunkten die Beschleunigung minimal bzw. maximal ist. | ||
{{Lösung versteckt| | {{Lösung versteckt|Die Beschleunigung <math>a(t)</math> kann man ermittel, da sie der Ableitung der Geschwindigkeit entspricht also: <math>a(t)=v'(t)</math>. Die Geschwindigkeit ist angegeben. Was gilt für die Punkte, wo die Beschleunigung maximal oder minimal ist? Lösung zu der Frage findest du in Tipp 2.| Tipp 1 anzeigen |Tipp verbergen}} | ||
{{Lösung versteckt|2| Tipp anzeigen |Tipp verbergen}} | {{Lösung versteckt|Zu dem Zeitpunkt <math>t_{W}</math> an dem die Beschleunigung maximal bzw. minimal ist gilt: <math>a'(t_{W})=0</math>, da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist. | ||
Hier muss also nur wieder der Wendepunkt berechnet werden. Falls du noch mehr Hilfe brauchst, schau dir die Tipps von Aufgabe 2 und das Beispiel nochmal an!| Tipp 2 anzeigen |Tipp verbergen}} | |||
{{Lösung versteckt|'''Rechnung:''' Notwendiges Kriterium: <math> | {{Lösung versteckt|'''Rechnung:''' Notwendiges Kriterium: <math>v(t)''(x_W)=0</math> | ||
<math>g'(x)=\frac{10x^4}{25}-3x^2+\frac{25}{8}</math> | <math>g'(x)=\frac{10x^4}{25}-3x^2+\frac{25}{8}</math> | ||