Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 24: | Zeile 24: | ||
* Berechnen des Funktionswertes durch einsetzen des Funktionstherms <math> x_W </math> in die Ursprüngliche Funktion | * Berechnen des Funktionswertes durch einsetzen des Funktionstherms <math> x_W </math> in die Ursprüngliche Funktion | ||
'''Beispiel:''' Gegeben sei die Funktion <math>f(x)=\frac{7}{12}x^4-5x^2</math> | {{Lösung versteckt|'''Beispiel:''' Gegeben sei die Funktion <math>f(x)=\frac{7}{12}x^4-5x^2</math> | ||
* Notwendiges Kriterium: <math>f''(x_W)=0</math> | * Notwendiges Kriterium: <math>f''(x_W)=0</math> | ||
<math>f'(x)=\frac{28}{12}x^3-10x</math> | <math>f'(x)=\frac{28}{12}x^3-10x</math> | ||
| Zeile 46: | Zeile 46: | ||
Und nun du... | Und nun du... | ||
| Beispiel anzeigen |Beispiel verbergen}} | |||
| Beispiel}} | | Beispiel}} | ||
| Zeile 81: | Zeile 82: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
{{Box|1= <span style="color: green"> Aufgabe 3 - Die schnelle Achterbahn</span> | {{Box|1= <span style="color: green"> Aufgabe 3 - Die schnelle Achterbahn</span> | ||
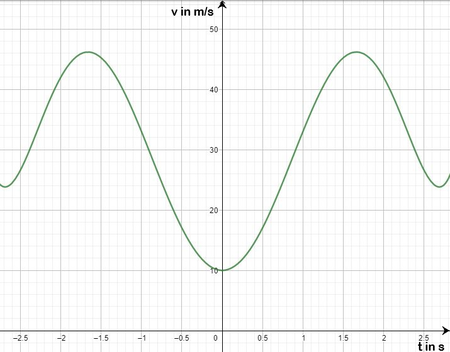
|2=Im Europa Park in Baden-Württemberg soll eine schnelle Achterbahn gebaut werden. Kurz vor Schluss soll die Bahn über zwei hohe Punkte fahren und dort die Höchstgeschwindigkeiten erreichen. Die Mitarbeiter des Parks haben eine Simulation der Achterbahn erstellt und haben somit die Geschwindigkeit der Achterbahn gegen die Zeit aufgenommen. Die Funktion <math>v(t)=\frac{1}{2}t^6-\frac{15}{2} | |2=Im Europa Park in Baden-Württemberg soll eine schnelle Achterbahn gebaut werden. Kurz vor Schluss soll die Bahn über zwei hohe Punkte fahren und dort die Höchstgeschwindigkeiten erreichen. Die Mitarbeiter des Parks haben eine Simulation der Achterbahn erstellt und haben somit die Geschwindigkeit der Achterbahn gegen die Zeit aufgenommen. Die Funktion <math>v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10</math> (siehe Abbildung) beschreibt im Intervall [-3s,3s] sehr gut die Geschwindigkeit der Achterbahn am Ende der Fahrt. | ||
[[Datei:Aufgabe Achterbahn.png|zentriert|mini|450x450px]] | [[Datei:Aufgabe Achterbahn.png|zentriert|mini|450x450px]] | ||