Benutzer:Vivien WWU-6/TestseiteAufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 101: | Zeile 101: | ||
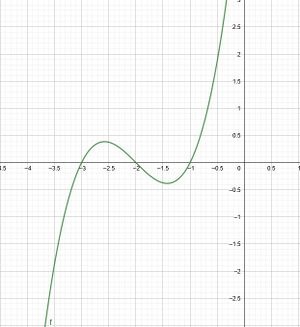
{{Lösung versteckt|1= Die Nullstellen von <math>f'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>f'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist. | {{Lösung versteckt|1= Die Nullstellen von <math>f'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>f'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist. | ||
Für <math>(-\infty, -3)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x) auf diesem Intervall streng monoton fallend. | Für <math>(-\infty, -3)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x) auf diesem Intervall streng monoton steigend. | Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend. | ||
Für <math>(-2, -1) ist <math>f'(x)<0</math>, somit ist <math>f(x) auf diesem Intervall streng monoton fallend. | Für <math>(-2, -1) ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math>(-1, +\infty)</math> Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x) auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}} | Für <math>(-1, +\infty)</math> Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}} | ||
{{Box | Aufgabe 2 | | |||
b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen <math>f(x)</math> mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft. | Arbeitsmethode}} | |||
{{Box | Aufgabe 3 | Berechne das Monotonieverhalten folgender Funktionen | Arbeitsmethode}} | {{Box | Aufgabe 3 | Berechne das Monotonieverhalten folgender Funktionen | Arbeitsmethode}} | ||
Version vom 12. April 2020, 08:57 Uhr
Monotonie
Exponentialfunktion, cosinus/sinus auf Intervallen
| Tiefpunkt |
Aus dem Ergebnis können wir schließen, dass die Funktion für streng monoton fallend und für streng monoton steigend ist.
Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen über das Monotonieverhalten liefert dir ?
Die Nullstellen von definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von verschieden ist. Nun kannst du betrachten, auf welchen Intervallen bzw. ist. Welche Aussagen kannst du damit über das Monotonieverhalten von machen?
Die Nullstellen von sind und . Damit sind die zu betrachtenden Intervalle , , und . Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob an diesen oder ist. Für ist , somit ist auf diesem Intervall streng monoton fallend. Für ist , somit ist auf diesem Intervall streng monoton steigend. Für , somit ist auf diesem Intervall streng monoton fallend.
Für Für ist , somit ist auf diesem Intervall streng monoton steigend.
| Hochpunkt | Tiefpunkt |
| Tiefpunkt |