Benutzer:Vivien WWU-6/TestseiteAufgaben

Monotonie

Merksatz

Das Monotonieverhalten einer Funktion

…beschreibt den Verlauf des Graphen einer Funktion. Sie gibt an, ob eine Funktion fällt, steigt oder konstant ist.

Sei $f(x)$ eine Funktion und $x_1<x_2$

-      Falls auf einem Intervall $f(x_1) < f(x_2)$ gilt, so ist die Funktion streng monoton steigend

-      Falls auf einem Intervall $f(x_1) \leq \ f(x_2)$ gilt, so ist die Funktion monoton steigend

-      Falls auf einem Intervall $f(x_1) > f(x_2)$ gilt, so ist die Funktion streng monoton fallend

-      Falls auf einem Intervall $f(x_1) \geq \ f(x_2)$ gilt, so ist die Funktion monoton fallend

Tipp: Du kannst leicht mithilfe der ersten Ableitung überprüfen, ob die Steigung positiv oder negativ ist!

Aufgabe 1

Ordne den Funktionen den richtigen Begriff zu

Exponentialfunktion, cosinus/sinus auf Intervallen

So berechnest du das Monotonieverhalten einer Funktion

1. Erste Ableitung berechnen

2. Nullstellen der ersten Ableitung berechnen

3. Intervalle benennen

4. Monotonietabelle aufstellen

5. Vorzeichen der Intervalle berechnen

6. Ergebnis interpretieren

Beispiel: Monotonieverhalten für $g(x)=x^2$ bestimmen

Zuerst berechnen wir die Ableitung $g'(x)=2x$. Anschließend berechnen wir die Nullstellen der Ableitung ($g'(x)=0$) und erhalten durch Umformungen als Nullstelle $x=0$. Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten $(-\infty,0)$ und $(0,+\infty)$. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle:

	$-\infty < x < 0$	$f'(0)$	$0 < x < \infty$
$f'(x)$	$< 0$	$= 0$	$> 0$
$G_{f}$	$\searrow$	Tiefpunkt	$\nearrow$

Aus dem Ergebnis können wir schließen, dass die Funktion für $(-\infty,0)$ streng monoton fallend und für $(0,+\infty)$ streng monoton steigend ist.

Aufgabe 2

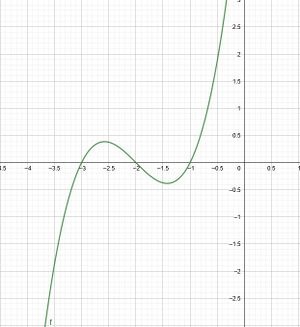
Auf dem Bild siehst du den Graphen einer Ableitungsfunktion $f'(x)$. Welche Aussagen kannst du über das Monotonieverhalten von $f(x)$ machen?

Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen über das Monotonieverhalten liefert dir $f'(x)=0$?

Die Nullstellen von $f'(x)$ definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von $f$ verschieden ist. Nun kannst du betrachten, auf welchen Intervallen $f'(x)$ $<0$ bzw. $>0$ ist. Welche Aussagen kannst du damit über das Monotonieverhalten von $f(x)$ machen?

Die Nullstellen von $f'(x)$ sind $x_1=-3, x_2=-2$ und $x_3=-1$. Damit sind die zu betrachtenden Intervalle $(-\infty, -3)$, $(-3, -2)$, $(-2, -1)$ und $(-1, +\infty)$.

Aufgabe 3

Berechne das Monotonieverhalten folgender Funktionen

	$-\infty < x < -\frac{1}{3}$	$f'\Big(-\frac{1}{3}\Big)$	$-\frac{1}{3} < x < 1$	$f'(1)$	$1 < x < \infty$
$f'(x)$	$> 0$	$= 0$	$< 0$	$= 0$	$> 0$
$G_{f}$	$\nearrow$	Hochpunkt	$\searrow$	Tiefpunkt	$\nearrow$

	$-\infty < x < 0$	$f'(0)$	$0 < x < \infty$
$f'(x)$	$< 0$	$= 0$	$> 0$
$G_{f}$	$\searrow$	Tiefpunkt	$\nearrow$