Julius-Echter-Gymnasium/Mathematik/Flächeninhalt von Dreiecken: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
K (29 Versionen importiert)
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 1: Zeile 1:
<u></u><div style="padding:50px;background: #F6CEEC;border:0px groove;">
{{Box|Dreiecke|Ein Dreieck hat drei Ecken und drei Seiten.<br />


<div style="margin:0; margin-right:50px; margin-left:50px; border:10px solid#FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
Es gibt fünf Spezialfälle von Dreiecken:|Kurzinfo}}


<colorize>Flächeninhalt von Dreiecken</colorize>


Ein Dreieck hat drei Ecken und drei Seiten.<br />
1. '''Gleichschenklige''' Dreiecke:<br />
<br />(Zwei Seiten - die beiden Schenkel - sind gleich lang. <br />Die dritte Seite - hier c - nennt man Basis.)
[[Datei:Isosceles-triangle.svg|250px|zentriert]]<br />


Es gibt drei Spezialfälle von Dreiecken:  
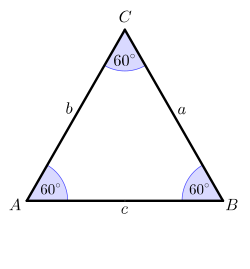
2. '''Gleichseitige''' Dreiecke: <br />
<br />(Alle 3 Seiten sind gleich lang.)
[[Datei:01-Dreieck, gleichseitig-1.svg|250px|zentriert]]<br />


1. '''Gleichschenklige''' Dreiecke (2 Seiten - die beiden Schenkel - sind gleich lang):
3. '''Rechtwinklige''' Dreiecke: <br />
[[Datei:Isosceles-triangle.svg|miniatur|zentriert]]<br />
<br />(Ein Winkel ist genau 90° groß.)
[[Datei:01-Rechtwinkliges Dreieck.svg|300px|zentriert]]<br />
<br />


2. '''Gleichseitige''' Dreiecke (alle 3 Seiten sind gleich lang):
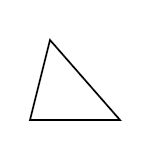
4. '''Spitzwinklige''' Dreiecke: <br />
[[Datei:01-Dreieck, gleichseitig-1.svg|miniatur|zentriert]]<br />
<br />(Alle Winkel sind kleiner als 90°.)
[[Datei:Unregelmaessiges spitzwinkliges Dreieck.png|300px|zentriert]]<br />
<br />


3. '''Rechtwinklige''' Dreiecke (ein Winkel ist 90° groß):
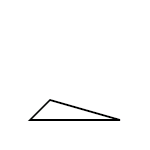
5. '''Stumpfwinklige''' Dreiecke: <br />
[[Datei:01-Rechtwinkliges Dreieck.svg|miniatur|zentriert]]<br />
<br />(Ein Winkel ist größer als 90°.<br />Dem stumpfen Winkel liegt die längste Dreiecksseite gegenüber.)
[[Datei:Unregelmaessiges stumpfwinkliges Dreieck.png|350px|zentriert]]<br />
<br />
<br />


Außerdem können Dreiecke auch '''spitzwinklig''' sein. Dann sind alle Winkel kleiner als 90° . <br />


Ein Dreieck ist '''stumpfwinklig''', wenn ein Winkel größer als 90° ist. Dem stumpfen Winkel liegt die längste Dreiecksseite gegenüber.
<br />
<br />


Die Senkrechte zwischen einer Ecke und der gegenüberliegenden Seite bezeichnet man als '''Höhe''' im Dreieck. <br />
{{Box|Höhe|Die Senkrechte zwischen einer Ecke und der gegenüberliegenden Seite bezeichnet man als '''Höhe''' im Dreieck. <br />
In jedem Dreieck gibt es drei Höhen. Diese müssen nicht unbedingt im Dreieck liegen, sie können auch außerhalb des Dreiecks verlaufen.
In jedem Dreieck gibt es drei Höhen. Diese müssen nicht unbedingt im Dreieck liegen, sie können auch außerhalb des Dreiecks verlaufen.|Unterrichtsidee }}
<br />
<br />
<br />
<br />
<br />
<br />
[[Datei:Area de paralelogramo.svg|miniatur|File:Area de paralelogramo.svg|rechts]]
[[Datei:Area de paralelogramo.svg|250px|File:Area de paralelogramo.svg]]<br />
Im Bild rechts siehst du, dass man ein Parallelogramm in zwei gleich große Dreiecke zerlegen kann. Also haben die beiden Dreiecke zusammen auch den gleichen Flächeninhalt wie das Parallelogramm. Demnach muss eins dieser Dreiecke genau halb so groß sein wie das Parallelogramm.<br />
<br />
In diesem Bild siehst du, dass man ein Parallelogramm in zwei gleich große Dreiecke zerlegen kann. <br />Also haben die beiden Dreiecke zusammen auch den gleichen Flächeninhalt wie das Parallelogramm. <br />Demnach muss eins dieser Dreiecke genau halb so groß sein wie das Parallelogramm.<br />


Für den Flächeninhalt des Dreiecks gilt deshalb: <span style="Color: red">'''A = <math> \frac{1}{2}</math> &middot; c &middot; h'''
{{Box|Merke|Den Flächeninhalt eines Dreiecks berechnest du, indem du die '''Grundseite mit der zugehörigen Höhe multiplizierst''' und dieses Produkt '''halbierst'''.|Merksatz}}
 
Die Formel lautet: <span style="Color: red">'''A = <math> \frac{1}{2}</math> &middot; a &middot; h'''
<br /><br />
<br />
<br />


Anstelle von c kannst du auch die anderen Seiten a oder b in die Formel einsetzen - hierbei ist jedoch wichtig, dass du immer die zur jeweiligen Seite senkrecht stehende Höhe verwendest.
Anstelle von a kannst du auch die anderen Dreiecksseiten b oder c in die Formel einsetzen - hierbei ist jedoch wichtig, dass du immer die '''zur jeweiligen Seite senkrecht stehende Höhe''' verwendest.
<br />
<br />
 
<br />
Dreiecke, die in einer Seitenlänge und zugehöriger Höhe übereinstimmen, besitzen auch den gleichen Flächeninhalt.
<br />
 
{{Box|Beachte|Dreiecke, die in einer Seitenlänge und zugehöriger Höhe übereinstimmen, besitzen auch den gleichen Flächeninhalt.|Kurzinfo}}




Zeile 46: Zeile 55:
Überprüfe in der ersten Übung zunächst, ob du die '''Einteilung der Dreiecke''' verstanden hast:
Überprüfe in der ersten Übung zunächst, ob du die '''Einteilung der Dreiecke''' verstanden hast:


<popup name= 1.Aufgabe>
{{Box|Aufgabe 1|{{LearningApp|app=p6bx4a2s218|width=100%|height=500px}}|Üben}}
<iframe src="https://learningapps.org/watch?v=p6bx4a2s218" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>


</popup>
<br />


In den nächsten Übungen kannst du die Formel zum Flächeninhalt von Dreiecken üben:
In den nächsten Übungen kannst du die Formel zum Flächeninhalt von Dreiecken üben:


<popup name= 2.Aufgabe>
{{Box|Aufgabe 2|{{LearningApp|app=pqnoiwcec18|width=100%|height=500px}}|Üben}}
<iframe src="https://learningapps.org/watch?v=pqnoiwcec18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>


</popup>
{{Box|Aufgabe 3|{{LearningApp|app=7235700|width=100%|height=500px}}|Üben}}
<br />


{{Box|Aufgabe 4|{{LearningApp|app=2329291|width=100%|height=500px}}|Üben}}


<popup name= 3.Aufgabe>
<iframe src="https://learningapps.org/watch?app=7235700" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>


</popup>
In der folgenden Übung werden die Flächeninhaltsformeln von Dreieck und Parallelogramm vermischt abgefragt:
<br />


{{Box|Aufgabe 5|{{LearningApp|app=7235760|width=100%|height=500px}}|Üben}}


<popup name= 4.Aufgabe>
<iframe src="https://learningapps.org/watch?app=2329291" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
</popup>
<br />
<br />




In der folgenden Übung werden die Flächeninhaltsformeln von Dreieck und Parallelogramm vermischt abgefragt:
<popup name= 5.Aufgabe>
<iframe src="https://learningapps.org/watch?app=7235760" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
</popup>
<br />


{{Fortsetzung|weiter=Flächeninhalt von Trapezen|weiterlink=Julius-Echter-Gymnasium/Mathematik/Flächeninhalt_von_Trapezen|vorher=Flächeninhalt von Parallelogrammen|vorherlink=Julius-Echter-Gymnasium/Mathematik/Flächenihnhalt_von_Parallelogrammen}}


{{Vorlage:Lesepfad Ende
{{SORTIERUNG:{{SUBPAGENAME}}}}
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Flächenihnhalt von Parallelogrammen|zurück zum Flächeninhalt von Parallelogrammen]]                  
[[Kategorie:Julius-Echter-Gymnasium Mathematik]]
|Link vor=[[Julius-Echter-Gymnasium/Mathematik/Flächeninhalt von Trapezen|Zum nächsten Thema:Flächeninhalt von Trapezen]]
|Text Copyright=
}}
<div style="padding:1px;background:#F6CEEC;border:0px groove;">

Version vom 23. Februar 2020, 11:18 Uhr

Dreiecke

Ein Dreieck hat drei Ecken und drei Seiten.

Es gibt fünf Spezialfälle von Dreiecken:


1. Gleichschenklige Dreiecke:

(Zwei Seiten - die beiden Schenkel - sind gleich lang.
Die dritte Seite - hier c - nennt man Basis.)

Isosceles-triangle.svg


2. Gleichseitige Dreiecke:

(Alle 3 Seiten sind gleich lang.)

01-Dreieck, gleichseitig-1.svg


3. Rechtwinklige Dreiecke:

(Ein Winkel ist genau 90° groß.)

01-Rechtwinkliges Dreieck.svg



4. Spitzwinklige Dreiecke:

(Alle Winkel sind kleiner als 90°.)

Unregelmaessiges spitzwinkliges Dreieck.png



5. Stumpfwinklige Dreiecke:

(Ein Winkel ist größer als 90°.
Dem stumpfen Winkel liegt die längste Dreiecksseite gegenüber.)

Unregelmaessiges stumpfwinkliges Dreieck.png






Höhe

Die Senkrechte zwischen einer Ecke und der gegenüberliegenden Seite bezeichnet man als Höhe im Dreieck.

In jedem Dreieck gibt es drei Höhen. Diese müssen nicht unbedingt im Dreieck liegen, sie können auch außerhalb des Dreiecks verlaufen.




File:Area de paralelogramo.svg

In diesem Bild siehst du, dass man ein Parallelogramm in zwei gleich große Dreiecke zerlegen kann.
Also haben die beiden Dreiecke zusammen auch den gleichen Flächeninhalt wie das Parallelogramm.
Demnach muss eins dieser Dreiecke genau halb so groß sein wie das Parallelogramm.


Merke
Den Flächeninhalt eines Dreiecks berechnest du, indem du die Grundseite mit der zugehörigen Höhe multiplizierst und dieses Produkt halbierst.

Die Formel lautet: A = · a · h


Anstelle von a kannst du auch die anderen Dreiecksseiten b oder c in die Formel einsetzen - hierbei ist jedoch wichtig, dass du immer die zur jeweiligen Seite senkrecht stehende Höhe verwendest.


Beachte
Dreiecke, die in einer Seitenlänge und zugehöriger Höhe übereinstimmen, besitzen auch den gleichen Flächeninhalt.


Überprüfe in der ersten Übung zunächst, ob du die Einteilung der Dreiecke verstanden hast:


Aufgabe 1


In den nächsten Übungen kannst du die Formel zum Flächeninhalt von Dreiecken üben:


Aufgabe 2


Aufgabe 3


Aufgabe 4


In der folgenden Übung werden die Flächeninhaltsformeln von Dreieck und Parallelogramm vermischt abgefragt:


Aufgabe 5



Flächeninhalt von Parallelogrammen
Flächeninhalt von Trapezen
Abgerufen von „https://projekte.zum.de/index.php?title=Julius-Echter-Gymnasium/Mathematik/Flächeninhalt_von_Dreiecken&oldid=15679“