Benutzer:Lena H. WWU-5/Quadratische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
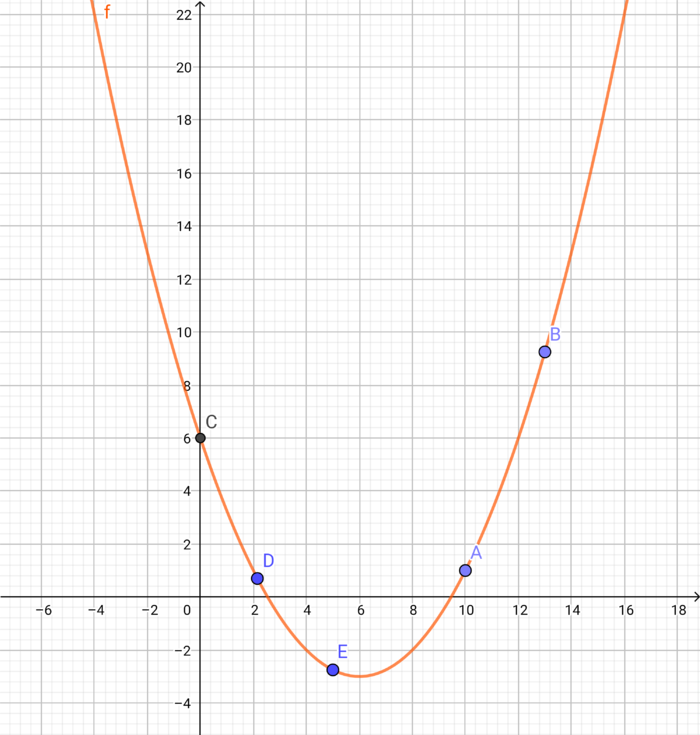
{{Box|Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen.|Gegeben sei die Funktion <math>f(x) =\frac {1} {4} \cdot (x-6)^2-3</math> und die Punkte <math> A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?) </math> und <math>E=(5|?) </math> <br /> <br /> | {{Box|3. Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen.|Gegeben sei die Funktion <math>f(x) =\frac {1} {4} \cdot (x-6)^2-3</math> und die Punkte <math> A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?) </math> und <math>E=(5|?) </math> <br /> <br /> | ||
''' a) ''' Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen. <br /><br /> | ''' a) ''' Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen. <br /><br /> | ||
{{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | {{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | ||
| Zeile 24: | Zeile 24: | ||
===Nullstellen=== | ===Nullstellen=== | ||
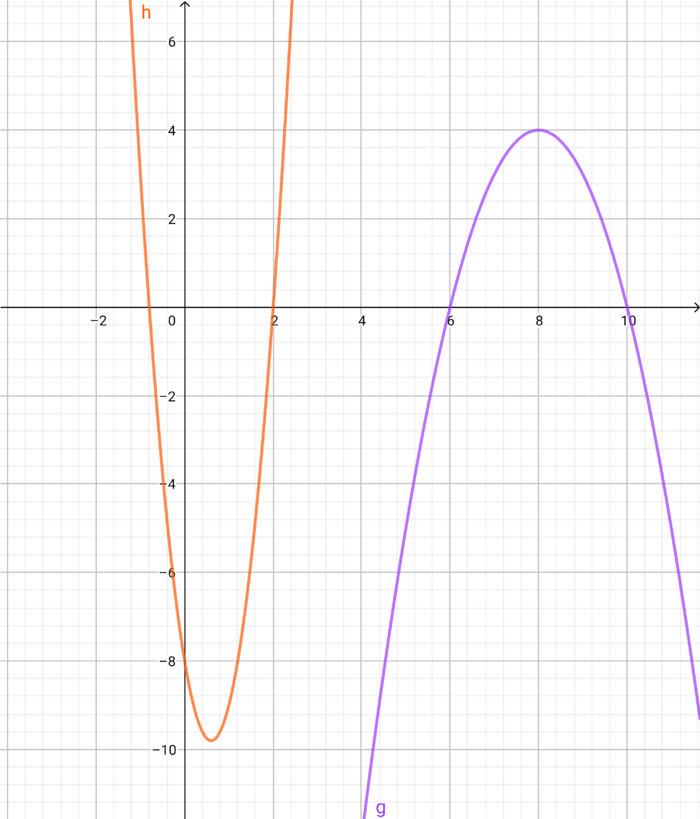
{{Box|Berechnung von Nullstellen| | {{Box|6. Berechnung von Nullstellen| | ||
Gegeben seien folgende Funktionen: <br /> | Gegeben seien folgende Funktionen: <br /> | ||
<math> g(x) = - 1 \cdot (x-8)^2+4 </math> <br /> | <math> g(x) = - 1 \cdot (x-8)^2+4 </math> <br /> | ||
| Zeile 63: | Zeile 63: | ||
Du erhälst die Gleichung <math>0 = x^2-\frac {6} {5} x-\frac{8}{5}</math><br /><br /> | Du erhälst die Gleichung <math>0 = x^2-\frac {6} {5} x-\frac{8}{5}</math><br /><br /> | ||
Durch Anwenden der pq-Formel folgt<br /><br /><br /> | Durch Anwenden der pq-Formel folgt<br /><br /><br /> | ||
<math>&\Rightarrow&x_{1} = -\frac{-\frac{6}{5}}{2}-\sqrt{\left( -\frac{\frac{6}{5}} | <math> | ||
\begin{array} {rlll} | |||
&\Rightarrow&x_{1} = -\frac{-\frac{6}{5}}{2}-\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}& \textrm{sowie}& x_{2} = -\frac{-\frac{6}{5}}{2}+\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}\\ | |||
&\Rightarrow&x_1 = 0,8& \textrm{und}& x_2 = 2\\ | |||
\end{array} | |||
</math><br /> <br /><br /> | |||
|2= Lösung zu h(x) |3=schließen}} | Arbeitsmethode}} | |2= Lösung zu h(x) |3=schließen}} | Arbeitsmethode}} | ||
{{Lösung versteckt| 1= [[Datei:Graphische Lösung zur Nullstellenberechnung.png|700px|zentriert]] |2= Graphische Lösung | 3=schließen}} | {{Lösung versteckt| 1= [[Datei:Graphische Lösung zur Nullstellenberechnung.png|700px|zentriert]] |2= Graphische Lösung | 3=schließen}} | ||