Benutzer:Stoll-Gym10Erfurt/Mathematik10/Trigonometrische Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 46: | Zeile 46: | ||
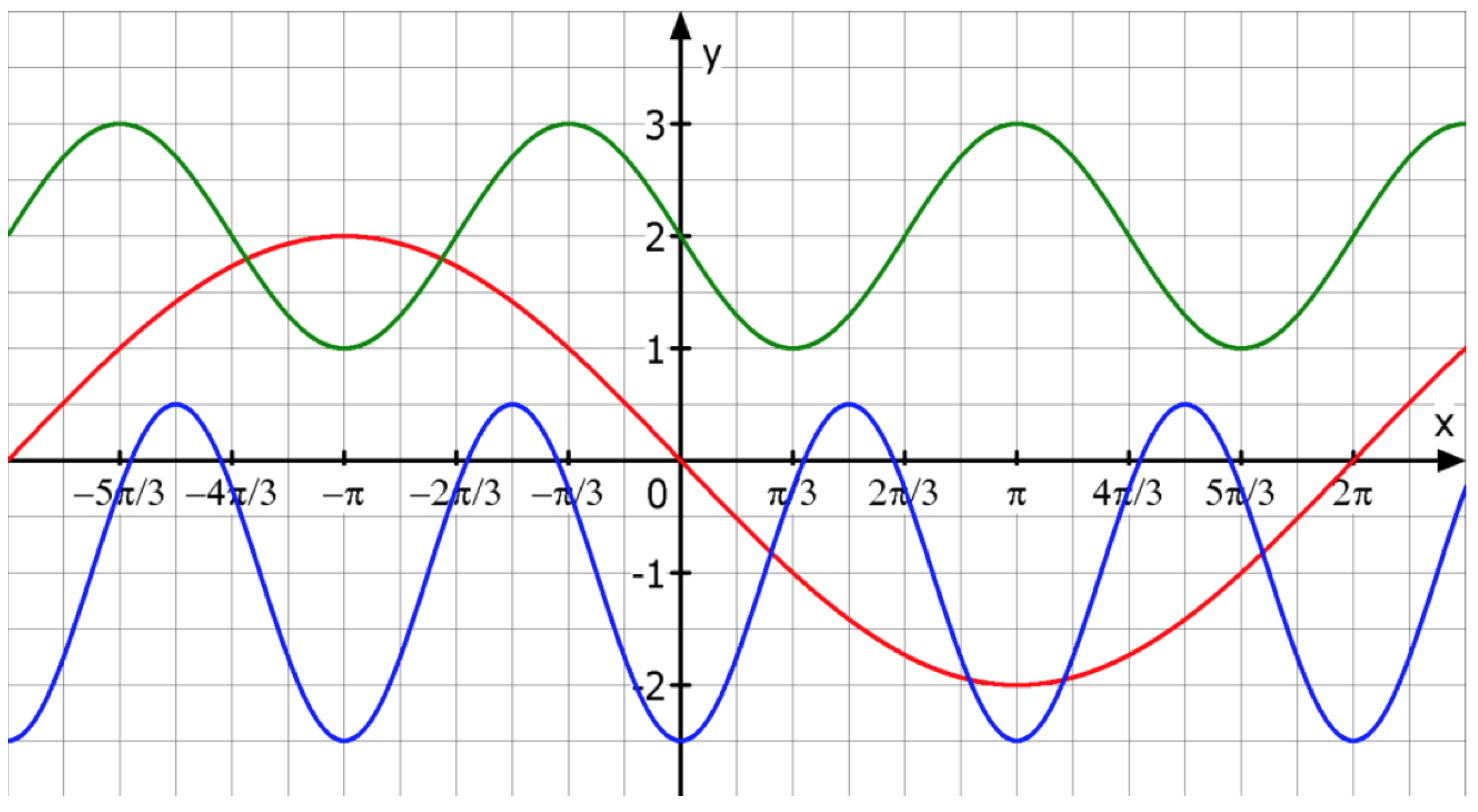
<math>f(x)=a\cdot sin(b\cdot(x-c))+d </math></big><br/> | <math>f(x)=a\cdot sin(b\cdot(x-c))+d </math></big><br/> | ||
Dabei haben die Parameter folgende Bedeutung: | Dabei haben die Parameter folgende Bedeutung: | ||
* '''a''' - Einfluss auf die Amplitude (Amplitude - Entfernung von-Achse bis zum Hoch- oder Tiefpunkt oder einfach auch "Berg- und Talspitze"). Man spricht auch von Streckung oder Stauchung in y-Richtung. | * '''a''' - Einfluss auf die Amplitude (Amplitude - Entfernung von-Achse bis zum Hoch- oder Tiefpunkt oder einfach auch "Berg- und Talspitze"). Man spricht auch von Streckung oder Stauchung in y-Richtung. Wenn a < 0 erfolgt eine Spiegelung an der x-Achse. | ||
* '''b''' - Veränderung der Periode p (Periode - Eine komplette Auf- und Abwärtsbewegung oder Abstand zwischen zwei Bergspitzen) | * '''b''' - Veränderung der Periode p (Periode - Eine komplette Auf- und Abwärtsbewegung oder Abstand zwischen zwei Bergspitzen) | ||
<math>\qquad</math> Es gilt folgende Gleichung: <math>p=\frac{2\pi}{b} </math>.<br/> | <math>\qquad</math> Es gilt folgende Gleichung für die Periode: <math>p=\frac{2\pi}{b} </math>.<br/> | ||
<math>\qquad</math> Somit ergeben sich folgende Zusammenhänge: <math>b=1 \rightarrow p=2\pi, b=2 \rightarrow p=\pi, b=4 \rightarrow p=\frac{\pi}{2} </math> | <math>\qquad</math> Somit ergeben sich folgende Zusammenhänge: <math>b=1 \rightarrow p=2\pi, b=2 \rightarrow p=\pi, b=4 \rightarrow p=\frac{\pi}{2} </math> | ||
* '''c''' - Verschiebung in x-Richtung; c > 0 nach rechts, c < 0 nach links | * '''c''' - Verschiebung in x-Richtung; c > 0 nach rechts, c < 0 nach links | ||