Benutzer:Buss-Haskert/Rationale Zahlen 7E: Unterschied zwischen den Versionen
(Bild ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
(Navigation) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation|[[Benutzer:Buss-Haskert/Rationale Zahlen 7E/Menge Z| 1. Menge ℤ]]<br> | |||
[[Benutzer:Buss-Haskert/Rationale Zahlen 7E/Menge Z|2. Temperatur]]<br> | |||
[[Benutzer:Buss-Haskert/Rationale Zahlen 7E/Thermometer|3. Thermometer]]<br> | |||
[[Benutzer:Buss-Haskert/Rationale Zahlen 7E/Zahlengerade|4. Zahlengerade]]<br> | |||
[[Benutzer:Buss-Haskert/Rationale Zahlen 7E/Zahlen vergleichen|5. Zahlen vergleichen und ordnen]]}} | |||
=== 1. Menge ℤ === | === 1. Menge ℤ === | ||
Version vom 23. März 2025, 09:51 Uhr
1. Menge ℤ
Die Anfangs- und Endbuchstaben geben dir Hinweise auf die gesuchten Wörter
T_ _ _ _ _ _ _ _ R
K _ _ _ _ _ _ _ _ D
F _ _ _ _ _ _ _ L

Originallink https://www.geogebra.org/m/g7vn8g7u

Originallink https://www.geogebra.org/m/bymavnud

Applet des FLINK-Teams
2. Temperatur
Originallink https://www.geogebra.org/m/bawhmrb4

Applet des FLINK Teams
Originallink https://www.geogebra.org/m/jfgfsxqz

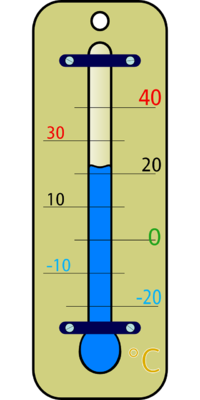
3. Thermometer
4. Zahlengerade und Zahlen ordnen
Originallink


Originallink https://www.geogebra.org/m/qquy2baz

Originallink https://www.geogebra.org/m/vr4zkpjd

Originallink https://www.geogebra.org/m/twnbuzxp

Positive und negative Zahlen können wir an der Zahlengeraden darstellen:
Die negativen Zahlen liegen links von der Null.
Die positiven Zahlen liegen rechts von der Null.
Die Null liegt in der Mitte.
5. Zahlen ordnen
Habt ihr vielleicht so argumentiert? -4°C eine niedrigere Temperatur ist als -1°C, -4€ ein niedrigerer Kontostand als -1€ und -4m tiefer unter dem Meeresspiegel ist als -1m. Auf der Zahlengeraden sind die Zahlen kleiner, je weiter links sie liegen, so wie das auch bei den positiven Zahlen ist.
Die Vorstellungen zu den negativen Zahlen helfen dir auch beim Ordnen und Vergleichen der Zahlen. Fülle die Lücken passend:
a) 36 € ist mehr als -36 €
b) 15 m ist höher als -17 m
c) -2500 € ist weniger als 10€
d) -9 m ist unterhalb von 0 m
e) -5°C ist wärmer als -12°C
f) -8°C ist kälter als 6°C
Kleiner- und Größer-Zeichen Merke dir: Das Krokodil Kroko hat immer einen riesigen Hunger. Deshalb reißt es sein Maul weit auf und schnappt nach der größeren "Beute", hier der größeren Zahl.
Nutze das GeoGebra-Applet als Hilfe, indem du die Zahlen jeweils auf der Zahlengeraden einstellst.

(von solero education)
a) 5 > -5
b) 3 > -6
c) -5 < 2
d) -9 < 0
e) -5 > -12
f) -8 < -6
Originallink https://www.geogebra.org/m/gyhssnhd

Originallink https://www.geogebra.org/m/qfbrjymr

Originallink https://www.geogebra.org/m/bwhnfurg (Hier musst du den Originallink anklicken!)

Originallink https://www.geogebra.org/m/x4e8jmxt

Applets des FLINK Teams
Vergleiche deine Lösungen (Bunte Mischung)
Vergleiche deine Lösungen (Bunte Mischung)
Tipp zum Zeichnen der Temperaturskala:
Übungen im Arbeitsheft
Zu AH, Nr. 1 Originallink https://www.geogebra.org/m/eqbsz8ce

Originallink https://www.geogebra.org/m/ujpqgvdf

Applets des FLINK Teams
Zu AH, Nr. 2 (Parkhaus)
Originallink https://www.geogebra.org/m/ufwzs9u3

Applet des FLINK Teams
Zu AH, Nr. 3 (Meereshöhen) Originallink https://www.geogebra.org/m/nugf28js

Originallink https://www.geogebra.org/m/htgp4zcr

Applets des FLINK Teams