Benutzer:Buss-Haskert/Daten/Daten auswerten

zurück zur Seite der Herta-Lebenstein-Realschule

Vorwissen

3) Daten auswerten (Kennwerte)

4) Daten darstellen (Boxplots)

Statistik-Projekt: "Wie viele YouTube-Videos schauen wir?"

Hier ist eine spannende Auswertung einer Befragung in der Klasse 8d zum YouTube-Konsum (Videos pro Tag):

Erhobene Daten (27 Schüler/innen):
3, 8, 12, 4, 15, 6, 5, 10, 7, 20, 4, 8, 6, 9, 11, 5, 7, 13, 7, 6, 3, 7, 4, 18, 13, 14, 10
Beantworte die folgenden Fragen:
a) Wie viele Videos wurden mininal geschaut?
b) Wie viele Videos wurden maximal geschaut?
c) Wie viele Videos schauten die Hälfte aller Schülerinnen und Schüler?
d) Wie viele Videos wurden von einem Viertel der Schülerinnen und Schüler geschaut?
e) Wie viele Videos wurden von drei Viertel der Schülerinnen und Schüler geschaut?
f) Wie viele Videos wurden durchschnittlich geschaut?
g) Wie groß ist die Spannweite?

h) Wie viele Videos schaut die Klasse pro Woche?

Sortiere zunächst die Werte der Größe nach. Dies heißt Rangliste:

Rang	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.	17.	18.	19.	20.	21.	22.	23.	24.	25.	26.	27.
Wert	3	3	4	4	4	5	5	6	6	6	7	7	7	7	8	8	9	10	10	11	12	13	13	14	15	18	20

oder kurz: 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 10, 10, 11, 12, 13, 13, 14, 15, 18, 20

Diese Fragen gehören zu sogenannten 📊 Statistischen Kennwerten:

Kennwert	Rang	Wert	Bedeutung
Minimum	1	3	kleinster Wert der Rangliste
Maximum	27	20	größter Wert der Rangliste
Zentralwert (Median)	$\tfrac{1}{2}$·27=13,5 ≈14 (immer aufrunden)	7	Wert in der Mitte der Rangliste
unteres Quartil (1. Quartil)	$\tfrac{1}{4}$·27 = 6,75 ≈ 7 (immer aufrunden)	5	Wert der Rangliste, der die untere Hälfte in zwei Hälften teilt
oberes Quartil (3. Quartil)	$\tfrac{3}{4}$·27 = 20,25 ≈21 (immer aufrunden)	12	Wert der Rangliste, der die oberer Hälfte in zwei Hälften teilt
arithmetisches Mittel	unabhängig vom Rang	$\bar{a} = \tfrac{3+3+4+4+4+...+13+14+15+18+20}{27} =\tfrac{241}{27}$ ≈ 8,926	Durchschnitt
Spannweite	unabhängig vom Rang	20-3 = 17	Differenz zwischen Maximum und Minimum

📈 Interpretation für die Klasse

a) Am wenigsten wurden 3 Videos geschaut.
b) Maximal wurden 20 Videos geschaut.
c) Die Hälfte (50% der Klasse) schaut mehr, die andere weniger als 7 Videos.
d) 25% schauen weniger als 5 Videos .
e) 75% schauen weniger als 12 Videos
Die meisten (50% der Klasse) schauen also zwischen 5 und 12 Videos täglich.
f) Durchschnittlich schauen alle ca. 9 Videos/Tag
g) Die Spannweite ist sehr groß: Von 3 bis 20 Videos, also 17!

h) Pro Woche kommt die Klasse auf etwa 1700 Videos 😮.

🤔 Diskussionsfragen für die Klasse

1. Ist euer YouTube-Konsum zu hoch?
2. Welche Arten von Videos schaut ihr am liebsten?
3. Wie könnt ihr eure Zeit auf YouTube sinnvoll einteilen?

Tipp: Mit euren Smartphones könnt ihr in den YouTube-Einstellungen nachsehen, wie viele Videos ihr wirklich pro Tag schaut!

Kennst du wichtige Begriffe? Teste dich:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Statistik Projekt: Handy-Screen-Time pro Tag

Hier ist eine spannende Auswertung einer Befragung in der Klasse 8e zur Handy-Screen-Time pro Tag:

Erhobene Daten in einer Rangliste sortiert(28 Schüler/innen):
1,5; 2,0; 2,0; 2,5; 2,5; 2,5; 3,0; 3,0; 3,0; 3,5; 3,5; 3,5; 4,0; 4,0; 4,0; 4,0; 4,5; 4,5; 5,0; 5,0; 5,5; 5,5; 6,0; 6,0; 6,5; 7,0; 7,5; 8,0
Werte die statistischen Kenngrößen 📊 aus und interpretiere sie für die Klasse.

Rang	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.	17.	18.	19.	20.	21.	22.	23.	24.	25.	26.	27.	28.
Wert	1,5	2,0	2,0	2,5	2,5	2,5	2,5	3,0	3,0	3,0	3,5	3,5	3,5	4,0	4,0	4,0	4,0	4,5	4,5	5,0	5,0	5,5	5,5	6,0	6,0	6,5	7,0	8,0

Kennwert	Rang	Wert
Minimum	1	1,5
Maximum	28	8
Zentralwert (Median)	$\tfrac{1}{2}$·28=14 also Mittelwert des 14. und 15. Ranges	$\tfrac{4,0+4,0}{2}$=4,0
unteres Quartil (1. Quartil)	$\tfrac{1}{4}$·28 = 7 also Mittelwert des 7. und 8. Ranges	$\tfrac{2,5+3,0}{2}$=2,75
oberes Quartil (3. Quartil)	$\tfrac{3}{4}$·28 = 21 also Mittelwert des 21. und 22. Ranges	$\tfrac{5,0+5,5}{2}$=5,25
arithmetisches Mittel	unabhängig vom Rang	$\bar{a} = \tfrac{1,5+2,0+2,0+...+7,0+8,0}{28} =\tfrac{119,5}{28}$ ≈ 4,27
Spannweite	unabhängig vom Rang	8,0 - 1,5 = 6,5

Tabelle der eigenen Umfrage: Handy-Screenzeit

Rang	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.	16.	17.	18.	19.	20.	21.
Wert	0	0	1,0	1,0	1,5	2,0	2,5	2,5	2,5	3,0	3,0	3,0	3,5	3,5	3,5	3,5	4,0	4,0	4,5	5,0	6,5

Kennwert	Rang	Wert
Minimum	1
Maximum	21
Zentralwert (Median)	$\tfrac{1}{2}$·21=10,5 also 11. Rang
unteres Quartil (1. Quartil)	$\tfrac{1}{4}$·21 = 5,25 also 6. Rang
oberes Quartil (3. Quartil)	$\tfrac{3}{4}$·21 = 15,75 also 16. Rang
arithmetisches Mittel	unabhängig vom Rang	$\bar{a} = \tfrac{0+0+1,0+...+5,0+6,5}{21} =...$ ≈ ...
Spannweite	unabhängig vom Rang

📈 Interpretation für die Klasse

a) Am wenigsten wurde 1,5 Stunde das Handy genutzt.
b) Maximal wurden 8 Stunden am Handy verbracht.
c) Die Hälfte (50% der Klasse) nutzen ihr Handy mehr, die andere weniger als 4 Stunden.
d) 25% nutzen es weniger als 2,75 Stunden.
e) 75% nutzen es weniger als 5,25 Stunden.
Die meisten (50% der Klasse) nutzen ihr Handy also zwischen 2,75 und 5,25 Stunden täglich.
f) Durchschnittlich nutzen alle ca. 4,27 Stunden täglich ihr Smartphone.
g) Die Spannweite ist sehr groß: Von 1,5 bis 8 Stunden täglich, also 6,5 Stunden!

Vergleich mit Empfehlungen

Experten empfehlen maximal 2 Stunden Handyzeit pro Tag.
Nur 5 Schüler/innen (18%) bleiben unter dieser Empfehlung.
Möchtest du dir persönliche Ziele setzen?

• Bildschirmzeit für 30 Minuten pro Tag reduzieren.
• Eine "handyfreie" Stunde vor dem Schlafengehen
• Apps mit Zeitlimits versehen

Tabelle der eigenen Umfrage Zeit an der Spielekonsole

Rang	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.
Wert	0,5	1	1,5	2,0	2,0	2,0	3,0	3,0	3,0	3,5	4,0	5,5	6

Kennwert	Rang	Wert
Minimum	1
Maximum	13
Zentralwert (Median)	$\tfrac{1}{2}$·13=... also ... Rang
unteres Quartil (1. Quartil)	$\tfrac{1}{4}$·13 = ... also ... Rang
oberes Quartil (3. Quartil)	$\tfrac{3}{4}$·13 = ... also ... Rang
arithmetisches Mittel	unabhängig vom Rang	$\bar{a} = \tfrac{1+1,5+...+5,5+6,5}{21} =...$ ≈ ...
Spannweite	unabhängig vom Rang

Flohsprung

Wir führen das Experiment FLOHSPRUNG durch:

Arbeitet in euren Tischgruppen zusammen: Material:

• 2 Plättchen pro Person
• 1 Maßband
• zwei lang hintereinander gestellte Tische

Spiel: Ein Partner darf 15-mal seinen „Floh“ springen lassen, der andere 18-mal. Die Weite jedes Sprunges wird gemessen und von den Partnern notiert. Ergänze am Ende des Spiels deine Werte auf deinem AB. (ALLE schreiben also ALLES auf)

Datei:AB Daten Flohsprung.pdf

Frage zur Auswerung in der Gruppe

• Wer ist am besten im "Flohsprung"?
• Wer hat gleichbleibend gute Werte?
• Wie weit kommt der schlechteste Sprung maximal?
• Wie weit kommt der beste Sprung?
• Vergleich die Mittelwerte der Flohsprünge.

Übung 1

Löse auf der Seite Aufgabenfuchs die nachfolgenden Aufgaben:
Urliste, Rangliste, Kennwerte (Minimum, Maximum, Zentralwert, Spannweite, Mittelwert):

• Nr. 1 bis Nr. 9

Relative Häufigkeit

• Nr. 10 bis 23

Nun noch einmal die obige Aufgabe:

Frage zur Auswerung in der Gruppe

• Wer ist am besten im "Flohsprung"?
• Wer hat gleichbleibend gute Werte?
• Wie weit kommt der schlechteste Sprung maximal?
• Wie weit kommt der beste Sprung?
• Vergleich die Mittelwerte der Flohsprünge.

Als Beispiel findest du hier die Werte von Tim und Tina.

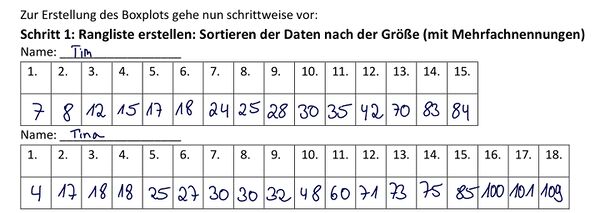
• schlechtester Sprung (Minimum): Tim 7 cm; Tina 4 cm
  
• bester Sprung (Maximum): Tim: 84 cm; Tina 109 cm
  
• Mittelwerte (arithmetisches Mittel):
  

Tim: $\bar{a} = \tfrac{7+8+12+15+17+18+24+25+28+30+35+42+70+83+84}{15} =\tfrac{498}{15} = 33,2 (cm)$
Tina: $\bar{a} = \tfrac{4+17+18+18+25+27+30+30+32+48+60+71+73+75+85+100+101+109}{18} =\tfrac{923}{18} = 51,3 (cm)$

• Median (Zentralwert):
  

Tim Rang: $\tfrac{15}{2}$ = 7,5, also Rang 8: 25 cm

Tina Rang: $\tfrac{18}{2}$ = 9, also Mittelwert des 9. und 10. Ranges: $\tfrac{32+48}{2} = \tfrac{80}{2} = 40 (cm)$

Um diese Daten auszuwerten, helfen die dir schon bekannten Kennwerte:

Kennwerte

Kennwert	Beschreibung
Minimum	Der kleinste Wert der Rangliste heißt Minimum.
Maximum	Der größte Wert der Rangliste heißt Maximum.
Spannweite	Die Differenz aus dem Maximum und dem Minimum heißt Spannweite.
Zentralwert/Median	Der Wert in der Mitte einer Rangliste heißt Median bzw. Zentralwert.
Quartil	Die Quartile teilen die Rangliste in vier Abschnitte. In jedem dieser Abschnitte befinden sich 25% der Werte.
unteres Quartil	Der Wert der Rangliste, der die untere Hälfte in zwei Hälften teilt, heißt unteres Quartil (also der Median der unteren Datenhälfte).
oberes Quartil	Der Wert der Rangliste, der die obere Hälfte in zwei Hälften teilt, heißt oberes Quartil (also der Median der oberen Datenhälfte).

Übung 2

Löse auf der Seite Aufgabenfuchs die nachfolgenden Aufgaben:
Bestimmung der Quartile: (Lies zunächst die Information vor Nr. 26.)

• Nr. 26 und Nr. 27

Das Video erklärt dir, wie du die erhobenen Daten mit einem Boxplot darstellen kannst. Die Anzahl der Daten ist hier ungerade.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Das nächste Video erklärt dies noch einmal, hier ist der Sonderfall, dass die Anzahl der Daten gerade ist. Die Bestimmung des Zentralwertes und der Quartile erfolgt hier leicht abgeändert:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 3

Löse auf der Seite Aufgabenfuchs die nachfolgenden Aufgaben:
Boxplot:

• Nr. 29 bis Nr. 32

Erstelle nun eine Rangliste der geworfenen Weiten und ermittle anhand dieser Rangliste die Kennwerte Minimum, unteres Quartil, Median, oberes Quartil, Maximum.

4) Daten darstellen (Boxplots)