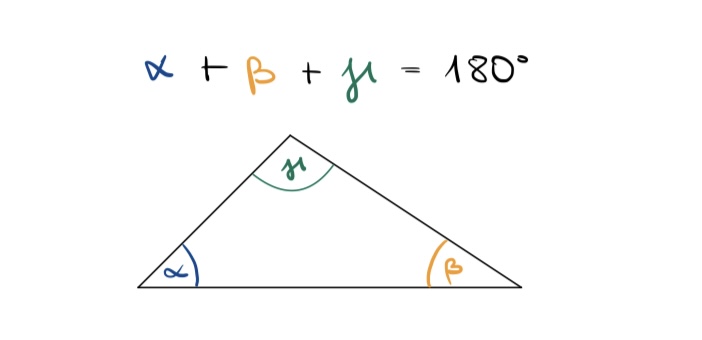Geometrie im Dreieck/Geheimcode der Geometrie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 31: | Zeile 31: | ||
|3=Definition}} | |3=Definition}} | ||
== Aufgabe 1 == | == Aufgabe 1 == | ||
{{Box | | {{Box | Aufgabe 1.1:Grundlagen - Berechnung eines Winkels im Dreieck |Ein Dreieck hat die Winkel | ||
50° und 60°. Berechne den fehlenden Winkel und überprüfe, ob die Innenwinkelsumme des Dreiecks 180° ergibt. | Arbeitsmethode | Farbe={{Farbe|orange}}}} | 50° und 60°. Berechne den fehlenden Winkel und überprüfe, ob die Innenwinkelsumme des Dreiecks 180° ergibt. | Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
{{Lösung versteckt|1='''Tipps:''' | {{Lösung versteckt|1='''Tipps:''' | ||
| Zeile 43: | Zeile 43: | ||
Fehlender Winkel: 70°. | Fehlender Winkel: 70°. | ||
|2=Lösung|3=Lösung verbergen}} | |2=Lösung|3=Lösung verbergen}} | ||
{{Box | | {{Box | Aufgabe 1.2:Kombination von Innenwinkelsumme und Stufenwinkel |Ein Dreieck liegt zwischen zwei parallelen Linien. Ein Außenwinkel des Dreiecks beträgt 120°, und ein Innenwinkel beträgt 40°. | ||
Ein Dreieck liegt zwischen zwei parallelen Linien. Ein Außenwinkel des Dreiecks beträgt 120°, und ein Innenwinkel beträgt 40°. | |||
# Berechne den zweiten Innenwinkel des Dreiecks mit Hilfe der Stufenwinkel-Regel. | # Berechne den zweiten Innenwinkel des Dreiecks mit Hilfe der Stufenwinkel-Regel. | ||
| Zeile 58: | Zeile 57: | ||
** Fehlender Winkel b: 40°+60°+b=180° b=180°−40°−60°=80° | ** Fehlender Winkel b: 40°+60°+b=180° b=180°−40°−60°=80° | ||
* '''Zeichnung:''' Zeichne zwei parallele Linien, ein Dreieck dazwischen und markiere die Winkel 40°,60°,80° .|2=Lösung|3=Lösung verbergen}} | * '''Zeichnung:''' Zeichne zwei parallele Linien, ein Dreieck dazwischen und markiere die Winkel 40°,60°,80° .|2=Lösung|3=Lösung verbergen}} | ||
{{Box | Wechselwinkel und mehrere Dreiecke |Zwei Dreiecke liegen nebeneinander und teilen eine gemeinsame Seite. Die beiden Dreiecke befinden sich zwischen zwei parallelen Linien. Im ersten Dreieck beträgt ein Innenwinkel 70°, und der Außenwinkel an der gemeinsamen Seite beträgt 110°. | {{Box | Aufgabe 1.3 Wechselwinkel und mehrere Dreiecke |Zwei Dreiecke liegen nebeneinander und teilen eine gemeinsame Seite. Die beiden Dreiecke befinden sich zwischen zwei parallelen Linien. Im ersten Dreieck beträgt ein Innenwinkel 70°, und der Außenwinkel an der gemeinsamen Seite beträgt 110°. | ||
Im zweiten Dreieck beträgt ein Innenwinkel 50°, und ein anderer Innenwinkel ist ein Wechselwinkel des Außenwinkels des ersten Dreiecks. | Im zweiten Dreieck beträgt ein Innenwinkel 50°, und ein anderer Innenwinkel ist ein Wechselwinkel des Außenwinkels des ersten Dreiecks. | ||
Berechne alle fehlenden Winkel in beiden Dreiecken. | Berechne alle fehlenden Winkel in beiden Dreiecken. | ||
Version vom 10. Dezember 2024, 09:18 Uhr
Informationskästchen
Die Innenwinkelsumme im Dreieck
Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht
Aufgabe 1
Tipps:
- Die Innenwinkelsumme eines Dreiecks beträgt immer 180°.
- Addiere die beiden gegebenen Winkel.
- Subtrahiere die Summe von 180°, um den fehlenden Winkel zu berechnen.
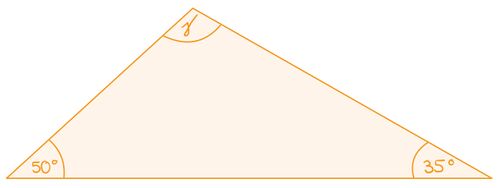
Gegebene Winkel: 50°, 60°. Berechnung: 50°+60°+x=180° x=180°−50°−60°=70°
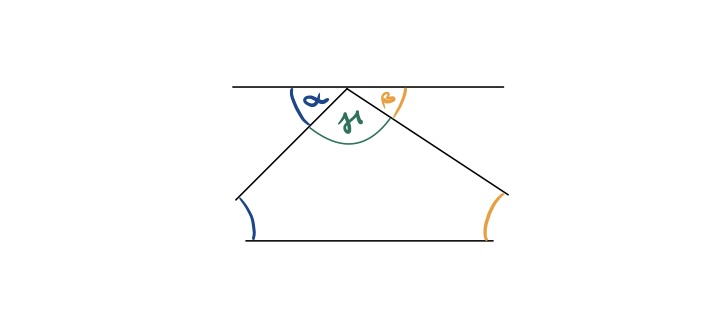
Fehlender Winkel: 70°.- Nutze die Stufenwinkel-Regel: Wenn zwei Linien parallel sind, sind die Stufenwinkel gleich.
- Berechne den zweiten Innenwinkel mithilfe der Stufenwinkel.
- Verwende die Innenwinkelsumme, um den dritten Winkel zu berechnen.
- Berechnung des zweiten Innenwinkels:
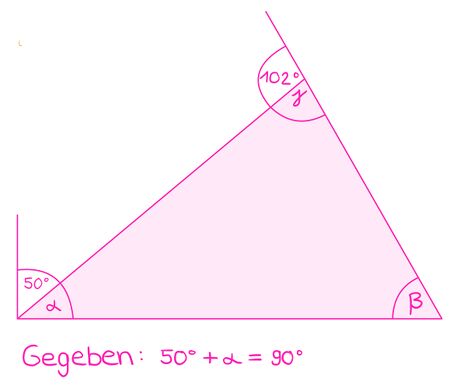
- Der Außenwinkel 120° liegt an einer der parallelen Linien. Sein zugehöriger Innenwinkel a ist ein Nebenwinkel: a=180°−120°=60°
- Berechnung des dritten Innenwinkels:
- Gegebene Winkel: 40° und 60°.
- Fehlender Winkel b: 40°+60°+b=180° b=180°−40°−60°=80°
- Zeichnung: Zeichne zwei parallele Linien, ein Dreieck dazwischen und markiere die Winkel 40°,60°,80° .
- Nutze die Wechselwinkel-Regel: Wechselwinkel sind gleich, wenn zwei Linien parallel sind.
- Berechne zunächst den fehlenden Winkel des ersten Dreiecks mithilfe der Nebenwinkel-Regel.
- Nutze den Wechselwinkel, um den fehlenden Winkel im zweiten Dreieck zu bestimmen.
- Erstes Dreieck:
- Gegebene Winkel: 70° und ein Außenwinkel 110°.
- Der Innenwinkel an der gemeinsamen Seite: a=180°−110°=70°
- Fehlender Winkel b: 70°+70°+b=180° b=180°−70°−70°=40°
- Zweites Dreieck:
- Ein Innenwinkel ist ein Wechselwinkel des Außenwinkels 110° des ersten Dreiecks: a=110°
- Gegebener Winkel: 50°.
- Fehlender Winkel c: 50°+110°+c=180° c=180°−50°−110°=20°
- Überprüfung der Innenwinkelsummen:
- Erstes Dreieck: 70°+70°+40°=180°.
- Zweites Dreieck: 50°+110°+20°=180°.
Aufgabe 2
Aufgabe 3
Hier kommst du zurück zur Startseite des Kapitels: Geometrie im Dreieck