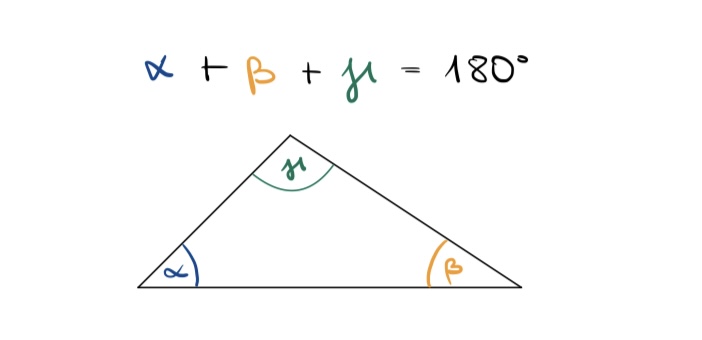Geometrie im Dreieck/Geheimcode der Geometrie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 28: | Zeile 28: | ||
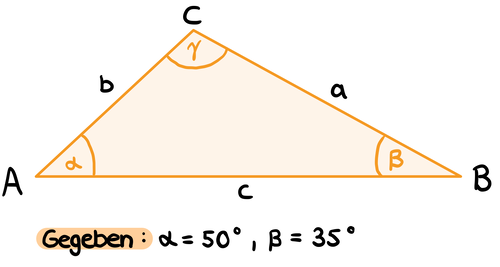
{{Lösung versteckt|1=Berechne den fehlenden Winkel γ, indem du die Winkel α und β von 180° abziehst.|2=Tipp|3=Tipp verbergen}} | {{Lösung versteckt|1=Berechne den fehlenden Winkel γ, indem du die Winkel α und β von 180° abziehst.|2=Tipp|3=Tipp verbergen}} | ||
{{Lösung versteckt|1=[[Datei:Lösung 2.1 orange.png|zentriert|rahmenlos|500x500px]]|2=Lösung|3=Lösung verbergen}}| Arbeitsmethode | Farbe={{Farbe|orange}}}} | {{Lösung versteckt|1=[[Datei:Lösung 2.1 orange.png|zentriert|rahmenlos|500x500px]]|2=Lösung|3=Lösung verbergen}}| Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
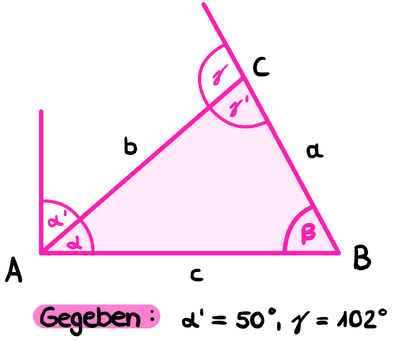
{{Box | Aufgabe 2.2|Erkenne die Innenwinkel und berechne sie! | {{Box | Aufgabe 2.2|Erkenne die Innenwinkel des Dreiecks und berechne sie! | ||
[[Datei:Aufgabe 2.2 pink.png|zentriert|rahmenlos|400x400px]] | [[Datei:Aufgabe 2.2 pink.png|zentriert|rahmenlos|400x400px]] | ||
{{Lösung versteckt|1=α und α' bilden einen rechten Winkel. Es gilt also α+α'=90°. Wie kannst du herausfinden, wie groß α ist?|2=Tipp 1|3=Tipp1 verbergen}} | {{Lösung versteckt|1=α und α' bilden einen rechten Winkel. Es gilt also α+α'=90°. Wie kannst du herausfinden, wie groß α ist?|2=Tipp 1|3=Tipp1 verbergen}} | ||
| Zeile 34: | Zeile 34: | ||
{{Lösung versteckt|1=Berechne den fehlenden Winkel β mithilfe des Innenwinkelsatzes!|2=Tipp 3|3=Tipp 3 verbergen}} | {{Lösung versteckt|1=Berechne den fehlenden Winkel β mithilfe des Innenwinkelsatzes!|2=Tipp 3|3=Tipp 3 verbergen}} | ||
{{Lösung versteckt|1=[[Datei:Lösung 2.2 pink.png|zentriert|rahmenlos|800x800px]]|2=Lösung|3=Lösung verbergen}}| Arbeitsmethode | Farbe=#CD2990 }} | {{Lösung versteckt|1=[[Datei:Lösung 2.2 pink.png|zentriert|rahmenlos|800x800px]]|2=Lösung|3=Lösung verbergen}}| Arbeitsmethode | Farbe=#CD2990 }} | ||
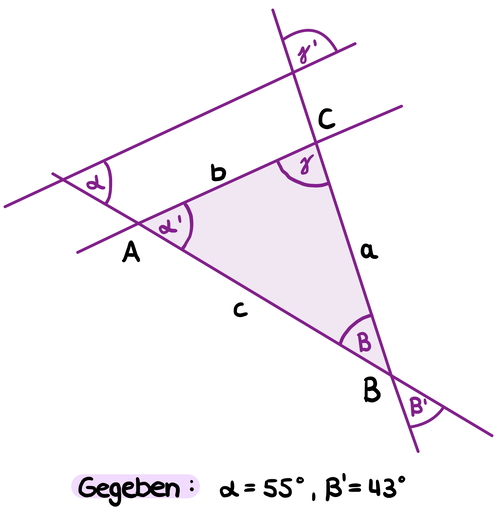
{{Box | Aufgabe 2.3|Bestimme die Innenwinkel! | {{Box | Aufgabe 2.3|Bestimme die Innenwinkel des Dreiecks! | ||
[[Datei:Aufgabe 2.3 lilaaa.png|zentriert|rahmenlos|509x509px]] | [[Datei:Aufgabe 2.3 lilaaa.png|zentriert|rahmenlos|509x509px]] | ||
{{Lösung versteckt|1=α und α' sind Stufenwinkel. Wie groß ist dann α'?|2=Tipp 1|3=Tipp 1 verbergen}} | {{Lösung versteckt|1=α und α' sind Stufenwinkel. Wie groß ist dann α'?|2=Tipp 1|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1=β und β' sind Scheitelwinkel. Wie groß ist dann β?|2=Tipp 2|3=Tipp 2 verbergen}} | {{Lösung versteckt|1=β und β' sind Scheitelwinkel. Wie groß ist dann β?|2=Tipp 2|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=Berechne den fehlenden Winkel γ mithilfe des Innenwinkelsatzes!|2=Tipp 3|3=Tipp 3 verbergen}} | {{Lösung versteckt|1=Berechne den fehlenden Winkel γ mithilfe des Innenwinkelsatzes!|2=Tipp 3|3=Tipp 3 verbergen}} | ||
{{Lösung versteckt|1=[[Datei:Lösung 2.3 lilaa.png|zentriert|rahmenlos| | {{Lösung versteckt|1=[[Datei:Lösung 2.3 lilaa.png|zentriert|rahmenlos|600x600px]]|2=Lösung|3=Lösung verbergen}}| Arbeitsmethode}} | ||
== Aufgabe 3 == | == Aufgabe 3 == | ||
{{LearningApp|width=100%|height=500px|app=22690980}} | {{LearningApp|width=100%|height=500px|app=22690980}} | ||
== Aufgabe 4 (Sicherung) == | == Aufgabe 4 (Sicherung) == | ||
{{LearningApp|width=100%|height=500px|app=25228963}} | {{LearningApp|width=100%|height=500px|app=25228963}} | ||
Version vom 14. November 2024, 11:50 Uhr
Informationskästchen
Einführung
Stimmt das auch wirklich?
Wenn ja, dann müssten die drei Innenwinkel im Dreieck einen gestreckten Winkel ergeben.
Das sollte dann also in etwa so aussehen:
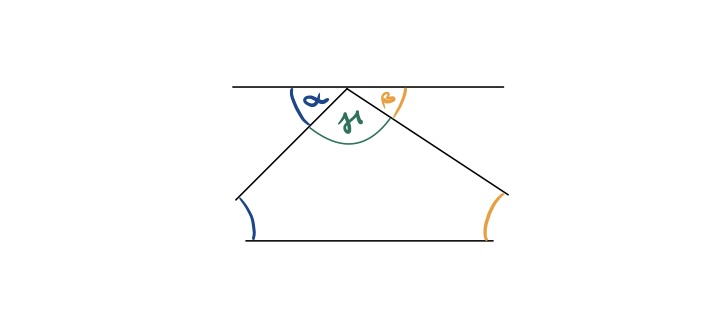
Reiße die zwei Winkel α und β deines Dreiecks (auf dem Arbeitsblatt) ab und prüfe, ob man sie an der Spitze zu einem gestreckten Winkel mit 180° anordnen kann.
Aufgabe 1
siehe Arbeitsblatt
Aufgabe 2
Aufgabe 3
Aufgabe 4 (Sicherung)