Benutzer:Anne Uni MS-14/Testseite: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Box|Merksätze|{{Lösung versteckt|1=[[Datei:Scheitelwinkel.jpg|rechts|200x200px]] | |||
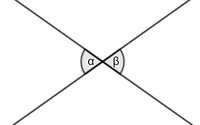
An zwei Geraden, die sich schneiden, nennt man gegenüberliegende Winkel '''Scheitelwinkel'''. Die Winkel sind gleich groß. | |||
In der Abbildung: α und β sind Scheitelwinkel und es gilt α <math>=</math> β. |2=Merksatz Scheitelwinkel|3=Merksatz Scheitelwinkel verbergen}}{{Lösung versteckt|1=[[Datei:Nebenwinkel.jpg|rechts|130x130px]] | |||
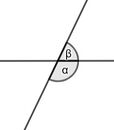
An zwei Geraden, die sich schneiden, nennt man nebeneinanderliegende Winkel '''Nebenwinkel'''. Nebenwinkel ergeben zusammen 180°. | |||
In der Abbildung: α und β sind Nebenwinkel und es gilt α+β <math>=</math> 180°.|2=Merksatz Nebenwinkel|3=Merksatz Nebenwinkel verbergen}} | |||
{{Lösung versteckt|1=[[Datei:Stufenwinkel.jpg|rechts|200x200px]] | |||
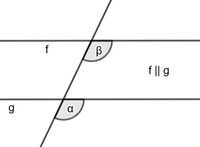
An zwei parallelen Geraden, die von einer weiteren Geraden geschnitten werden, nennt man Winkel, die in Stufen angeordnet sind, '''Stufenwinkel'''. | |||
Die Winkel sind gleich groß. | |||
In der Abbildung: α und β sind Stufenwinkel und es gilt α<math>=</math> β.|2=Merksatz Stufenwinkel|3=Merksatz Stufenwinkel verbergen}}{{Lösung versteckt|1=[[Datei:Wechselwinkel.jpg|rechts|180x180px]] | |||
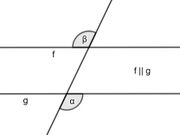
An zwei parallelen Geraden, die von einer weiterer Geraden geschnitten werden, erhält man '''Wechselwinkel''', indem man erst den Stufenwinkel und anschließend davon den Scheitelwinkel nimmt. Auch für Wechselwinkel gilt, dass sie gleich groß sind. | |||
In der Abbildung: α und β sind Wechselwinkel und es gilt α<math>=</math> β.|2=Merksatz Wechselwinkel|3=Merksatz Wechselwinkel verbergen}}|Merksatz | |||
}} | |||
{{Box|Merksatz: Nebenwinkel|{{Lösung versteckt|1=[[Datei:Nebenwinkel.jpg|rechts|130x130px]] | |||
An zwei Geraden, die sich schneiden, nennt man nebeneinanderliegende Winkel '''Nebenwinkel'''. Nebenwinkel ergeben zusammen 180°. | |||
In der Abbildung: α und β sind Nebenwinkel und es gilt α+β <math>=</math> 180°.|2=Merksatz|3=Merksatz verbergen}}|Merksatz | |||
}} | |||
{{Box|Merksatz: Stufenwinkel|{{Lösung versteckt|1=[[Datei:Stufenwinkel.jpg|rechts|200x200px]] | |||
An zwei parallelen Geraden, die von einer weiteren Geraden geschnitten werden, nennt man Winkel, die in Stufen angeordnet sind, '''Stufenwinkel'''. | |||
Die Winkel sind gleich groß. | |||
In der Abbildung: α und β sind Stufenwinkel und es gilt α<math>=</math> β.|2=Merksatz|3=Merksatz verbergen}}|Merksatz | |||
}} | |||
{{Box|Merksatz: Wechselwinkel|{{Lösung versteckt|1=[[Datei:Wechselwinkel.jpg|rechts|180x180px]] | |||
An zwei parallelen Geraden, die von einer weiterer Geraden geschnitten werden, erhält man '''Wechselwinkel''', indem man erst den Stufenwinkel und anschließend davon den Scheitelwinkel nimmt. Auch für Wechselwinkel gilt, dass sie gleich groß sind. | |||
In der Abbildung: α und β sind Wechselwinkel und es gilt α<math>=</math> β.|2=Merksatz|3=Merksatz verbergen}}|Merksatz | |||
}} | |||
{{Box|Merksatz: Scheitelwinkel|{{Lösung versteckt|1=[[Datei:Scheitelwinkel.jpg|rechts|200x200px]] | {{Box|Merksatz: Scheitelwinkel|{{Lösung versteckt|1=[[Datei:Scheitelwinkel.jpg|rechts|200x200px]] | ||
| Zeile 40: | Zeile 91: | ||
Einen neuen Absatz beginnt man in der Quelltextbearbeitung durch zwei aufeinanderfolgende Zeilenumbrüche, also einer leeren Zeile zwischen den beiden Absätzen. In der visuellen Bearbeitung reicht hierzu das einmalige Betätigen der Eingabetaste. | Einen neuen Absatz beginnt man in der Quelltextbearbeitung durch zwei aufeinanderfolgende Zeilenumbrüche, also einer leeren Zeile zwischen den beiden Absätzen. In der visuellen Bearbeitung reicht hierzu das einmalige Betätigen der Eingabetaste. | ||
===Vorlagen === | ===Vorlagen=== | ||
{{Lösung versteckt|Das ist ein Tipp|Tipp anzeigen|Tipp verbergen}}{{Lösung versteckt|Das ist eine Lösung|Lösung anzeigen|Lösung verbergen}}{{Box|Aufgabe 1: Münzwurf|Inhalt|Arbeitsmethode | {{Lösung versteckt|Das ist ein Tipp|Tipp anzeigen|Tipp verbergen}}{{Lösung versteckt|Das ist eine Lösung|Lösung anzeigen|Lösung verbergen}}{{Box|Aufgabe 1: Münzwurf|Inhalt|Arbeitsmethode | ||
}}{{Box|Merksatz: Kongruenzsätze|Inhalt|Merksatz | }}{{Box|Merksatz: Kongruenzsätze|Inhalt|Merksatz | ||
| Zeile 46: | Zeile 97: | ||
}} | }} | ||
===Dateien=== | ===Dateien=== | ||
====Über die Bedienelemente==== | ====Über die Bedienelemente ==== | ||
[[Datei:Monty Hall. Ilustración de paradoja. Puerta abierta.png|mini|rechts|Ziegenproblem]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | [[Datei:Monty Hall. Ilustración de paradoja. Puerta abierta.png|mini|rechts|Ziegenproblem]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | ||
====Mittels Quelltexteingabe (Ohne Umfließen des Textes)==== | ====Mittels Quelltexteingabe (Ohne Umfließen des Textes)==== | ||
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.[[Datei:GIF Basketball.gif|mini|ohne|Ballwurf]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.[[Datei:GIF Basketball.gif|mini|ohne|Ballwurf]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | ||
====Über Wikipedia (Ohne Rahmen) ==== | ====Über Wikipedia (Ohne Rahmen)==== | ||
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.[[File:KreisMittelpunktRadius.svg|rahmenlos|ohne|500px]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.[[File:KreisMittelpunktRadius.svg|rahmenlos|ohne|500px]]Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. | ||
===Interaktive Applets=== | ===Interaktive Applets=== | ||
====LearningApp==== | ====LearningApp==== | ||
{{LearningApp|width=100%|height=600px|app=phcsyj21c17}} | {{LearningApp|width=100%|height=600px|app=phcsyj21c17}} | ||
==== GeoGebra ==== | ====GeoGebra==== | ||
<ggb_applet id="cDyjWjkp" width="100%" height="100%" /> | <ggb_applet id="cDyjWjkp" width="100%" height="100%" /> | ||
==Kombinationen == | ==Kombinationen== | ||
Die Inhalte basieren auf dem Lernpfad [https://unterrichten.zum.de/wiki/Quadratische_Funktionen_erkunden Quadratische Funktionen erkunden] von [[Benutzer:Elena Jedtke|Elena Jedtke]]. | Die Inhalte basieren auf dem Lernpfad [https://unterrichten.zum.de/wiki/Quadratische_Funktionen_erkunden Quadratische Funktionen erkunden] von [[Benutzer:Elena Jedtke|Elena Jedtke]]. | ||
{{Box|Merksatz: Quadratische Funktionen|Quadratische Funktionen können in der Form <math>f(x)=a(x-{\color{blue}d})^2+{\color{green}e}</math> angegeben werden (wobei <math>a \neq 0</math>). Diese Darstellungsform nennt man '''Scheitelpunktform''', da sich der Scheitelpunkt direkt ablesen lässt. Er hat die Koordinaten <math>S({\color{blue}d}|{\color{green}e})</math>.|Merksatz | {{Box|Merksatz: Quadratische Funktionen|Quadratische Funktionen können in der Form <math>f(x)=a(x-{\color{blue}d})^2+{\color{green}e}</math> angegeben werden (wobei <math>a \neq 0</math>). Diese Darstellungsform nennt man '''Scheitelpunktform''', da sich der Scheitelpunkt direkt ablesen lässt. Er hat die Koordinaten <math>S({\color{blue}d}|{\color{green}e})</math>.|Merksatz | ||
| Zeile 170: | Zeile 221: | ||
</div> | </div> | ||
=== Navigation=== | ===Navigation=== | ||
<span style="color: red">Parameter ''vorherlink'' an aktuellen Lernpfad anpassen.</span> | <span style="color: red">Parameter ''vorherlink'' an aktuellen Lernpfad anpassen.</span> | ||
| Zeile 207: | Zeile 258: | ||
</div> | </div> | ||
===Kategoriezuordnung === | ===Kategoriezuordnung=== | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 221: | Zeile 272: | ||
</div> | </div> | ||
===Aufgaben-Boxen=== | === Aufgaben-Boxen=== | ||
====Schwierigkeitsstufe I==== | ====Schwierigkeitsstufe I==== | ||
| Zeile 236: | Zeile 287: | ||
</div> | </div> | ||
====Schwierigkeitsstufe II==== | ==== Schwierigkeitsstufe II==== | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 262: | Zeile 313: | ||
</div> | </div> | ||
====Mit Verweis zum Arbeitsblatt==== | ==== Mit Verweis zum Arbeitsblatt==== | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2"> | <div class="width-1-2"> | ||
| Zeile 276: | Zeile 327: | ||
</div> | </div> | ||
====LK-Kennzeichnung==== | ====LK-Kennzeichnung ==== | ||
=====Gesamte Aufgabe===== | =====Gesamte Aufgabe===== | ||
| Zeile 318: | Zeile 369: | ||
===Andere Boxen=== | ===Andere Boxen=== | ||
====Merksatz==== | ====Merksatz ==== | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 331: | Zeile 382: | ||
</div> | </div> | ||
==== Beispiel ==== | ====Beispiel==== | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 344: | Zeile 395: | ||
</div> | </div> | ||
===Eingebettete Aufgabenstellung=== | ===Eingebettete Aufgabenstellung === | ||
<div class="grid"> | <div class="grid"> | ||
Version vom 10. November 2024, 10:34 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger, funktioniert aber über die Quelltextbearbeitung.
Einen neuen Absatz beginnt man in der Quelltextbearbeitung durch zwei aufeinanderfolgende Zeilenumbrüche, also einer leeren Zeile zwischen den beiden Absätzen. In der visuellen Bearbeitung reicht hierzu das einmalige Betätigen der Eingabetaste.
Vorlagen
Dateien
Über die Bedienelemente
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum. Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Mittels Quelltexteingabe (Ohne Umfließen des Textes)
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Über Wikipedia (Ohne Rahmen)
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisici elit, sed eiusmod tempor incidunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquid ex ea commodi consequat. Quis aute iure reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint obcaecat cupiditat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
Interaktive Applets
LearningApp
GeoGebra

Kombinationen
Die Inhalte basieren auf dem Lernpfad Quadratische Funktionen erkunden von Elena Jedtke.
Auf dieser Seite sind verschiedene Vorlagen für die Lernpfadkapitel des Seminars Digitale Werkzeuge in der Schule dargestellt. Dabei findet sich jeweils links im grau unterlegten Feld der benötigte Code um die Ausgabe rechts daneben zu erhalten.
Allgemeines
Kapitel-Informationskästchen
Bei Lernpfaden für die Sekundarstufe I oder Einführungsphase entfällt der Stichpunkt zu LK-Aufgaben!
{{Box
|1=Info
|2=In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>
Für die Bearbeitung dieses Kapitels benötigst du den Hefter [https://projekte.zum.de/wiki/Datei:Hefter_zum_Lernpfad_Pyramiden_entdecken.pdf "Pyramiden entdecken"], einen Taschenrechner, einen Stift, einen Bleistift, vier verschiedenfarbige Stifte, einen Zirkel, ein Geodreieck, ein Lineal (mind. 7 cm lang), eine Schere, etwas Klebeband, zwei lose DIN A3-Blätter und zwei lose DIN A4-Blätter.
Bei den Aufgaben unterscheiden wir folgende Typen:
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen.
* Aufgaben in '''<span style="color: #CD2990">pinker</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''.
* Und Aufgaben mit '''<span style="color: #5E43A5">lilanem</span>''' Streifen sind '''Knobelaufgaben'''.
* Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Viel Erfolg!
|3=Kurzinfo}}
Parameter vorherlink an aktuellen Lernpfad anpassen.
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/LERNPFAD#Kapitelauswahl}}
Parameter weiterlink an aktuellen Lernpfad anpassen.
{{Fortsetzung|weiter=weiter zum nächsten Kapitel|weiterlink=Digitale_Werkzeuge_in_der_Schule/LERNPFAD#Kapitel}}
{{Lösung versteckt|1=Inhalt|2=Lösung|3=Lösung verbergen}}
Kategoriezuordnung
{{SORTIERUNG:{{SUBPAGENAME}}}}
[[Kategorie:Digitale Werkzeuge in der Schule]]
Siehe Kategorie am Ende dieser Seite.
Aufgaben-Boxen
Schwierigkeitsstufe I
{{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode | Farbe={{Farbe|orange}} }}
Schwierigkeitsstufe II
{{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode | Farbe=#CD2990 }}
Schwierigkeitsstufe III
{{Box | Aufgabe <Nummer>: <Name> | Inhalt | Arbeitsmethode}}
Mit Verweis zum Arbeitsblatt
{{Box | Aufgabe <Nummer>: <Name> |
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt'''
| Arbeitsmethode | Farbe={{Farbe|orange}} }}
LK-Kennzeichnung
Gesamte Aufgabe
{{Box | Aufgabe <Nummer>⭐: <Name> | Inhalt | Arbeitsmethode}}
Teilaufgabe
{{Box | Aufgabe <Nummer>: <Name> |
'''a)''' Inhalt
'''b)''' Inhalt
'''c)⭐''' Inhalt
| Arbeitsmethode}}
Andere Boxen
Merksatz
{{Box | Merksatz: <Name> | Inhalt | Merksatz | Farbe={{Farbe|grün|dunkel}}}}
Beispiel
{{Box | Beispiel: <Name> | Inhalt | Hervorhebung1}}
Eingebettete Aufgabenstellung
<div style="background:#FFFACD; border:ridge #FFEC8B; padding:10px"> Hier steht eine eingebettete Aufgabenstellung. </div>
Hier steht eine eingebettete Aufgabenstellung.
Applets
Technischer Benutzungshinweis
[[Datei:About icon (The Noun Project).svg|15px|middle]] Technischer Benutzungshinweis
Mathematik-Modus
Äquivalenzumformung
<math>\begin{align}
& & x^2 + 24 &= 42 - 0 & &\mid \text{Termumformung}\\
\Leftrightarrow & & x^2 + 24 &= 42 & &\mid -24\\
\Leftrightarrow & & x^2 &= 18 & &\mid \pm \surd\\
\Leftrightarrow & & x &= \pm \sqrt{18}
\end{align}</math>
Gleichungskette
<math>\begin{align}
A_{\text{Kreis}} &= \pi \cdot r^2\\
&= \pi \cdot 42^2\\
&= \pi \cdot 1.764^2\\
&\approx 5.541{,}7
\end{align}</math>
LGS
<math>\begin{array}{crcrcr}\\
\text{I}\quad & 7x & - & 2y & = & 48\\
\text{II}\quad & 3x & + & 11y & = & 11
\end{array}</math>
<math>\left\vert\begin{alignat}{7}
x &&\; + \;&& 42y &&\; - \;&& z &&\; = \;&& 1 \\
4242x &&\; - \;&& 24y &&\; + \;&& 4z &&\; = \;&& -42\\
-x &&\; + \;&& \tfrac{1}{3} y &&\; \;&& &&\; = \;&& 0
\end{alignat}\right\vert</math>
Vektoren und Matrizen
<math>\begin{pmatrix}
1\\
2\\
3
\end{pmatrix}</math>
<math>\begin{pmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{pmatrix}</math>
Mit Text in einer Zeile geht <math>\left( \begin{smallmatrix}
1\\
2\\
3
\end{smallmatrix} \right)</math> so und <math>\left( \begin{smallmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{smallmatrix} \right)</math> so.
Mit Text in einer Zeile geht so und so.