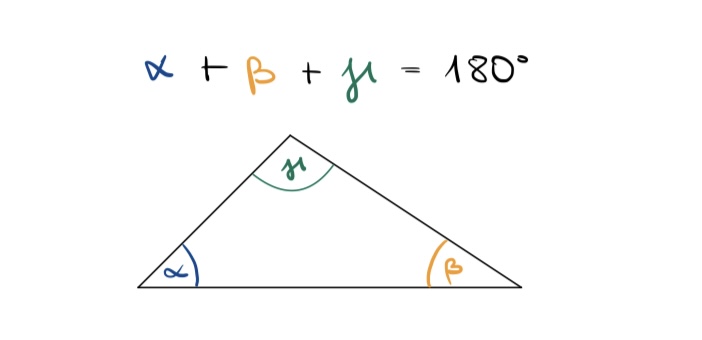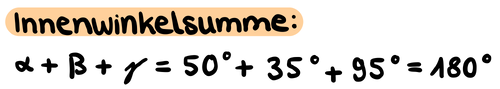Geometrie im Dreieck/Geheimcode der Geometrie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 4: | Zeile 4: | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die | * In Aufgaben, die <span style="color:orange"'''orange'''> gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | ||
* Aufgaben in '''pinker''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | * Aufgaben in '''pinker''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | ||
* Und Aufgaben mit '''lilanem''' Streifen sind '''schwierige Aufgaben'''. | * Und Aufgaben mit '''lilanem''' Streifen sind '''schwierige Aufgaben'''. | ||
Version vom 8. November 2024, 09:34 Uhr
Informationskästchen
Einführung
Stimmt das auch wirklich?
Wenn ja, dann müssten die drei Innenwinkel im Dreieck einen gestreckten Winkel ergeben.
Das sollte dann also in etwa so aussehen:
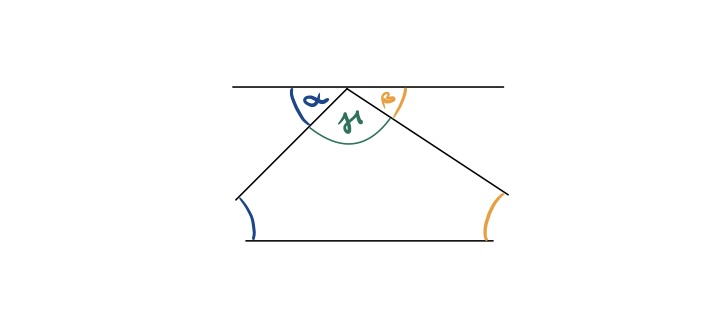
Reiße die zwei Winkel α und β deines Dreiecks (auf dem Arbeitsblatt) ab und prüfe, ob man sie an der Spitze zu einem gestreckten Winkel mit 180° anordnen kann.
Aufgabe 1
siehe Arbeitsblatt
Aufgabe 2
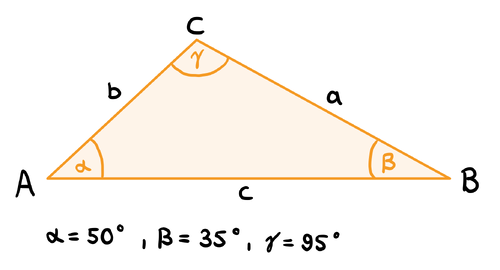
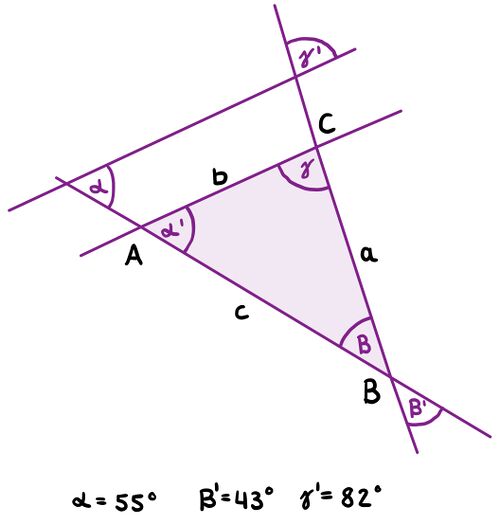
Addiere alle drei Innenwinkel, um die Innenwinkelsumme zu berechnen.
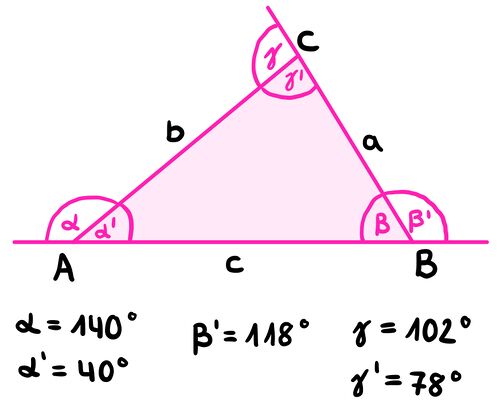
Überlege zunächst, was die Innenwinkel und was die Außenwinkel sind.
Beta und Beta' sind Nebenwinkel. Wie kannst du herausfinden, wie groß Beta ist?
Alpha ist der Stufenwinkel zu Alpha'.
Beta ist der Scheitelwinkel zu Beta'.
Gamma ist der Wechselwinkel zu Gamma'.
Aufgabe 3
Aufgabe 4 (Sicherung)