Abitur Physik am Gymnasium Trittau/Doppelspalt: Unterschied zwischen den Versionen
GT062 (Diskussion | Beiträge) |
GT062 (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
==Experiment Doppelspalt== | ==Experiment Doppelspalt== | ||
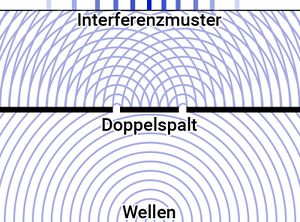
Ein Doppelspalt sind zwei parallele Einzelpalte und somit auch ein 2-maschiges Gitter. Nun wird Licht durch den Doppelspalt geschickt. Wenn das Licht den Doppelspalt passiert hat, beugt es sich in die Schattenräume und destruktive sowie konstruktive Interferenz findet statt. Diese Interferenzen werden nun anhand des auf dem Schirm abgebildeten Interferenzmuster visualisiert. | Ein Doppelspalt sind zwei parallele Einzelpalte und somit auch ein 2-maschiges Gitter. Nun wird Licht durch den Doppelspalt geschickt. Wenn das Licht den Doppelspalt passiert hat, beugt es sich durch Elementarwellen in die Schattenräume und destruktive sowie konstruktive Interferenz findet statt. Diese Interferenzen werden nun anhand des auf dem Schirm abgebildeten Interferenzmuster visualisiert. | ||
[[Datei:Interferenzmuster-Doppelspalt.jpg|links|mini]] | [[Datei:Interferenzmuster-Doppelspalt.jpg|links|mini]] | ||
Auf dem Schirm zu erkennen sind nun | Auf dem Schirm zu erkennen sind nun Lichtstreifen, die sogenannten Maxima. Sie kennzeichnen einen Bereich der konstruktiven Interferenz. Das stärkste Maximum welches den geringsten Abstand zur Spaltmitte aufweist ist das Hauptmaximum oder auch 0. Maximum genannt. Die zweitstärksten Maxima sind dann die 1. Maxima. Die freien Flächen zwischen den Maxima sind die Minima. | ||
für Maxima: <math>\frac {n\times\lambda}{b}=\sin (a_n)= \frac {(s_n)}{(e_n)}</math> | |||
für Minima: <math>\frac {2n+1}{2b}\times\lambda\approx\sin(a_n)=\frac{s_n}{e_n}</math> | |||
Version vom 20. Februar 2024, 11:02 Uhr
Experiment Doppelspalt
Ein Doppelspalt sind zwei parallele Einzelpalte und somit auch ein 2-maschiges Gitter. Nun wird Licht durch den Doppelspalt geschickt. Wenn das Licht den Doppelspalt passiert hat, beugt es sich durch Elementarwellen in die Schattenräume und destruktive sowie konstruktive Interferenz findet statt. Diese Interferenzen werden nun anhand des auf dem Schirm abgebildeten Interferenzmuster visualisiert.
Auf dem Schirm zu erkennen sind nun Lichtstreifen, die sogenannten Maxima. Sie kennzeichnen einen Bereich der konstruktiven Interferenz. Das stärkste Maximum welches den geringsten Abstand zur Spaltmitte aufweist ist das Hauptmaximum oder auch 0. Maximum genannt. Die zweitstärksten Maxima sind dann die 1. Maxima. Die freien Flächen zwischen den Maxima sind die Minima.
für Maxima:
für Minima:
Berechnung des Doppelspaltes
Tafelwerk: S.131
Metzler: S.302; 386; 392