Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 53: | Zeile 53: | ||
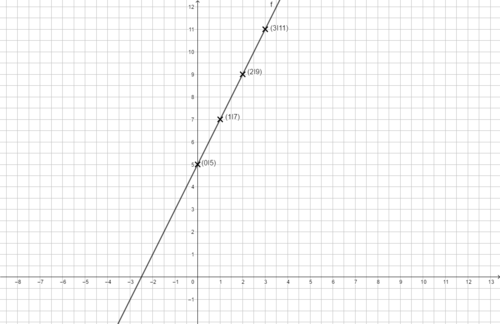
[[Datei:F(x)=2x+5 mit Punkten.png|rahmenlos|500x500px]] | [[Datei:F(x)=2x+5 mit Punkten.png|rahmenlos|500x500px]] | ||
|Kurzinfo}} | |Kurzinfo}} | ||
{{Lösung versteckt|1= | |||
{{ | |||
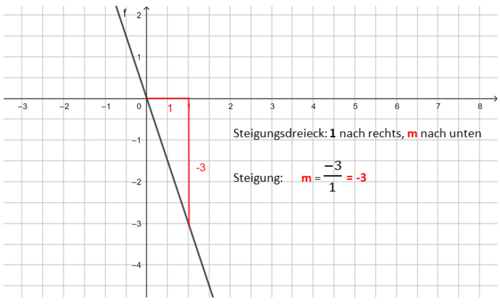
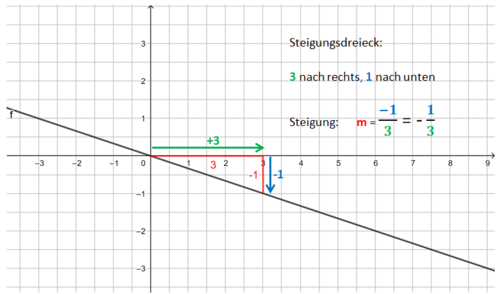
Beispiele:<br> | Beispiele:<br> | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 64: | Zeile 62: | ||
[[Datei:Steigungsdreieck m ganze Zahl (negativ).png|rahmenlos|500x500px]] | [[Datei:Steigungsdreieck m ganze Zahl (negativ).png|rahmenlos|500x500px]] | ||
{{LearningApp|app=p1e8uj53c21|width=100%|heigth=600px}}</div> | {{LearningApp|app=p1e8uj53c21|width=100%|heigth=600px}}</div> | ||
</div> | </div> | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 74: | Zeile 71: | ||
{{LearningApp|app=pqf5b16sj21|width=100%|heigth=600px}}</div> | {{LearningApp|app=pqf5b16sj21|width=100%|heigth=600px}}</div> | ||
</div> | </div> | ||
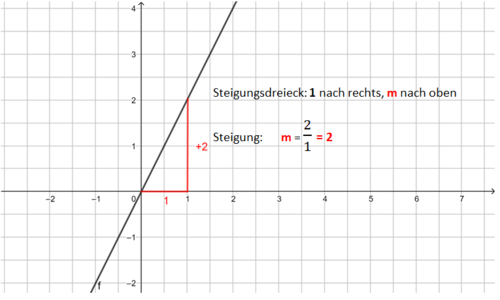
|2=Die Steigung mithilfe des Steigungsdreieckes bestimmen|3=Verbergen}} | |||
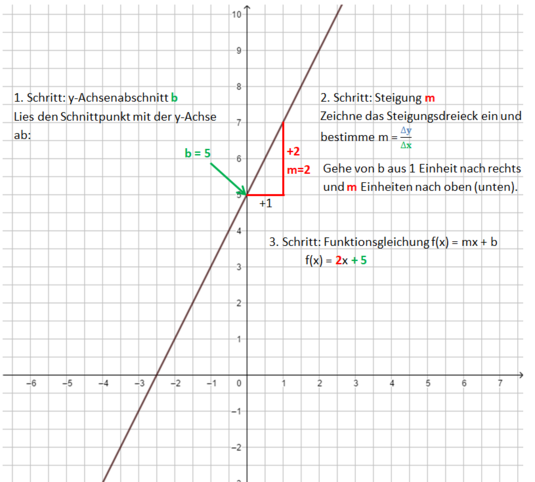
{{Box|Bestimmen der Funktionsgleichung einer Geraden|* Lies den y-Achsenabschnitt b ab. | |||
* Zeichne das Steigungsdreieck und bestimme damit die Steiung m.|Merksatz}} | |||
<div class="grid"> | |||
<div class="width-1-3">Beispiel 1 (leicht): m ist eine natürliche Zahl<br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=2.png|535x535px]]</div> | |||
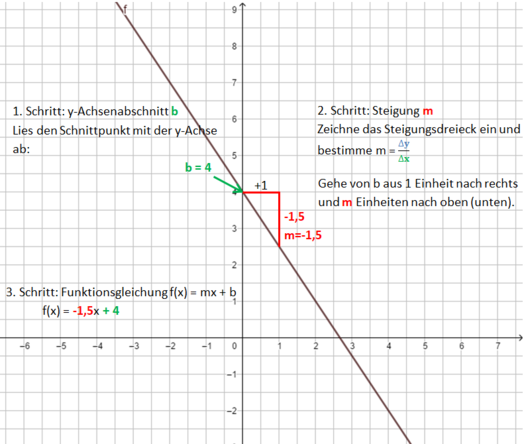
<div class="width-1-3">Beispiel 2 (mittel): m ist eine negative ganze Zahl <br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=-1,5.png|528x528px]]</div> | |||
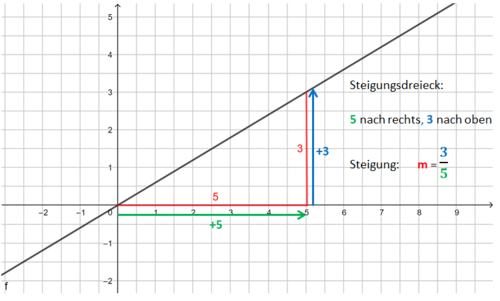
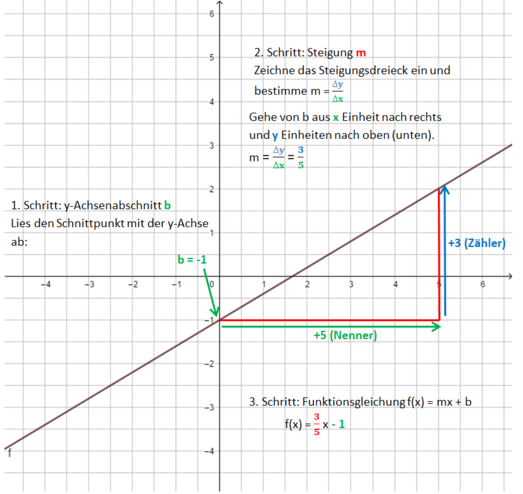
<div class="width-1-3">Beispiel 3 (schwer): m ist ein Bruch <br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=drei Fünftel.png|523x523px]]</div> | |||
</div> | |||
{{Box|Übung: Bestimmen der Funktionsgleichung einer Geraden|Ordne den Geraden die Funktionsgleichung zu. Wähle eine passende Schwierigkeit aus.|Üben}} | |||
<div class="grid"> | |||
<div class="width-1-3">leicht (*){{LearningApp|app=phd8q7we221|width=100%|height=400px}}{{LearningApp|app=p2rwidw3t20|width=100%|height=400px}}</div> | |||
<div class="width-1-3">mittel (**){{LearningApp|app=popvxxk2v21|width=100%|height=400px}}{{LearningApp|app=pw8bbo2st20|width=100%|height=400px}}</div> | |||
<div class="width-1-3">schwer (***){{LearningApp|app=p5mxjgbpt21|width=100%|height=400px}} | |||
{{LearningApp|app=ppn4q2oe320|width=100%|height=400px}}</div> | |||
<br> | |||
Version vom 29. Dezember 2022, 14:48 Uhr
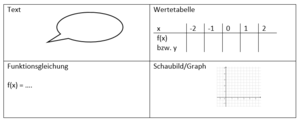
Funktionen
Lineare Funktionen
Diese Eigenschaften werden in folgendem Lied besungen.
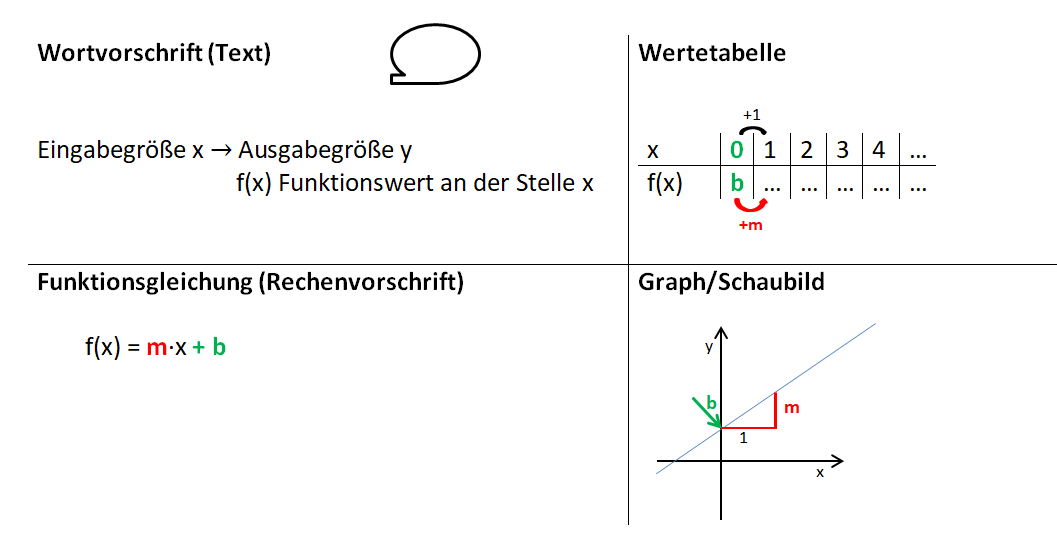
Hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen).
Beispiele:
leicht (*)
mittel (**)
schwer (***)