Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden verknüpfen

zurück zur Kapitelauswahl

Info

In diesem Lernpfadkapitel kannst du dein bereits erworbenes Wissen zum Thema Pyramiden vertiefen. Zudem lernst du mithilfe des Satzes von Pythagoras verschiedene Größen einer Pyramide zu berechnen.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den E-Kurs gedacht.

Viel Erfolg!

Checkliste - Das brauchst du

Checkliste

Für dieses Kapitel solltest du...

• die Oberfläche einer Pyramide berechnen können (siehe Kapitel Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen).

• den Satz des Pythagoras anwenden können.

Info

Falls du den Satz des Pythagoras noch einmal wiederholen möchtest, kannst du dein Wissen in Aufgabe 1 auffrischen.

Wenn du dich schon sicher im Umgang mit dem Satz des Pythagoras fühlst, kannst du direkt mit Aufgabe 2 fortfahren.

Satz des Pythagoras

Aufgabe 1: Wiederholung des Satzes von Pythagoras

a) Ergänze den Lückentext mit den bereits bekannten Begriffen des Satzes von Pythagoras.

Technischer Bedienungshinweis

Klicke zum Ausfüllen auf die Lücken und wähle aus den angegebenen Vorschlägen aus. Kontrolliere deine Lösung mit dem blauen Haken.

b) Berechne den Flächeninhalt des roten Quadrats.

Nutze für die Berechnung das Arbeitsblatt „Pyramiden verknüpfen“.

Tipp 1 zu b) anzeigen

Schau dir die Abbildung an. Kannst du die Abbildung auf die Aufgabe beziehen?

In diesem Beispiel gilt: $4^2 + 3^2 = 5^2$.

Tipp 2 zu b) anzeigen

Für den Flächeninhalt $A$ eines Quadrats mit der Seitenlänge $a$ gilt:

$A = a^2$.

Lösung zu b) anzeigen

$\begin{align} & & (4 \text{ cm})^2 + b^2 &= 21\text{ cm}^2 & &\mid - (4 \text{ cm})^2\\ \Leftrightarrow & & b^2 &= 21 \text{ cm}^2 - (4 \text{ cm})^2 \\ \Leftrightarrow & & b^2 &= 21 \text{ cm}^2 - 16 \text{ cm}^2 \\ \Leftrightarrow & & b^2 &= 5 \text{ cm}^2 \end{align}$

Der Flächeninhalt des roten Quadrats beträgt $5 \text{ cm}^2$.

Anwendungsaufgaben

Aufgabe 2: Sightseeing in Paris 1 - Der Louvre

Nutze für diese Aufgabe das Arbeitsblatt „Pyramiden verknüpfen“.

Glaspyramide im Innenhof des Louvre.

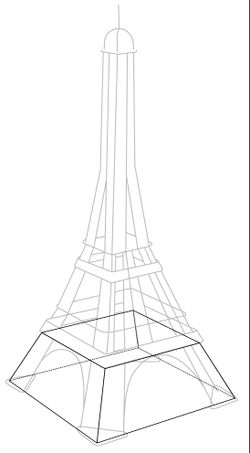
Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum Louvre teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche.

Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: „Wie lang sind die Edelstahlträger an den Seitenkanten der Pyramide?" Der Touristenführer weiß nur, dass die Pyramide 21 Meter hoch ist.

a) Beurteile, ob diese Angabe genügt, um die Länge eines Stahlträgers zu berechnen. Falls dem nicht so ist, gib Größen an, die zusätzlich benötigt werden.

b) Ein anderer Tourist findet im Internet eine Angabe zur Seitenlänge der quadratischen Grundfläche von 35 Metern. Berechne mithilfe der gegeben Größen die Länge eines Stahlträgers an der Seitenkante der Pyramide.

Tipp 1 zu b) anzeigen

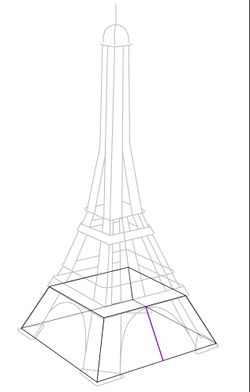
Zeichne zur Veranschaulichung eine passende Pyramide auf dein Arbeitsblatt.

Tipp 2 zu b) anzeigen

Du kannst zur Berechnung der gesuchten Seite den Satz des Pythagoras beliebig oft anwenden.

Tipp 3 zu b) anzeigen

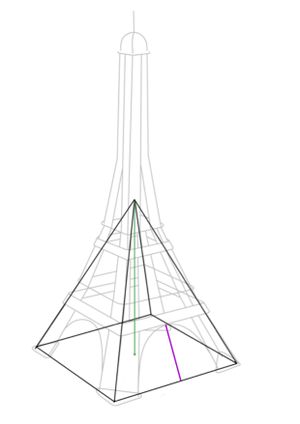
Überlege dir Hilfsdreiecke innerhalb der Pyramide, in denen du den Satz des Pythagoras anwenden kannst.

Tipp 4 zu b) anzeigen

Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen mögliche Hilfsdreiecke anzeigen lassen.

/>

Lösung zu b) anzeigen

Gegeben sind die Höhe der Pyramide mit $h=21~\mathrm{m}$ und die Seitenlänge der Grundfläche mit $a=35~\mathrm{m}$.
Du kannst verschiedene Kombinationen an Hilfsdreiecken nutzen, um die Länge eines Stahlträgers zu bestimmen.
Im Folgenden zeigen wir eine dieser Möglichkeiten.

Zunächst berechnen wir Diagonalenlänge $d_a$ der Pyramidengrundfläche mit Hilfe des Satzes des Pythagoras: $\begin{align} & & (35~\mathrm{m})^2+ (35~\mathrm{m})^2 &=d_a^2 & &\mid \text{Termumformung}\\ \Leftrightarrow & & 2450~\mathrm{m}^2 &=d_a^2 & &\mid \sqrt{} \\ \Leftrightarrow & & \sqrt{2450~\mathrm{m}^2} &=d_a & &\mid \text{Termumformung}\\ \Leftrightarrow & & 49{,}50~\mathrm{m} &\approx d_a & & \end{align}$

Nun betrachten wir das Dreieck bestehend aus der Seite $\frac{d_a}{2}$, der Höhe $h=21~\mathrm{m}$ der Pyramide und der Seitenkante $s$. Mithilfe des Satzes des Pythagoras lässt sich $s$ berechnen:

$\begin{align} & & \left(\frac{d_a}{2}\right)^2+ h^2 &=s^2 & &\mid \sqrt{}\\ \Leftrightarrow & & \sqrt{\left(\frac{d_a}{2}\right)^2+ h^2} &=s & &\mid \text{Werte einsetzen} \\ \Leftrightarrow & & \sqrt{\left(\frac{49{,}50~\text{m}}{2}\right)^2+ (21~\text{m})^2} &=s & &\mid \text{Termumformung}\\ \Leftrightarrow & & 32{,}46~\mathrm{m} &\approx s & & \end{align}$

Die Länge eines Stahlträgers der Pyramide beträgt demnach etwa $32{,}46~\mathrm{m}^2$.

c) Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen.

Tipp 1 zu c) anzeigen

Die Größe der Glasfläche entspricht der Mantelfläche der Pyramide.

Tipp 2 zu c) anzeigen

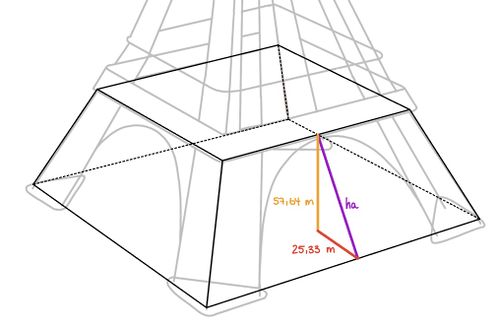
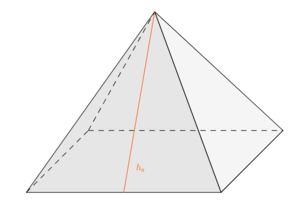
Verwende die berechnete Länge eines Stahlträgers aus Aufgabenteil b) und bestimme damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide.

Tipp 3 zu c) anzeigen

Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen verschiedene Hilfsdreiecke in der Pyramide anzeigen lassen. Suche das geeignete Hilfsdreieck, um die Seitenhöhe zu berechnen.

Lösung zu c) anzeigen

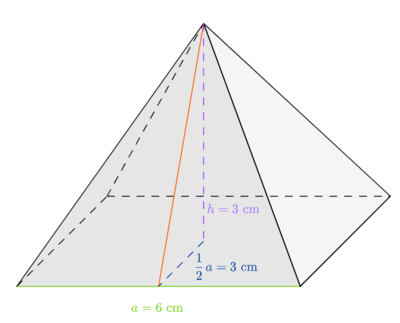
Es wird der Satz des Pythagroas auf das Dreieck, welches aus einer Seitenkante $s \approx 32{,}46~\mathrm{m}$ der Pyramide , der Höhe der Pyramidenseite $h_a$ und der Hälfte der Seitenlänge der Grundfläche $\frac{a}{2} = \frac{35~\mathrm{m}}{2}$ besteht, angewendet.
Damit folgt für die Höhe der Pyramidenseite $h_a$:

$\begin{align} & & h_a^2+ \left(\frac{35~\mathrm{m}}{2}\right)^2 &= s^2 & & \mid -\left(\frac{35~\mathrm{m}}{2}\right)^2 \\ \Leftrightarrow & & h_a^2 &= s - \left(\frac{35~\mathrm{m}}{2}\right)^2 & &\mid \sqrt{} \\ \Leftrightarrow & & h_a &= \sqrt{ s^2 - \left(\frac{35~\mathrm{m}}{2}\right)^2} & & \mid \text{Werte einsetzen} \\ \Leftrightarrow & & h_a &\approx \sqrt{ (32{,}46~\mathrm{m})^2 - (17{,}5~\mathrm{m})^2} & & \mid \text{Termumformung}\\ \Leftrightarrow & & h_a &\approx 27{,}34~\mathrm{m} & & \end{align}$

Die Fläche einer Glaswand $A_\text{Seitenfläche}$ wird wie folgt berechnet: $\begin{align} & & A_\text{Seitenfläche} &= h_a \cdot \frac{35~\mathrm{m}}{2} & & \mid \text{Werte einsetzen} \\ \Leftrightarrow & & A_\text{Seitenfläche} &\approx 27{,}34~\mathrm{m} \cdot 17{,}5~\mathrm{m} & &\mid \text{Termumformung} \\ \Leftrightarrow & & A_\text{Seitenfläche} &\approx 478{,}45~\mathrm{m}^2 & & \end{align}$

Die gesamte Glasfläche der Pyramide $M$ besteht aus vier identischen Glaswandflächen $A_\text{Seitenfläche} \approx 478{,}45~\mathrm{m}^2$: $\begin{align} & & M &= 4 \cdot A_\text{Seitenfläche} & & \mid \text{Werte einsetzen} \\ \Leftrightarrow & & M &\approx 4 \cdot 478{,}45~\mathrm{m}^2 & & \mid \text{Termumformung} \\ \Leftrightarrow & & M &\approx 1913{,}8~\mathrm{m}^2 & & \end{align}$

Damit besitzt eine Glaswand eine Fläche von etwa $478{,}45~\mathrm{m}^2$. Die gesamte Glasfläche der Pyramide beträgt demnach rund $1913{,}8~\mathrm{m}^2$.

d) Vergleiche deine Vorgehensweise in den Aufgabenteilen b) und c) hinsichtlich gemeinsamer Teilschritte? Markiere und benenne diese in deinen Aufzeichnungen.

Checkliste zur Bestimmung der Mantelfläche

In Aufgabe 2 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet und in Aufgabenteil 2d) auch schon angefangen, die dazu nötige Vorgehensweise zu beschreiben.

a) In dem folgenden Applet wird die allgemeine Vorgehensweise noch einmal zusammengefasst. Bringe die einzelnen Teilschritte in die richtige Reihenfolge.

b) zurück zum Arbeitsblatt

Übertrage die Checkliste auf das Arbeitsblatt „Pyramiden verknüpfen“.

Aufgabe 3 ⭐: Sightseeing in Paris 2 - Der Eiffelturm

Nutze für deine Berechnungen das Arbeitsblatt „Pyramiden verknüpfen“.

Eiffelturm

Als nächster Stopp steht der Eiffelturm auf eurer Liste.

Da momentan das Gerüst des Eiffelturms erneuert wird, dienen 4 Stützen in den Torbögen als Stabilisierung. Du möchtest gerne wissen, wie lang diese Stützen sind. Dazu entnimmst du einer Informationstafel am Eiffelturm einige wichtige Maße des Bauwerks und versuchst die Berechnung näherungsweise anhand einer Pyramide mit quadratischer Grundfläche durchzuführen.

Du hast anhand der Daten eine Skizze angefertigt und schätzt die Höhe der Pyramide (grün) auf 140m. Die Stützen hast du in deiner Zeichnung lila markiert.

Tipp 1 anzeigen

Schätze anhand der obigen Skizze des Eiffelturms die Breite der 1. Etage.

Tipp 2 anzeigen

Kannst du im Eiffelturm eine Pyramide entdecken?

Tipp 3 anzeigen

Der Eiffelturm besitzt bis zur 1. Etage die Form eines Pyramidenstumpfes. Den Pyramidenstumpf kann du der unten stehenden Skizze entnehmen. Überlege dir anhand der Skizze welche Größen du schon kennst und welche Größen du noch bestimmen musst.

Tipp 4 anzeigen

Zur Berechnung des Flächeninhalts eines Trapezes benötigst du die Seitenhöhe des Pyramidenstumpfes. Die Seitenhöhe entspricht der lila Strecke in der unterstehenden Skizze. Konstruiere ein passendes Hilfsdreieck und wende den Satz des Pythagoras an.

Tipp 5 anzeigen

Der Flächeninhalt $A_T$ eines Trapezes wird über die folgende Formel berechnet: $A_T= \frac{1}{2} (a+c) \cdot h$.

Lösung anzeigen

Die Breite der ersten Etage kann anhand der Breite des Torbogens auf $74{,}24 ~\text{m}$ geschätzt werden. Die Länge eines Fußes des Eiffelturms wird über die folgende Gleichung bestimmt: $\text{Länge Fuß} = (124{,}90 ~\text{m} - 74{,}24 ~\text{m}):2$. Die Seitenhöhe $h_a$ des Trapezes wird über den Satz des Pythagoras bestimmt. Es gilt: $h_a^2=(57{,}64)^2 + (25{,}33)^2$ $h_a^2=(57{,}64)^2 + (25{,}33)^2$

$\begin{align} & & h_a^2=(57{,}64 ~\text{m})^2 + (25{,}33 ~\text{m})^2 & &\mid \sqrt{} \\ \Leftrightarrow & & h_a=\sqrt{(57{,}64 ~\text{m})^2 + (25{,}33 ~\text{m})^2} \\ \Leftrightarrow & & h_a \approx 62{,}96 ~\text{m} \\ \end{align}$

Aufgabe 4 ⭐: Der Würfel

Nutze für diese Aufgabe das Arbeitsblatt „Pyramiden verknüpfen“.

Der unten abgebildete Würfel lässt sich aus 6 regelmäßigen, gleichartigen Pyramiden zusammensetzen.

a) Beschreibe wie sich der Würfel aus den Pyramiden zusammensetzen lässt und wie diese Pyramiden aussehen.

Tipp 1 zu a) anzeigen

Überlege dir eine naheliegende Form für die Grundfläche der Pyramiden.

Tipp 2 zu a) anzeigen

Die Seitenfläche des Würfels entspricht der quadratischen Grundfläche der Pyramiden.

Tipp 3 zu a) anzeigen

Schau dir das Applet an und setze Haken an den verschieden nummerierten Pyramiden, indem du in die leeren Kästchen klickst. Du siehst nun wie die jeweilige Pyramide in dem Würfel liegt und wie alle Pyramiden ihn zusammen ausfüllen.

Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht?

Lösung zu a) anzeigen

Hast du als Lösung eine Zeichnung angefertigt, dann sollte diese ungefähr so aussehen:

Es ist auch eine Möglichkeit das Aussehen der Pyramiden und die Lage der 6 Pyramiden im Würfel mit Worten zu beschreiben. Dies könnte wie folgt lauten:

Die Pyramiden besitzen eine quadratische Grundfläche mit einer Seitenlänge von 6 cm und sind symmetrisch.

Der Würfel lässt sich aus 6 solchen Pyramiden zusammensetzen, indem die Seitenflächen des Würfels die Grundflächen der Pyramiden darstellen. Die Spitzen der 6 Pyramiden treffen sich im Mittelpunkt des Würfels.

b) Welche Höhe hat die Pyramide?

Tipp 1 zu b) anzeigen

Sieh dir noch einmal den Tipp 3 in Teilaufgabe a) ganz genau an.

Lösung zu b) anzeigen

Die Spitzen der Pyramiden treffen sich im Mittelpunkt des Würfels. Somit sind zwei Pyramiden, die aufeinander stehen, genauso hoch wie der Würfel ($6~\text{cm}$). Daraus ergibt sich, dass die Pyramiden eine Höhe von $3~\text{cm}$ haben.

c) Berechne die Länge der orange markierten Strecke $h_a$. Runde dabei auf 2 Nachkommastellen genau.

Tipp 1 zu c) anzeigen

Anhand des Würfels und der gegebenen Seitenlänge $a$ kannst du alle Größen herausfinden, die du zur Berechnung benötigst. Du brauchst die Seitenlänge der Grundfläche, sowie die Höhe der Pyramide.

Tipp 2 zu c) anzeigen

Du benötigst den Satz des Pythagoras zur Berechnung der Länge der Seite $h_a$ .

Lösung zu c) anzeigen

Mit Hilfe des Satzes des Pythagoras ergibt sich die folgende Formel:

$(h_a)^2=h^2+\biggl(\frac{1}{2}\cdot a\biggr)^2$.

Setzen wir nun, die uns bekannten Werte für $h$ und $a$ ein, so erhalten wir: $\begin{align} & & h_a^2 &= 3^2 + \left(\frac{1}{2}\cdot 6\right)^2 & & \mid \text{Termumformung} \\ \Leftrightarrow & & h_a^2 &= 3^2 + 3^2 & &\mid \text{Termumformung} \\ \Leftrightarrow & & h_a^2 &= 18 & & \mid \sqrt{} \\ \Leftrightarrow & & h_a &\approx 4{,}24 & & \end{align}$

Die orangene Strecke ist $4{,}24~\text{cm}$ lang.

zurück zur Kapitelauswahl