Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Addieren und Subtrahieren: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Bilder ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 97: | Zeile 97: | ||
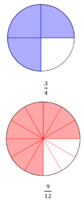
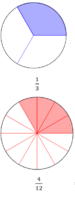
<div class="width-1-2">{{Lösung versteckt|Die Bruchteile sind nicht gleich groß. Welche Bruchteile kannst du für beide Brüche verwenden, um sie damit zu legen?|Tipp 1 zu b)|Schließen}} | <div class="width-1-2">{{Lösung versteckt|Die Bruchteile sind nicht gleich groß. Welche Bruchteile kannst du für beide Brüche verwenden, um sie damit zu legen?|Tipp 1 zu b)|Schließen}} | ||
{{Lösung versteckt|Lege die Brüche <math>\tfrac{3}{4}</math> und <math>\tfrac{1}{3}</math> jweils mit zwölftel Bruchteilen aus.<br> | {{Lösung versteckt|Lege die Brüche <math>\tfrac{3}{4}</math> und <math>\tfrac{1}{3}</math> jweils mit zwölftel Bruchteilen aus.<br> | ||
[[Datei:Drei Viertel gleich neun Zwölftel.png|rahmenlos]] [[Datei:Ein Drittel gleich vier Zwöftel.png|rahmenlos]]|Tipp 2 zu b)|Schließen}} | [[Datei:Drei Viertel gleich neun Zwölftel.png|rahmenlos|200x200px]] [[Datei:Ein Drittel gleich vier Zwöftel.png|rahmenlos|200x200px]]|Tipp 2 zu b)|Schließen}} | ||
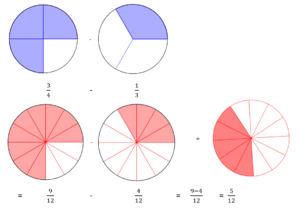
{{Lösung versteckt|[[Datei:Neun Zwöfltel minus vier Zölftel gleich fünf Zwölftel.png|rahmenlos]]|Lösung zu b)|Schließen}}</div> | {{Lösung versteckt|[[Datei:Neun Zwöfltel minus vier Zölftel gleich fünf Zwölftel.png|rahmenlos]]|Lösung zu b)|Schließen}}</div> | ||
</div> | </div> | ||
Version vom 28. Januar 2022, 17:36 Uhr
Addieren und Subtrahieren von Brüchen
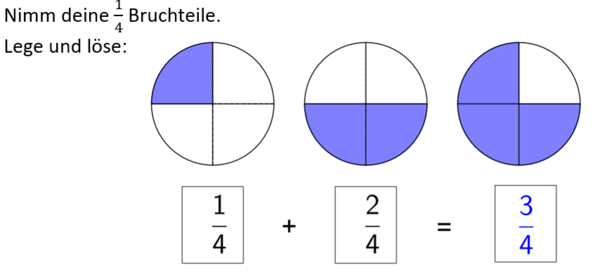
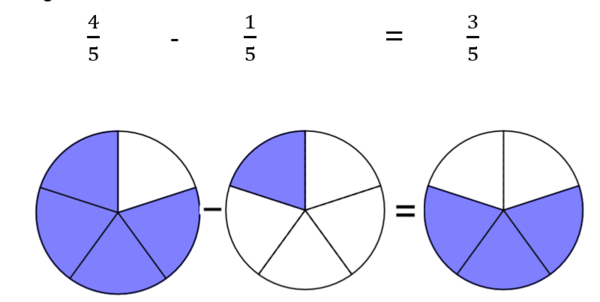
1 Addieren und subtrahieren gleichnamiger Brüche

Applet von GeoGebra Translation Team German
(direkter Link, falls die Darstellung schlecht ist: https://www.geogebra.org/m/mKDqMQAb )
Hier Fotos von Lösungen der Schüler sammeln und einfügen...
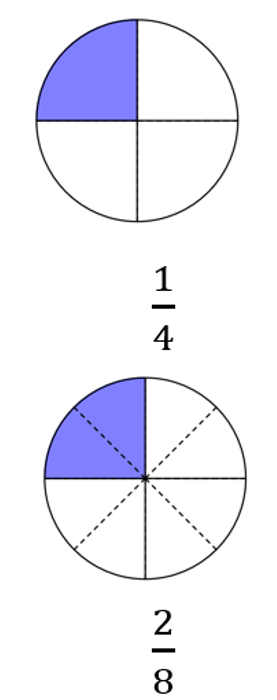
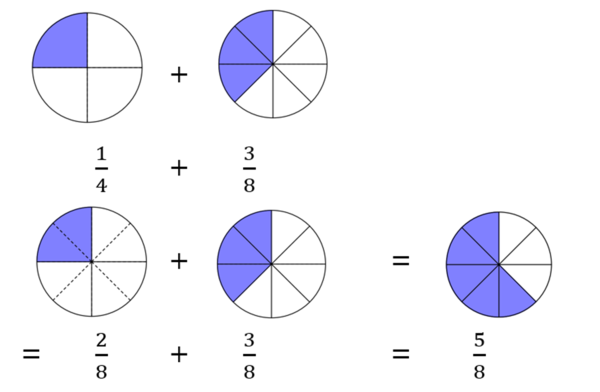
2 Addieren und Subtrahieren ungleichnamiger Brüche
Die Teile sind nicht gleich groß, die Brüche sind nicht gleichnamig. Kannst du statt der Viertel-Bruchteile den Bruch auch mit anderen Bruchteilen legen?
Ideensammlung: Rechnen mit Brüchen auf der Seite matheaufgabennet https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Bruchrechnung